Matrices and Calculus: Unit I: Matrices
Eigen Values and Eigen Vectors
Definition, Properties, Worked Examples
The word 'eigen' is German, which means 'characteristic' or 'proper'. So, an eigen value is also known as characteristic root or proper value. Sometimes it is also known as latent root.
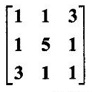
EIGEN VALUES AND EIGEN VECTORS Definition 1.2.1 Let A be a square matrix of order n. A number λ is called an eigen value of A if there exists a non-zero column matrix X such that AX = λX. Then X is called an eigen vector of A corresponding to λ. ⸫ the determinant of coefficients | A - λ I | = 0. This equation is called the characteristic equation of A. The determinant | A - λ I |, on expansion, will be a nth degree polynomial in λ and is known as the characteristic polynomial of A. The roots of the characteristic equation are the eigen values of A. Definition 1.2.2 Characteristic equation and characteristic polynomial If λ is a characteristic root of a square matrix A, then | A - λ I | = 0 is called the characteristic equation of A. The polynomial | A - λ I | in λ is called the characteristic polynomial of A. Note (1) The word 'eigen' is German, which means 'characteristic' or 'proper'. So, an eigen value is also known as characteristic root or proper value. Sometimes it is also known as latent root. (2) If where S1 = a11 + a22 = sum of the diagonal elements of A. S2 = a11 . a22 - a21 . a12 = | A | (3) If Expanding this determinant we will get where S1 = sum of the diagonal elements of A S2 = sum of the minors of elements of the main diagonal S3 = |A| We will use this formula in problems. Definition 1.2.3 The set of all distinct eigen values of the square matrix A is called the spectrum of A. The largest of the absolute values of the eigen values of A is called the spectral radius of A. The set of all eigen vectors corresponding to an eigen value λ of A, together with zero vector, forms a vector space which is called the eigenspace of A corresponding to λ. Theorem 1.2.1 (1) Eigen vector corresponding to an eigen value is not unique. (2) Eigen vectors corresponding to different eigen values are linearly independent. Proof (1) Let λ be an eigen value of a square matrix A of order n. Let X be an eigen vector corresponding to λ. Then AX = λ X Multiply by a constant C ⸫ C(AX) = C(λX) ⇒ A(CX) = λ (CX) Since C ≠ 0, X ≠ 0 we have CX ≠ 0 ⸫ CX is an eigen vector corresponding to λ for any C ≠ 0. Hence eigen vector is not unique for the eigen value λ. (2) Let λ1, λ2, be two different eigen values of A. Let X1, X2 be corresponding eigen vectors. ⸫ X1 and X2 are linearly independent. Note (1) If all the n eigen values λ1, λ2,…, λn of A are different, then the corresponding eigen vectors X1, X2, ..., Xn are linearly independent. (2) A given eigen vector of A corresponds to only one eigen value of A. (3) Eigen vectors corresponding to equal eigen values may be linearly independent or dependent. Example 3 Find the eigen values and eigen vectors of the matrix Solution Let A = which are the eigen values of A. To find eigen vectors: Let Case (i) If λ = 1, then equations (I) become 3x1 + x2 = 0 3x1 + x2 = 0 ⸫ x2 = -3x1 Choosing x1 = 1, we get x2 = -3 ⸫ eigen vector is Case (ii) If λ = 5, then equations (I) become - x1 + x2 = 0 and 3x1 - 3x2 = 0 ⸫ x1 = x2 Choosing x1 = 1, we get x2 = 1 ⸫ eigen vector is Thus eigen values of A are 1, 5 and the corresponding eigen vectors are Note In case (i) we have only one equation 3x1 + x2 = 0 to solve for x1 and x2. So, we have infinite number of solutions x1 = k, x2 = -3k, for any k ≠ 0. We have chosen the simplest solution. In fact Example 4 Show that the real matrix Solution which are the eigen values of A. To find eigen vectors Let Example 5 Find the eigen values and eigen vectors of the matrix Solution where S1 = sum of main diagonal elements of A = 3 + (-2) + 3 = 4 S2 = sum of minors of diagonal elements of A = -6 + 4 + 9 – 4 + (-6) + 4 = -2 + 5 + (-2) =1 −2 + 5 + (−2) = 1 S3 = |A| = 3(−6 + 4) + 4 (3 - 4) + 4 (-1+ 2) = - 6 – 4 + 4 = -6 ⸫ The characteristic equation is λ3 - 4 λ2 + λ + 6 = 0 We choose integer factors of constant term 6 for trial solution. We find λ = -1 is a root. To find the other roots we perform synthetic division Other roots are given by To find eigen vectors: Let By rule of cross multiplication Choosing x1 = 1, x2 = 1, x3 = 0, we get an eigen vector Case (ii) If λ = 2, then equations (I) become x1 - 4x2 + 4x3 = 0 x1 - 4x2 + 4x3 = 0 x1 - x2 + x3 = 0 ⸫ the different equations are x1 - 4x2 + 4x3 = 0 x1 - x2 + x3 = 0 By the rule of cross multiplication, we get Choosing x1 = 0, x2 = 1, x3 = 1, we get an eigen vector Case (iii) If λ = 3, then equations (I) become x1 - 4x2 + 4x3 = 0 ⇒ 0x1 - x2 + x3 = 0 x1 - 5x2 + 4x3 = 0 x1 - x2 + 0x3 = 0 The equations are different, but only two of them are independent. So, we can choose any two of them to solve. From the first two equations, we get Note (1) We are using the following integer root theorem for trial solution. "For the equation of the form xn + an-1 xn-1 + an-2 xn-2 + ··· + a1x + a0 = 0 with integer coefficients ai, any rational root is an integer and is a factor of the constant term a0". So, it is enough we try factors of the constant term for integer solutions. (2) In the above problem the eigen values -1, 2, 3 are different. So by property (2) the eigen vectors are linearly independent. We shall verify this: Consider Then |B| =1.0-1(-1)+0=1≠0 ⸫ X1, X2, X3 are linearly independent. Example 6 Find the eigen values and eigen vectors of Solution where S1 = sum of the diagonal elements A = 2 + 3 + 2 = 7 S2 = sum of minors of the diagonal elements of determinant A = 6 - 2 + 4 - 1 + 6 - 2 = 4 + 3 + 4 = 11 S3 = |A| = 2(6 - 2) − 2(2 - 1) +1(2 - 3) = 8 - 2 - 1 = 5 ⸫ The characteristic equation is λ3 - 7 λ2 + 11 λ - 5 = 0 Choose the integer factors of constant term -5 for trial. The integer factors of -5 are -5, 1, or -1,5. We find λ = 1 is a root. Other roots are given by ⸫ the eigen values are λ = 1, 1, 5 (Two equal eigen values) To find eigen vectors: Let Case (i) If λ = 5, then the equations (I) become - 3x1 + 2 x2 + x3 = 0 (1) x1 - 2 x2 + x3 = 0 (2) x1 + 2 x2 + 3x3 = 0 (3) These 3 equations are different, but only 2 of them are independent. So, we can choose any two of them to solve for x1, x2, x3. From (2) and (3), by rule of cross multiplication we get Case (ii) If λ = 1, then the equations (I) become x1 + 2x2 + x3 = 0 x1 + 2x2 + x3 = 0 x1 + 2x2 + x3 = 0 We have only one equation x1 + 2x2 + x3 = 0 to solve for x1, x2, x3. Assign arbitrary values for two variables and solve for the third. Choose x3 = 0, then x1 + 2x2 = 0 ⇒ x1 = −2x2 Choose x2 = 1, ⸫ x1 = -2, we get an eigen vector We shall find one more solution from x1 + 2x2 + x3 = 0 Choose x2 = 0 then x1 + x3 = 0 ⇒ x3 = -x1 Choose x1 = 1 ⸫ x3 = − 1 ⸫ another eigen vector corresponding to λ = 1 is Thus eigen values of A are 5, 1, 1 and the corresponding eigen vectors are Note Though the eigen values are not different, we could find independent eigen vectors. For, consider Then |B| = 1(-1 - 0) — 1(2 − 0) + 1(0 − 1) = -1 - 2 - 1 = -4 ≠ 0 ⸫ X1, X2, X3 are linearly independent. Example 7 Find the eigen values and eigen vectors of the matrix Solution where S1 = sum of the diagonal elements of A = 3 + (-3) + 7 = 7 S2 = sum of minors of elements of the diagonal of A = (−21 + 20) + (21−15) + (−9 + 20) = -1 + 6 + 11 = 16 S3 = |A| = 3(-21 + 20) - 10(-14 + 12) + 5(-10 + 9) = -3 + 20 - 5 - 12 ⸫ the characteristic equation is λ3 - 7 λ2 + 16λ – 12 = 0 Choose the integer factors of constant term -12 for trial. We find λ = 2 is a root. Other roots are given by ⸫ The eigen values are λ = 2, 2, 3. (Two equal eigen values) To find eigen vectors: Let Case (i) If λ = 3, then the equations (I) become 0x1, + 10x2 + 5x3 = 0 ⇒ 0x1 + 2x2 + x3 = 0 (1) -2x1 - 6x2 - 4x3 = 0 ⇒ x1 + 3x2 + 2x3 = 0 (2) 3x1 + 5 x2 + 4x3 = 0 (3) These 3 equations are different, but only 2 of them are independent. From (1) and (2), by rule of cross multiplication we get Choosing x1 = 1, x2 = 1, x3 = −2, we get an eigen vector Case (ii) If λ = 2, then equations (I) become x1 + 10x2 + 5x3 = 0 (1) -2x1 - 5x2 -4x3 = 0 (2) 3x1 + 5x2 + 5x3 = 0 (3) From (1) and (2), by rule of cross multiplication we get In this case we cannot choose another vector independent of X2. So corresponding to the equal eigen values 2, 2 the eigen vectors are equal Thus the eigen values of A are 3, 2, 2 and the corresponding eigen vectors are Note Here X1 and X2 are linearly independent vectors as they belong to different eigen values, but X1, X2, X3 are linearly dependent vectors. See note (3) below properties. (Page 1.6) Example 8 Find the eigen values and eigen vectors of the matrix Solution where S1 = sum of the diagonal elements of A = 6 + (-13) + 4 = -3 S2 = sum of minors of elements of the diagonal of A = (−52 + 60) + (24 − 35) + (-78 + 84) = 8 – 11 + 6 = 3 S3 = |A| = 6(−52 + 60) + 6(56 − 70) + 5(−84 + 91) = 48 + 6(-14) + 5(7) = 48 - 84 + 35 - 1 ⸫ the characteristic equation is λ3 + 3 λ2 + 3 λ + 1 = 0 ⇒ ( λ + 1)3 = 0 ⇒ λ = -1, -1, -1 (3 equal eigen values) To find eigen vectors: Let X = If λ = -1, then the equations (1) become 7x1 −6x2 + 5x3 = 0 14 x1 −12 x2 + 10 x3 = 0 ⇒ 7 x1 −6 x2 + 5 x3 = 0 7x1 − 6x2 + 5x3 = 0 We have only one equation 7x1 - 6x2 + 5x3 = 0 Assign arbitrary values to two variables and find the third. We shall find 3 vectors. Putting x1 = 0, we get −6x2 + 5x3 = 0 Note If then |B| = 0 - 5(0 - 42) + 6(-35 - 0) = 210 – 210 = 0 ⸫ The vectors X1, X2, X3 are linearly dependent. However, any two of them are linearly independent. Geometrically, it means that all the vectors are coplanar, but any two of them are non-collinear. In this example we have seen −1 is the only eigen value of 3 × 3 matrix and two linearly independent eigen vectors. Example 9 Find the eigen values and eigen vectors of Solution where S1 = −5 + 9 + (−7) = −3 = (−63 + 54) + (35 −18) + (−45 + 40) = −9 + 17 – 5 = 3 S3 = |A| = −5(−63 + 54) + 5(−56 + 36) — 9(−24 + 18) = 45 – 100 + 54 = -1 ⸫ the characteristic equation is λ3 + 3 λ2 + 3λ + 1 = 0 ⇒ (λ + 1)3 = 0 ⇒ λ = -1, -1, -1 If X = Note In this example, 3 × 3 matrix has one eigen value −1 and one linearly independent eigen vector. Example 10 Find the eigen values and eigen vectors of Solution ⸫ the characteristic equation is λ3 — 5 λ2 + 7 λ − 3 = 0 Since the sum of the coefficients is zero, λ = 1 is a root. The other roots are given by To find eigen vectors: Let Case (i) If λ = 1, then equations (I) become x1 + x2 + x3 = 0 x1 + x2 + x3 = 0 0x3 = 0 Thus we have x1 + x2 + x3 = 0 Put x1 = 1, x2 = 0, then x3 = −1 Since λ = 1 is a repeated eigen value, we have to find another eigen vector. Put x1 = 0, x2 = 1 ⸫ x3 = -1 So, another eigen vector is Case (ii) If λ = 3 then equations (I) become -x1 + x2 + x3 = 0 ⇒ x1 - x2 - x3 = 0 and -2x3 = 0 ⇒ x3 = 0 x1 - x2 = 0 ⇒ x1 = x2 Take x2 = 1 ⸫ x1 = 1, x2 = 1, x3 = 0 ⸫ an eigen vector is Thus the eigen values are λ = 1, 1, 3 and the eigen vectors are Example 11 Find the eigen values and eigen vectors of the matrix Solution Where S1 = sum of diagonal elements of A = 11+ (-2) + (− 6) = 3 = (12 - 20) + (−66 + 70) + (−22 + 28) = -8 + 4 + 6 = 2 -88 +32 +56 = 0 ⸫ The characteristic equation is λ3 − 3λ2 + 2λ - 0 = 0 ⇒ λ (λ2 − 3λ + 2) = 0 ⇒ λ (λ − 1)( λ − 2) = 0 ⇒ λ = 0, 1, 2. To find eigen vectors: If Take x1 = 1, x2 = 1, x3 = 1. ⸫ an eigen vector is Case (ii) If λ = 1, then (I) ⇒ 10x1 − 4x2 − 7x3 = 0 7x1 − 3x2 − 5x3 = 0 10x1 − 4x2 − 7x3 = 0 From the first two equations, by rule of cross multiplication we get Case (iii) If λ = 2, then (I) ⇒ 9x1 − 4x2 − 7x3 = 0 7x1 − 4x2 − 5x3 = 0 10x1 − 4x2 − 8x3 = 0 From the first two equation, by rule of cross multiplication we get ⸫ The eigen values are 0, 1, 2 and the eigen vectors are Example 12 Find the eigen values and eigen vectors of the matrix Solution Let The characteristic equation of A is Where s1 = sum of the diagonal elements = 6 s2 = sum of the minors of diagonal elements of A ⸫ the characteristic equation is λ3 - 6 λ2 + 11λ − 6 = 0. By trail 1 is a root. The other roots are given by λ3 - 5λ2 + 6 = 0 ⇒ (λ − 1)( λ − 3) = 0 ⇒ λ = 2, 3. ⸫ the eigen values of A are λ = 1, 2, 3. To find eigen vectors: Let X = Case (i) If λ = 1, then the equations (1) become x1 + x3 = 0, x2 = 0 and x1 + x3 = 0 ⇒ x3 = -x1 Choose x1 = 1, then x3 = −1 ⸫ x1 = 1, x2 = 0, x3 = −1 Case (ii) If λ = 2, then the equations (I) become x3 = 0, 0.x2 = 0, x1 = 0. So, x2 can take any value. Choose x2 = 1 ⸫ x1 = 0, x2 = 1, x3 = 0 ⸫ an eigen vector is X2 Case (iii) If λ = 3, then the equations (I) become -x1 + x3 = 0, -x2 = 0, x1 - x3 = 0 x3 = 1, x2 = 0 Choose x3 = 1, then x = 1 ⸫ an eigen vector is ⸫ the eigen values of A are 1, 2, 3 and the corresponding eigen vectors are Example 13 Find the eigen values and the eigen vectors of the matrix Solution: Case (i) If λ = -2, then (I) ⇒ 3x1 + x2 + 3x3 = 0 x1 + 7x2 + x3 = 0 3x1 + x2 + 3x3 = 0 From the first two equations, by rule of cross multiplication, we get Case (ii) If λ = 3 then (I) ⇒ 2x1 + x2 + 3x3 = 0 x1 + 2x2 + x3 = 0 3x1 + x2 - 2x3 = 0 From first two equations, by rule of cross multiplication, we get Case (iii) If λ = 6 then (1) ⇒ 5x1 + x2 + 3x3 = 0 x1 - x2 + x3 = 0 3x1 + x2 - 5x3 = 0 From the first two equations, by rule of cross multiplication, we get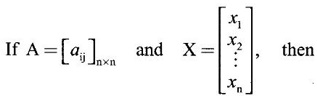
 This will represent a system of linear homogeneous equations in x1, x2, ..., xn. Since X ≠ 0 at least one of the xi ≠ 0. Hence the homogeneous system has nontrivial solutions.
This will represent a system of linear homogeneous equations in x1, x2, ..., xn. Since X ≠ 0 at least one of the xi ≠ 0. Hence the homogeneous system has nontrivial solutions. then the characteristic equation of A is
then the characteristic equation of A is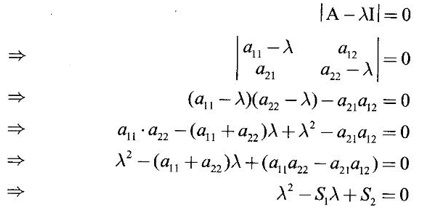
 then the characteristic equation of A is
then the characteristic equation of A is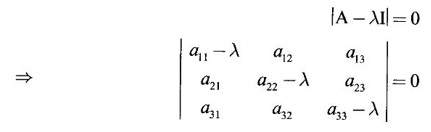
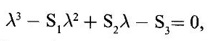
Properties of eigen vectors

WORKED EXAMPLES

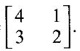 The characteristic equation of A is
The characteristic equation of A is
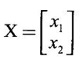 be an eigen vector of A corresponding to λ.
be an eigen vector of A corresponding to λ.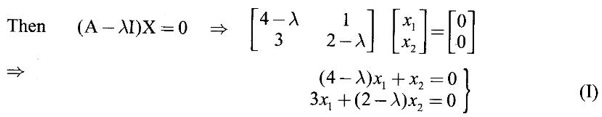
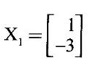

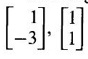
 is an eigen vector for λ = 1 for any k ≠ 0. So, for λ = 1 there are many eigen vectors. This verifies property 1.
is an eigen vector for λ = 1 for any k ≠ 0. So, for λ = 1 there are many eigen vectors. This verifies property 1. has two eigen vectors
has two eigen vectors 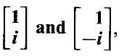 where b ≠ 0.
where b ≠ 0.
 be an eigen vector of A corresponding to λ.
be an eigen vector of A corresponding to λ.
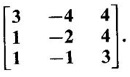
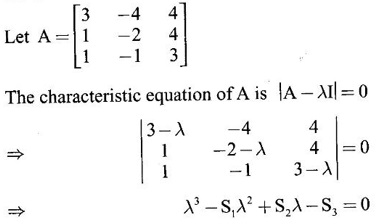

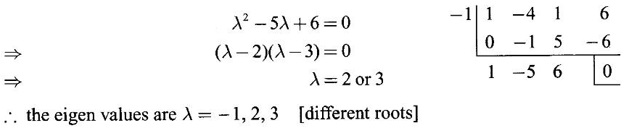
 be an eigen vector corresponding to the eigen value λ.
be an eigen vector corresponding to the eigen value λ.
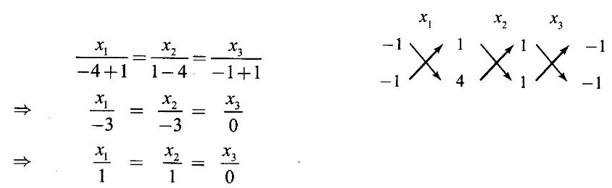

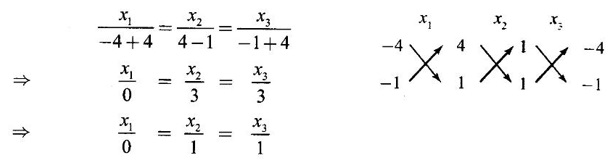


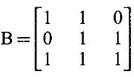 with the eigen vectors as rows.
with the eigen vectors as rows.

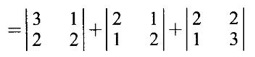

 be an eigen vector of A corresponding to the eigen value λ.
be an eigen vector of A corresponding to the eigen value λ.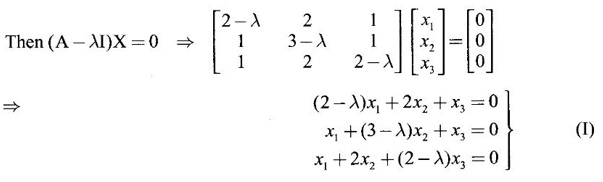

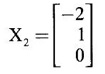
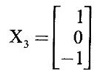
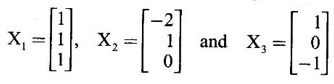
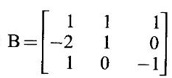 with the vectors as rows
with the vectors as rows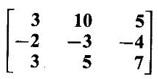


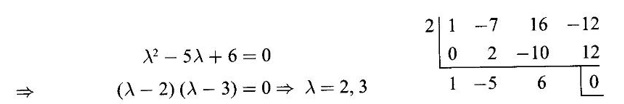
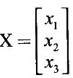 be an eigen vector corresponding to the eigen value λ.
be an eigen vector corresponding to the eigen value λ.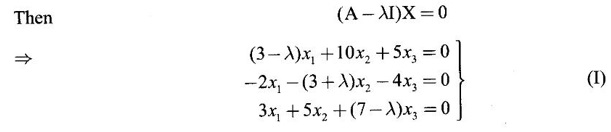
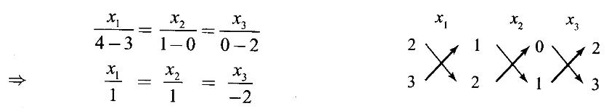


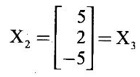
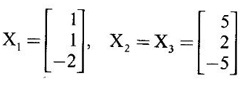

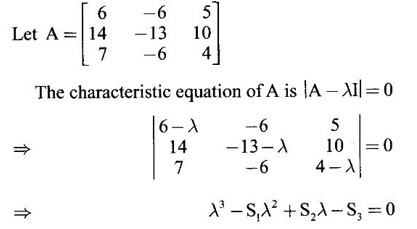
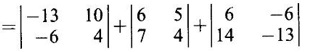
 be an eigen vector corresponding to the eigen value X.
be an eigen vector corresponding to the eigen value X.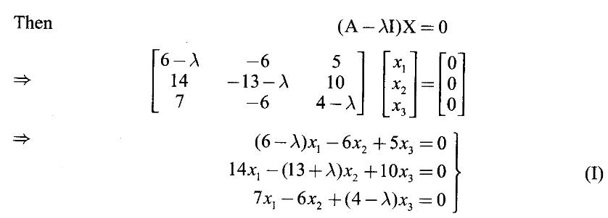

 with the eigen vectors as rows,
with the eigen vectors as rows,

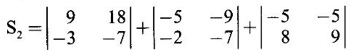
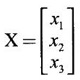 is an eigen vector of the eigen value λ,
is an eigen vector of the eigen value λ,
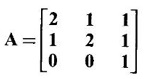


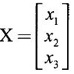 be an eigen vector corresponding to an eigen value λ of A.
be an eigen vector corresponding to an eigen value λ of A.

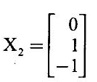
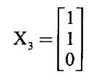


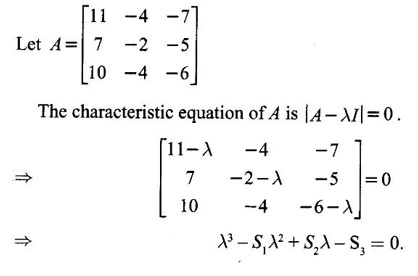

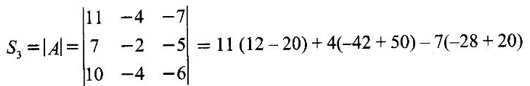
 be an eigen vector of A corresponding to λ.
be an eigen vector of A corresponding to λ.
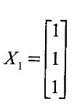




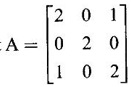
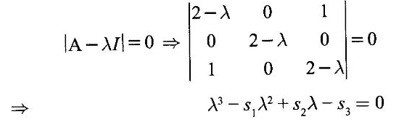
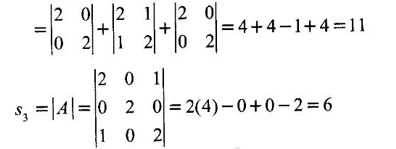
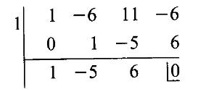
![]() be an eigen vector corresponding to eigen value λ
be an eigen vector corresponding to eigen value λ

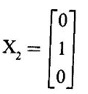
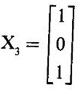
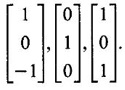


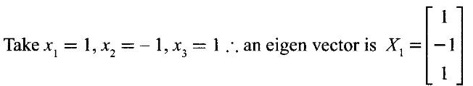

Matrices and Calculus: Unit I: Matrices : Tag: : Definition, Properties, Worked Examples - Eigen Values and Eigen Vectors
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
