Theory of Machines: Unit III: Friction in Machine Elements
Efficiency of inclined plane
Friction in Machine Elements - Theory of Machines
The efficiency of an inclined plane is defined as the ratio between the effort without friction (P0) and the effort with friction (P).
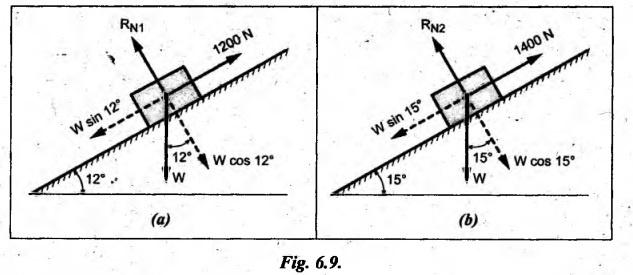
EFFICIENCY OF INCLINED PLANE • The efficiency of an inclined plane is defined as the ratio between the effort without friction (P0) and the effort with friction (P). • Mathematically, Dividing equation (6.6) by equation (6.8), we get Multiplying the numerator and denominator by sin (α + ϕ) sin θ, we get Note 1. When effort is applied horizontally, then θ = 90°. 2. When effort is applied parallel to the plane, then θ = 90° + α. Since the value of P will be less than P0, dividing equation (6.10) by equation (6.9), we get Multiplying the numerator and denominator by sin (α – ϕ) sin θ, we get Note 1. When effort is applied horizontally, then θ = 90°. 2. When effort is applied parallel to the plane, then θ = 90° + α. Example 6.2 An effort of 1200 N is required just to move a inclined plane of angle 12, the force acting parallel to the plane. If the angle of inclination of the plane is increased to 15°, then the effort required is 1400 N. Find the weight of the body and coefficient of friction. Given data: P1 = 1200 N; α1 = 12°; P2 = 1400; α2 = 15°. Solution: In both the cases, the effort is applied parallel to the inclined plane and body is just to move up. Hence the force of friction F = μ R will be acting downwards. Coefficient of friction (μ): Case (i): The body is in equilibrium under the action of forces, as shown in Fig.6.9(a). P1 = 1200 N; ά1 = 12° (given) Let F1 and RNI be the force of friction and normal reaction respectively. Resolving the forces along the plane, we get W sin 12° = F1 = 1200 or W sin 12° + μ RNI = 1200 [ ⸪ F1 = μ RN1] ... (i) Resolving the forces normal to the plane, we get RNI = W cos 12° Substituting the value of RN1 in equation (i), we get Case (ii): The body is in equilibrium under the action of forces, as shown in Fig.6.9(b). P2 = 1400 N and α2 = 15° (given) Let F2 and RN2 be the force of friction and normal reaction respectively. Resolving forces along the plane [refer Fig.6.9(b)], we get Resolving forces normal to the plane, we get RN2 = W cos 15° Substituting the value of RN2 in equation (iii), we get Weight of the body (W): The weight of the body is obtained by substituting the value of u in equation (ii) (or in (iv)).
1. Efficiency for the Motion Up the Plane


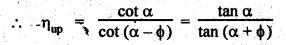

2. Efficiency for the Motion Down the Plane
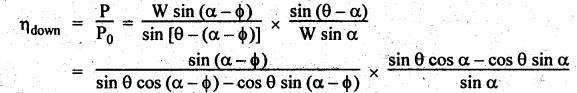


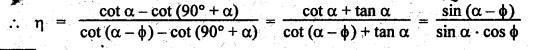




Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - Efficiency of inclined plane
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
