Theory of Machines: Unit IV: Force Analysis
dynamically equivalent systems (equimomental system)
Force Analysis - Theory of Machines
In dynamics problems, it is convenient to replace a rigid body by two separate concentrated masses placed at a fixed distance apart.
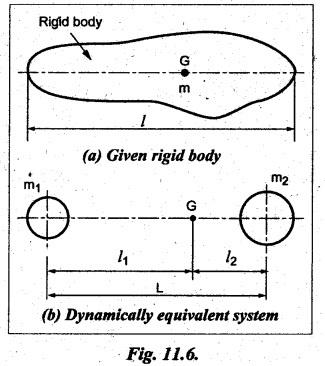
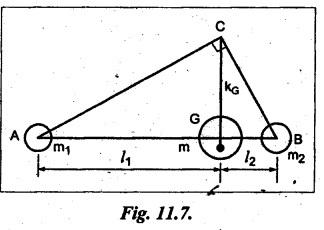
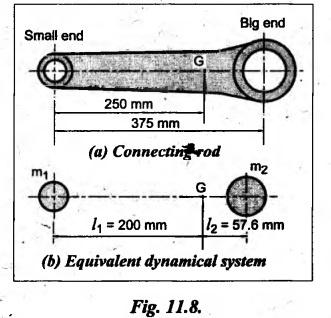
DYNAMICALLY EQUIVALENT SYSTEMS (EQUIMOMENTAL SYSTEM) • In dynamics problems, it is convenient to replace a rigid body by two separate concentrated masses placed at a fixed distance apart. • So far, we have not considered the weight of connecting rod in our force analysis. But in practice, we have to take into account the weight of the connecting rod and the inertia of the connecting rod. As the motion of the connecting rod is not linear, its inertia cannot be found as such. In such cases, we have to use the concept of dynamically equivalent system, in which the mass of the connecting rod is replaced by two separate concentrated masses placed at a fixed distance apart. 1. The mass of the rigid body must be equal to the sum of masses of two concentrated masses. 2. The center of gravity of the two masses must coincide with the center of gravity of the rigid body. 3. The sum of mass moment of inertia of two masses about their center of gravity is equal to the mass moment of inertia of the rigid body. Note In the above three conditions, if only first two conditions are satisfied, then the system is said to be statistically equivalent system. If all three conditions are satisfied, then system is called the dynamically equivalent system. 2. Determination of Two Masses of Dynamically Equivalent System Let us consider a rigid body as shown in Fig.11.6(a). Let m = Mass of the body, k = Radius of gyration about its center of gravity G, m1 and m2 = Two masses which form a dynamical equivalent system, l1 = Distance of mass m1 from G, l2 = Distance of mass m2 from G, and L = Total distance between the masses m1 and m2 The two masses m1 and m2 can be determined by both analytically and graphically. 1. Analytical Method Applying the three conditions of equivalent dynamical system, we get Substituting the values of m1 and m2 in equation (iii), we get If radius of gyration k of the rigid body is known, by choosing l1 arbitrarily, l2 can be determined from the above equation. Note • When the radius of gyration k is not known, then the position of the second mass may be obtained by considering the body as a compound pendulum. • We know that for a simple pendulum to have the same frequency of oscillation as that of a Compound pendulum, the equivalent length of a simple pendulum is given by where h = Distance of C.G from the point of suspension. From equation (11.23), l1l2 = k2. This means that if the first mass m1 is considered to be situated at center of suspension A (at a distance l1 from G), then the second mass m2 is situated at the center of oscillation or percussion of the body, which is at a distance of l2 = k2/ l1. • It may be useful to recollect the expressions for time period and frequency of simple and compound pendulums. 1. Simple pendulum: 2. Compound pendulum: where k = Radius of gyration about an axis passing through its centre of gravity, and h = Distance of point of suspension from the C.G 2. Graphical Method Consider a rigid body of mass m, which acts at G, and radius of gyration k, as shown in Fig.11.7. The mass m can be replaced by two masses m1 and m2 so that the system becomes dynamically equivalent. The position of mass m1 is arbitrarily fixed at A. The position of mass m2 is determined graphically as below: Draw perpendicular CG at G equal to k. Then join AC and draw a line perpendicular to AC intersecting AG produced at B, as shown in Fig.11.7. The point B gives the position of mass m2. From similar triangles ACG and BCG, we can write, (which is the same expression as in analytical method) Example 11.16 A connecting rod of length 375 mm between centers has a mass of 4 kg. The center of gravity is 250 mm from the small end and the radius of gyration about an axis through the centre of gravity perpendicular to the plane of motion is 120 mm. Determine dynamically equivalent system having one mass at the centre of small end and the other at a point somewhere in between the centre of big end and the centre of gravity. Given data: l = 375 mm = 0.375 m; l1 = 250 mm = 0.25 m; m = 4 kg; k = 120 mm = 0.12 m. Solution: Fig.11.8(a) shows the given connecting rod whereas Fig.11.8(b) shows the equivalent dynamical system. Let m1 = Mass at small end centre, and m2 = Mass at the centre of big end and centre of gravity. We know that for dynamically equivalent system, Example 11.17 The length of a connecting rod of an engine is 500 mm measured between the centers and its mass is 18 kg. The centre of gravity is 125 mm from the crank pin centre and the crank radius is 100 mm. Determine the dynamically equivalent system keeping one mass at the small end. The frequency of oscillation of the rod, when suspended from the centre of small end is 43 vibrations per minute. Given data: l = 500 mm = 0.5 m; m = 18 kg; l2 = 125 mm = 0.125 m; r = 100 mm = 0.1 m. Solution: We know that Frequency of oscillation = Number of vibrations per second The connecting rod is shown in Fig.11.9(a). Now let us find the radius of gyration k of the connecting rod, considering it as a compound pendulum, about an axis passing through its centre of gravity, G. We know that for a compound pendulum, time period of oscillation (tP), On solving, we get k = 0.202 m It is given that one of the masses is located at the small end centre. Let the other is located at a distance l2 from the centre of gravity G, as shown in Fig.11.9(b). For a dynamically equivalent system, we can write • For our solution, this data is superfluous. Then the masses at the small end centre (m1) and at the big end centre (m2) are given by1. Conditions of Equivalent Dynamical System
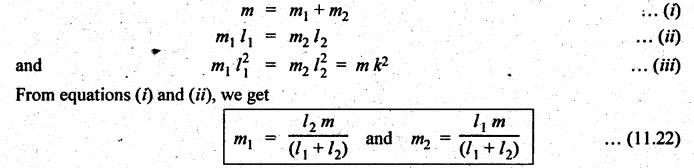
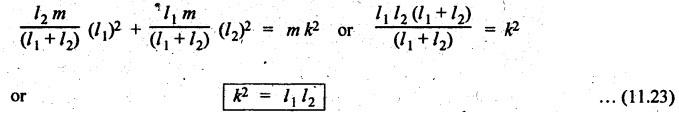
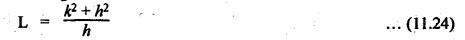
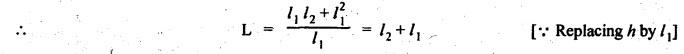
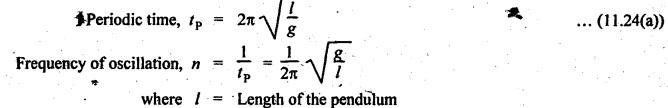

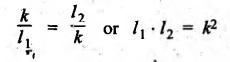
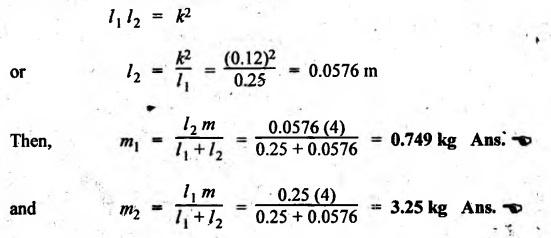

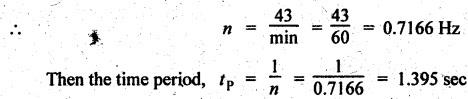
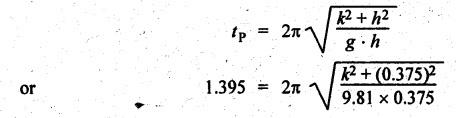
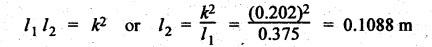

Theory of Machines: Unit IV: Force Analysis : Tag: : Force Analysis - Theory of Machines - dynamically equivalent systems (equimomental system)
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
