Theory of Machines: Unit IV: Force Analysis
Dynamic Force Analysis
Force Analysis - Theory of Machines
As already stated, when the inertia effect due to the rotating/reciprocating parts is considered in addition to the externally applied loads, such a force analysis is known as dynamic force analysis.
Chapter: 11 Dynamic Force Analysis While reading and after studying this chapter, you will be able to: • State and explain D'Alembert's principle. • Determine the velocity and acceleration of various parts of a reciprocating engine using analytical method. • Deduce an expression for the inertia force in reciprocating parts, neglecting the weight of the connecting rod. • Understand the concept of dynamically equivalent system. • Determine the inertia torque on the crank-shaft in the reciprocating parts analytically, considering the weight of the connecting rod. SYLLABUS Dynamic force analysis - Inertia forces and inertia torque D'Alembert's principle - Dynamic- force analysis in reciprocating mechanisms - Analytical and graphical methods. • As already stated, when the inertia effect due to the rotating/reciprocating parts is considered in addition to the externally applied loads, such a force analysis is known as dynamic force analysis. • Dynamic forces are associated with accelerating masses. We know that almost all machines have some accelerating parts; therefore the dynamic forces are always present when the machine operates. • Dynamic force analysis are very important in situations where dynamic forces are dominant and operating speeds are high. For example, in case of IC engines, which rotate at very high speed, even the slightest eccentricity at the centre of mass from the axis of rotation causes very high magnitude of dynamic forces. This may lead to vibrations, wear, noise or even machine failure. • In the following sections, we shall discuss the inertia forces and their effects in IC engines. 1. Inertia • We know that according to Newton's first law of motion a body continues in its state of rest or of uniform motion in a straight line, except in so far as it is compelled to change that by external force. This means that bodies offer resistance to any change of their state. of matter offering resistance to any change of its state of rest or • Definition: The property of matter offering resistance to any change of its state of rest or of uniform motion in a straight line is known as inertia. 2. Inertia Force • We know that according to Newton's second law of motion, the rate of change of momentum of a body acted upon by a force or forces is proportional to the magnitudes of the resultant external force and acts in the direction of force. • Mathematically, where m = Mass of the body, ν = Velocity of the body, a = Acceleration of the body, and F = External (or accelerating) force. • The inertia of the body opposes this external force applied (F) and it is known as inertia force. • In other terms the inertia force is a fictitious (i.e., an imaginary) force which when acts upon a rigid body, brings it in an equilibrium. It is numerically equal to the accelerating force in magnitude but opposite in direction. 3. Inertia Torque • We know that what holds good for linear motion also holds good for angular motion. Thus the inertia torque is equal and opposite to the torque applied. • We know that according to Newton's second law of motion, when applied to rotating bodies, states that "the torque is directly proportional to the rate of change of angular momentum”. • Mathematically, Since I is constant, therefore where I = Mass moment of inertia of the body, ω = Angular velocity of the body, α = Angular acceleration of the body, and T = External (or accelerating) torque. • The inertia of the body opposes this external torque applied (T) and it is known as inertia torque. • In other terms, the inertia torque is an imaginary torque, which when applied upon the rigid body, brings it in equilibrium position. It is equal to the accelerating torque (or couple) in magnitude but opposite in direction. • D'Alembert's principles states that, the inertia forces and torques, and the external forces and torques, acting on a body together result in statical equilibrium. • The equations (11.1) and (11.2) can also be written as The above equations are known as D'Alembert's principle. It can be noted that the equations (i) and (ii) can also be written as • D'Alembert's principle is summarized as follows: "The vector sum of all external forces and inertia forces acting upon a system of rigid bodies is zero. The vector sum of all external moments and inertia torques acting upon a system of rigid bodies is also separately zero.” • Application of D'Alembert's principle: This principle is used to reduce a dynamic analysis problem into an equivalent problem of static equilibrium.Learning Objectives
INTRODUCTION
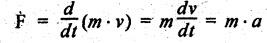
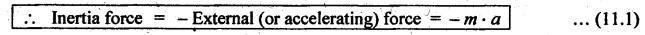
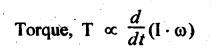
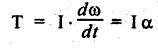

4. D'Alembert's Principle


Theory of Machines: Unit IV: Force Analysis : Tag: : Force Analysis - Theory of Machines - Dynamic Force Analysis
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
