Engineering Physics: Unit I: Mechanics
Double Pendulum
Definition, Equation, Kinematics, Forces, Uses
A double pendulum is a pendulum with another pendulum attached to its end.
DOUBLE PENDULUM A double pendulum is a pendulum with another pendulum attached to its end. It is a simple physical system that exhibits rich dynamic behaviour with strong sensitivity to initial conditions. The pendulum behaves like a linear system for small angles. When the angles, are small in the double pendulum, the system behaves like the linear double spring. In this case, the motion is determined by simple sine and cosine functions. On the otherhand for large angles, the pendulum is non-linear and the phase graph becomes much more complex. The pendulum rods are treated as massless and rigid. The derivation of the equations of motion is shown below, using the direct Newtonian method. Kinematics deals with the motion of object without regard to forces. In kinematics expressions for the position, velocity, and acceleration are given in terms of the variables that specify the state of the device. (Fig. 1.46) • x = horizontal position of pendulum mass • y = vertical position of pendulum mass • θ = angle of pendulum (O = vertical downwards, counter-clockwise is positive) • L = length of rod (constant) The origin is taken at the pivot point of the upper pendulum. The positions of pendulum 1 and pendulum 2 are found by using simple trigonometry relation. Let position of pendulum 1 be (x1 y1) and pendulum 2 (x2 y2). x1 y1 and x2 y2 are given interms of θ1 and θ2 respectively. x1 = L1 sin θ1 y1 = - L1 cos θ1 x2 = x1 = L2 sin θ2 y2 = - y1 – L2 cos θ2 The velocity is the derivative with respect to time of the position. The acceleration is the second derivative. The two pendulum masses are treated as point particles. The free body diagram is drawn for the upper mass and writing an expression for the net force acting on it (Fig. 1.47). These variables are defined as follows. • T = tension in the rod • m = mass of pendulum • g = acceleration due to gravity The forces on the upper pendulum mass are the tension in the upper rod T1 the tension in the lower rod T2, and gravity - m1g We write separaie equations for the horizontal and vertical forces, since they can be treated independently. The net force on the mass is the sum of these. Here we show the net force and use Netwon's law F = ma. For the lower pendulum, the forces are the tension in the lower rod T2, and gravity – m2g. In relating these equations to the diagrams, keep in mind that in the example diagram θ1 is positive and θ2 is negative, because of the convention that a counter-clockwise angle is positive. The double pendulum is widely used in education, research and applications. For example the double pendulum is staple bench top experiment for introducing and studying chaos and state transitions. It has also been used to study chaos both experimentally and numerically.Kinematics of the double pendulum
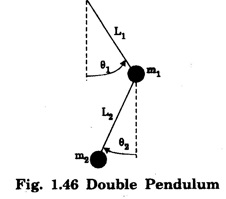
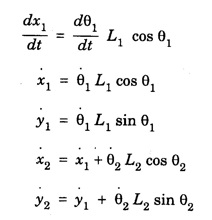
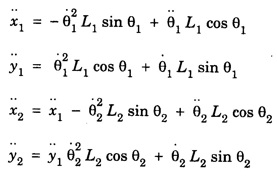
Forces in double pendulum
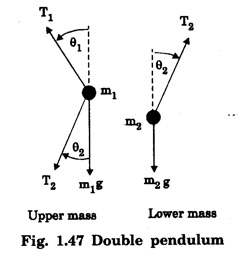
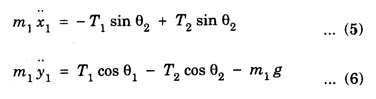
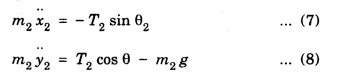
Uses of double pendulum
Engineering Physics: Unit I: Mechanics : Tag: : Definition, Equation, Kinematics, Forces, Uses - Double Pendulum
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
