Matrices and Calculus: Unit II: Differential Calculus
Differentiation of Parametric Equations
Definition, Worked Examples, Exercise with Answers | Differential Calculus
We have seen differentiation of a function given in explicit form y = f(x) and in implicit form F(x, y) = 0.
DIFFERENTIATION OF PARAMETRIC EQUATIONS We have seen differentiation of a function given in explicit form y = f(x) and in implicit form F(x, y) = 0. In applications, sometimes it will be convenient to parametrize the equations of curves. That is to write the current coordinates x and y as functions of a variable t, called the parameter. For example x2 + y2 = 1 can be written as x = cos θ, y sin θ, where θ is the parameter. Let x = f(t) and y = g(t) be the parametric equations, where ƒ and g are differentiable and f is invertible i.e. f has inverse F, say We shall rewrite in Leibntz notation This process of obtaining derivatives is called parametric differentiation. Example 1 Solution Given the parametric equations Example 2 Solution Gives the parametric equations Example 3 Solution Given the parametric equations Example 4 Solution Given the parametric equations Example 5 If x = 3 sin t - sin3 t, y = 3 cos t - cos3 t, then find dy/dx Solution Given the parametric equations Differentiate the following functions (implicitly and parametrically) and find dy/dx
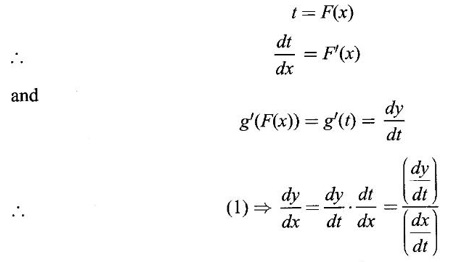
WORKED EXAMPLES

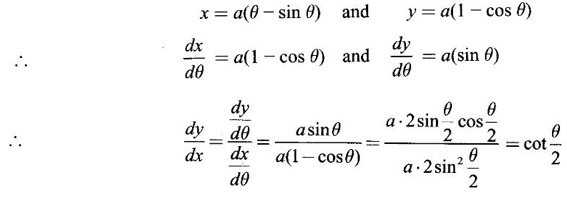
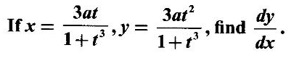





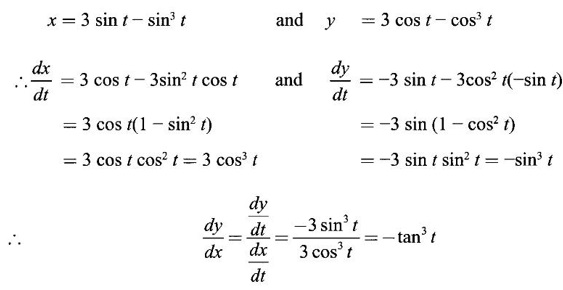
EXERCISE 2.8
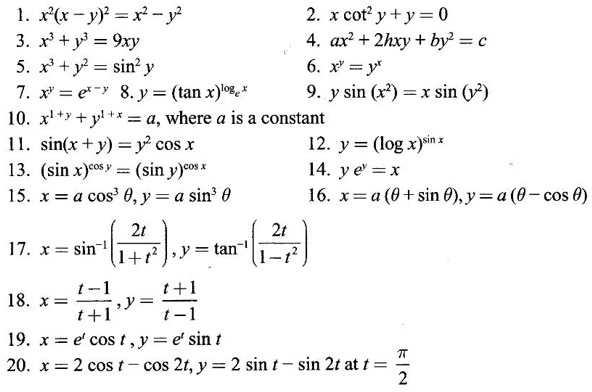
ANSWERS TO EXERCISE 2.8

Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Worked Examples, Exercise with Answers | Differential Calculus - Differentiation of Parametric Equations
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
