Matrices and Calculus: Unit II: Differential Calculus
Derivative of Inverse Functions
Trigonometric Functions, Worked Examples, Exercise with Answers | Differential Calculus
Worked Examples, Exercise with Answers: Derivative of Inverse Functions: Matrices and Calculus: Differential Calculus
DERIVATIVE OF INVERSE FUNCTIONS Let ƒ be a differentiable function and one-one with domain Df. For a∈Df let f'(a) exist and ƒ'(a) ≠ 0. Let g be the inverse of f, then g is differentiable and g'(f(a)) = 1/f'(a) In Leibnitz notation Let y = f(x), then x = g(y) then In other words, Example 1 Differentiate the following with respect to x Solution Example 2 Differentiate the following with respect to x Solution Example 3 Differentiate the following with respect to x Solution Example 4 Find dy/dx from the following Solution Example 5 Find the derviative of Solution Example 6 Find the derivative of f(x) = Solution Differentiate the following functions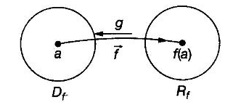
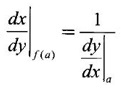
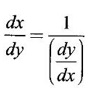at the corresponding points.1. Derivative of Inverse Trigonometric Functions
WORKED EXAMPLES
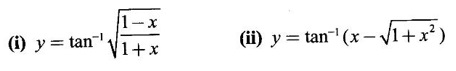
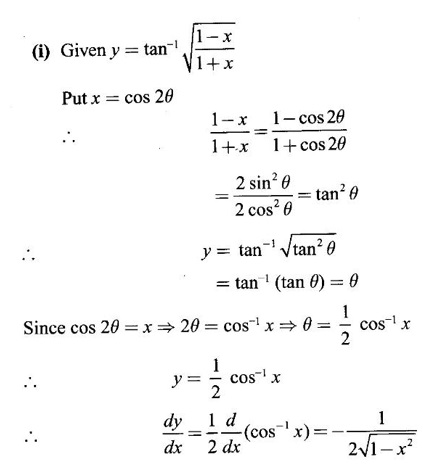
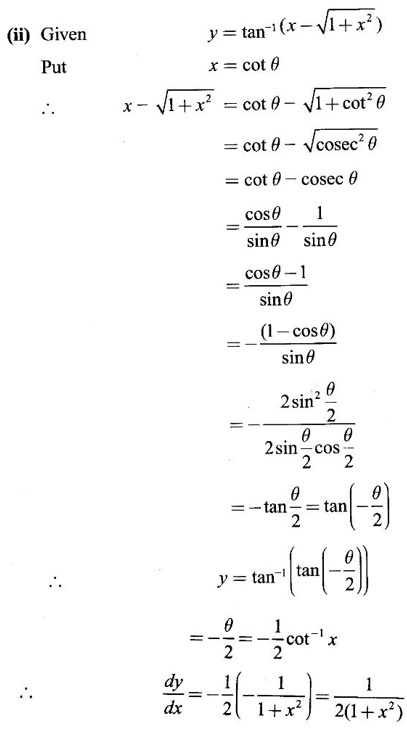
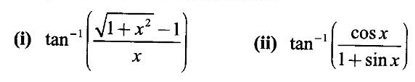
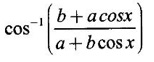
EXERCISE 2.7
ANSWERS TO EXERCISE 2.7.
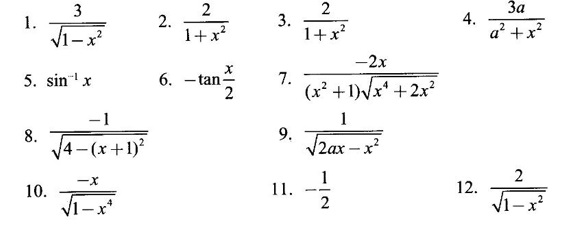
Matrices and Calculus: Unit II: Differential Calculus : Tag: : Trigonometric Functions, Worked Examples, Exercise with Answers | Differential Calculus - Derivative of Inverse Functions
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation