Matrices and Calculus: Unit II: Differential Calculus
Derivative
Definition, Theorem, Solved Example Problems | Differential Calculus
Intuitively, a function is derivable or differentiable at a point c if the graph of the function in a neighbourhood of c is a smooth curve without sudden changes in the direction of the graph.
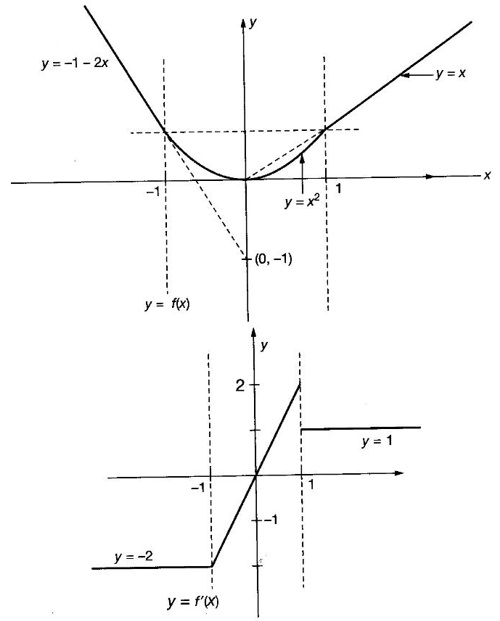
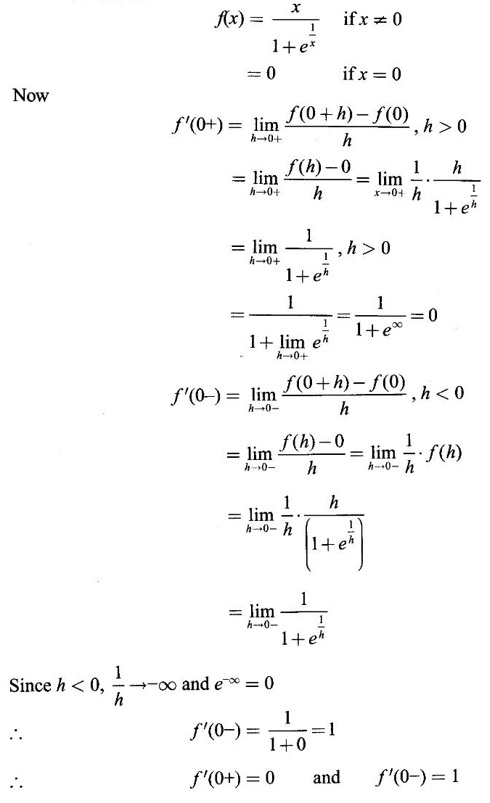
DERIVATIVE Intuitively, a function is derivable or differentiable at a point c if the graph of the function in a neighbourhood of c is a smooth curve without sudden changes in the direction of the graph. The central idea of differential calculus is the notion of derivative. The concept of derivative originated with the tangent at a point on curve. The solution to this problem also provided a way to calculate velocity and more generally the rate of change of a function. Calculus thus became the mathematics of change. Definition 2.17 Derivative Let f be a function defined in a neighbourhood (c - δ, c + δ) of a point c, where δ > 0 and small. f is said to be derivable or differentiable at c if Then it is denoted by f'(c) and is called the derivative of f at c. Since derivative is defined as a limit we may have derivative on one-side only the left derivative or the right derivative. Right derivative at c is defined as f'(c +) = Theorem 2.8 f'(c) exists if and only if f'(c-) and ƒ'(c+) exist and are equal. Then f'(c)= f'(c−) = f'(c+) Theorem 2.9 Differentiability ⇒ continuity If f is differentiable at c, then f is continuous at c. Proof: Given f is differentiable at c Hence, f is continuous at c But the converse is not true. i.e., f is continuous at c does not imply ƒ is differentiable at c. We shall show this in the next example 1. We have seen f'(c) as the derivative of f at the point c. Suppose for a given function f, if the derivative ƒ'(x) exists for infinitely many points, x in its domain, then we can regard ƒ' as a function derived from f by the limiting process If f'(x) exists at every point x in the domain of f, then we say ƒ is differentiable. Obtaining f'(x) at an arbitrary point x is referred to as differentiation with respect to x. The notation f' was introduced by Lagrange in late 18th century. Leibnitz used y for f(x) Δy for f(x + h) - f(x) Δx for (x + h) - x = h Definition 2.18 A function ƒ defined in an open interval (a, b) is said to be differentiable in (a, b) if ƒ'(x) exists ∀x∈(a, b). A function ƒ defined on a closed interval [a, b] is said to be differentiable on [a, b] if (i) f'(x) exists ∀x∈(a, b) (ii) ƒ'(a+) exists and (iii) ƒ'(b−) exists. We shall first apply the definition in some simple functions. Example 1 Test the function |x| differentiable at x = 0. Solution Hence f'(0) does not exist i.e., f is not differentiable at x = 0 We have seen in Example 12, section 2.4, |x| is continuous at x = 0 [and in fact |x| is continuous ∀x∈ (-∞, ∞)]. So continuity does not imply differentiability. * But not continuous ⇒ not differentiable Example 2 Find the derivative of the function f(x) = x2 − 8x + 9 at the point 2. Solution Given f(x) = x2 − 8x + 9 Required f'(2) Example 3 If f(x) = x3 − x, find a formula for ƒ'(x) Solution Given f(x) = x3 − x Example 4 Where the function f(x)= |x| is differentiable? Solution Given We have seen in example 1, f is not differentiable at x = 0 If x > 0, |x| = x For any c in (0, ∞) Since c > 0, |c| = c We can choose h very small so that c + h > 0 So, f'(c) exists and c is arbitrary in (0, ∞) ⸫ f is differentiable is (0, ∞) Now, consider the interval (-∞, 0) and let c be any point in (-∞, 0) Given a differentiable function ƒ we have seen the process of getting its derivative f'. If f' is also differentiable we can find its derivative (f')'= ƒ" and is called the second derivative of f. Proceeding this way can be find the nth derivative ƒ(n)of f, which is the first derivative of f(n−1) We shall now discuss the general techniques or rules of differentiation. Sum Rule 3. If u and v are differentiable functions of x then u + v and u – v are differentiable. 4. Product Rule If u and v are differentiable functions of x, then uv is differentiable and Proof: Let f(x) = u(x) v(x) 5. Quotient Rule If u and v are differentiable functions of x and if v(x) ≠ 0, then We shall now find derivatives of some standard functions. 1. Proof: Let f(x) = xn 2. Proof: Let f(x) = ax Then 3. Proof: Let f(x) = loge x 4. Proof: Let f(x) = sin x 5. Proof: Let f(x) = cos x 6. Proof: Let f(x) = tan x Similarly, we can prove * Any polynomial function is differentiable everywhere. Example 5 Solution Given f(x) = To test f is differentiable at 1, we find the left and right derivatives at 1. f(1) = 2 - 1 = 1 Hence, f'(1) does not exist. So, f is not differential at x = 1 But in the open interval (-∞, 1), f(x) = 2 − x, which is differentiable ⸫ f'(x) = -1 In the open interval (1, ∞), f(x) = x2 − 2x + 2, which is a polynomial and so differentibale f'(x) = 2x − 2 Example 6 At what numbers, the following function g differentiable? Give a formula for f'. Sketch the graph of ƒ and f'. Solution Given f(x) = We test for derivative at x = -1 and x = 1 At x = -1 ⸫ ƒ'(1-) ≠ ƒ'(1+) Hence, f'(1) does not exist In the interval (-∞, −1), f(x) = -1 - 2x, which is a polynomial ⸫ f'(x) = -2 In the interval (−1, 1), f(x) = x2 ⸫ f'(x) = 2x In the interval (1, ∞), f'(x) = x f'(x) = 1 We shall draw the graph of ƒ and ƒ'. If x = 1, y = -2x - 1, which is a straight line It meets the x-axis at the point (-1/2, 0) and the y-axis at the point (0, -1) If −1 ≤ x ≤ 1, then graph of y = x2 is a parabola upward. If x > 1, then graph of y = x is a straight line. Example 7 For what values of x, is the function f(x) = |x2 − 9| differentiable? Find a formula for ƒ'. Solution We test for derivative at x = −3 and x = 3 At x = -3 f(x) is defined for all x∈ (−∞, ∞), it is differentiable for all x ∈ (-∞, ∞) except x = -3 and x = 3 Example 8 For what values of x, the function f(x) = |x −1| + |x + 2| is differentiable? Give formula for ƒ' and sketch ƒ and ƒ' Solution Given f(x) = |x −1| + |x + 2| Mark the points x = -2 and x = 1 Then we have 3 intervals (-∞, −2), (−2, 1), (1, ∞) If x < -2, then x + 2 < 0, x - 1 < 0 It can be easily seen f(x) is continuous for all x ∈ (−∞, ∞) We test for differentiability at x = 1, x = -2 At x = -2: f'(1) does not exist. f(x) is differentiable for all x∈(-∞, ∞), except x = −2 and x = 1. and We shall now draw the graph of ƒ. When x = 0, y = 1 and when y = 0, x = -1/2 Remark: Look at the graph of f, at x = -2 the graph changes from y = -2x - 1 to y = 3 and the changes is not smooth because ƒ' (−2) does not exist. At x = 1, the graph changes form y = 3 to y = 2x + 1, and the change is not smooth because ƒ' (1) does not exist. Example 9 Find ƒ'(1), if it exists. Solution Given Example 10 f(x) = Prove that f is continuous but not deliverable at x = 0. Solution Hence, f is continuous at x = 0 which does not exist ⸫ f is not differentiable at x = 0, but differentiable everywhere else Example 11 Show that f(x) = Is differentiable at x = 0 and find ƒ'(0). Solution So, f is differentiable at x = 0 and ƒ'(0) = 0 Example 12 Find the values of a and b so that f is differentiable ∀x. Solution Given Suppose ƒ is differentiable for all x, then f is differentiable at x = 2 Hence, f is continuous at x = 2 Substitute in (1), b = 4 – 2a = 4 – 8 = -4 a = 4, b = -4 Note: A useful result for computation of problems of above type. If f is continuous at c and if Example 13 For the function f(x) : Find ƒ'(0+) and ƒ'(0–). Solution Given 1. At what points fis differentiable and give a formula for ƒ'. 2. Find the points where f(x) = |4 - x2| is not differentiable. Find a formula for f'. 3. Show that f(x) = 4. Show that f(x) = 5. f(x) = find a and b if ƒ'(2) exists. [Hint: f is continuous at x = 2] 6. Does the function f(x) = 7. For what values of a and b will f(x) = 8. For what values of a and b will g(x) = 9. f(x) = 10. Show that the function f(x) = |x − 6| is not differentiable at x = 6. Find a formula for f'. Using the definition of derivative (or first principles) find the derivative of the following functions.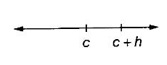
 exists.
exists.1. One-side Derivative
 if the limit exists, h > 0.
if the limit exists, h > 0.

2. Derivative as a Function
 The process of obtaining ƒ' from ƒ is called differentiation and ƒ' is called the first derivative of f. The domain of f' is the set {x | ƒ'(x) exists}.
The process of obtaining ƒ' from ƒ is called differentiation and ƒ' is called the first derivative of f. The domain of f' is the set {x | ƒ'(x) exists}.3. Leibnitz Notation

4. Differentiability in an Interval
WORKED EXAMPLES



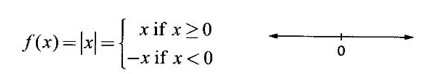

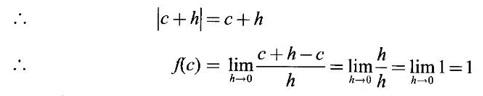

5. Higher Order Derivatives
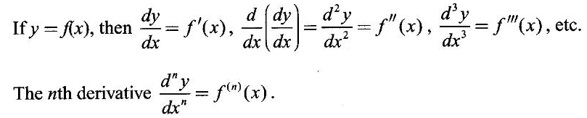


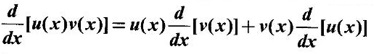


6. Power Function
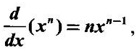 where n is a rational number.
where n is a rational number.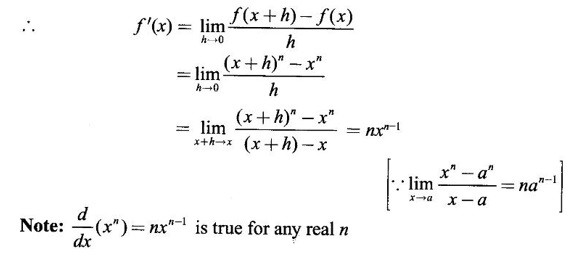
7. Exponential Function
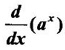 = (ax) loge a, a > 0, a ≠ 1
= (ax) loge a, a > 0, a ≠ 1 


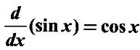

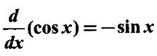
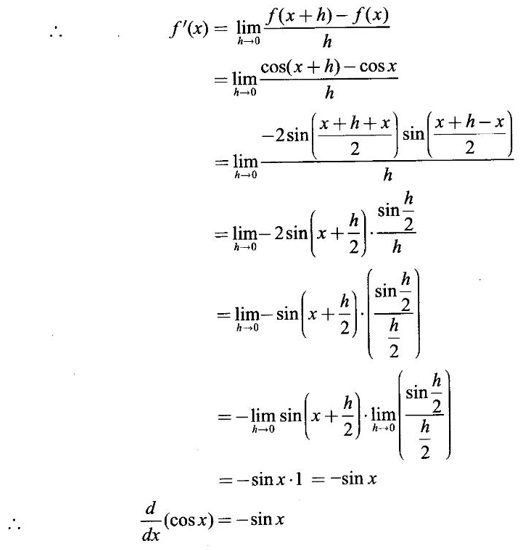


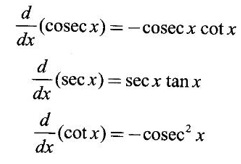
WORKED EXAMPLES
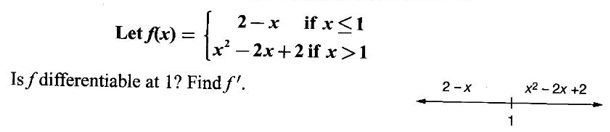
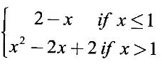

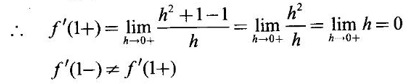

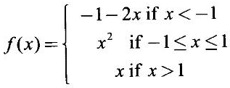


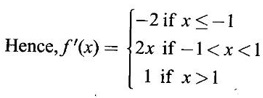
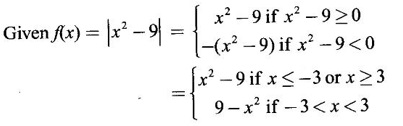


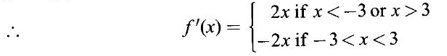


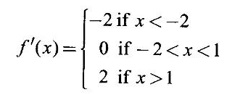


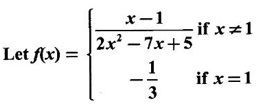

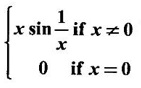

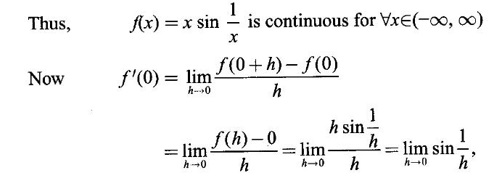

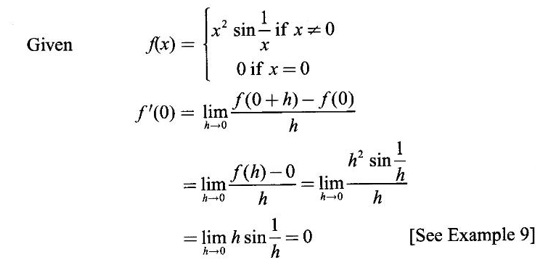
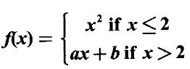

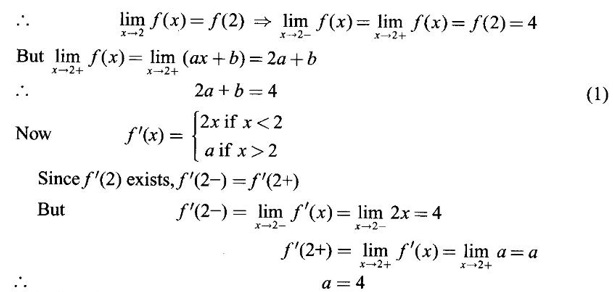
![]() f'(x) exists, then
f'(x) exists, then ![]() f'(x) = ƒ'(c).
f'(x) = ƒ'(c).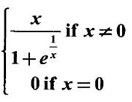
EXERCISE 2.5
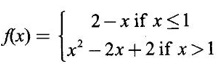
 is continuous and differentiable at x = 1
is continuous and differentiable at x = 1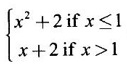 is continuous but not differentiable at x = 1
is continuous but not differentiable at x = 1
 have a derivative at x = 0? Explain.
have a derivative at x = 0? Explain. differentiable for all values of x.
differentiable for all values of x. is differentiable at x = -1
is differentiable at x = -1 Does f'(0) exist?
Does f'(0) exist?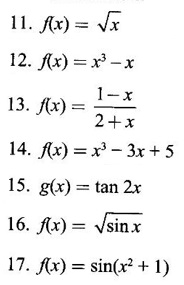
ANSWERS TO EXERCISE 2.5

Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Theorem, Solved Example Problems | Differential Calculus - Derivative
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
