Degrees of freedom (or mobility) of a mechanism

DEGREES OF FREEDOM (OR MOBILITY) OF A MECHANISM

• The mobility or number of degrees of freedom is one of the main concerns in the design or analysis of a mechanism.

• Definition: The degree of freedom is the number of independent parameters required to specify the location of every link within a mechanism.

• The mobility of a mechanism is defined as the number of inputs required to produce the constrained motion of the mechanism.

• Thus essentially both degrees of freedom and mobility are the same.

1. Planar Mechanism Vs Spatial Mechanism

1. Planar Mechanism

• A mechanism formed when all the links of the mechanism lie in the same plane is known as planar mechanism.

• Thus a planar mechanism can have maximum of three degrees of freedom.

• It may be noted that most of the mechanisms dealt in this subject are planar mechanisms.

2. Spatial Mechanism

• A mechanism formed when the links of the mechanism lie in different planes is known as spatial mechanism.

• Spatial mechanisms have special geometric characteristics. To describe the motion of such mechanisms, more than one plane would be required. For example, motions of robot arm, crane, and Hooke's joint.

• A spatial mechanism can have maximum of six degrees of freedom (three translatory motions in X, Y and Z axes, and three rotational motions about X, Y and Z axes).

2. Kutzbach Criterion for Mobility of Planar Mechanisms

• The Kutzbach criterion to find degrees of freedom of a planar mechanism in terms of number of lower and higher pairs is given by

where n = Number of links,

l - Number of lower pairs,

= j, Number of binary joints, and

h = Number of higher pairs

3. Kutzbach Criterion for Mobility of Spatial Mechanisms

Degrees of freedom of a mechanism in space can be determined with the help of following Kutzbach criterion.

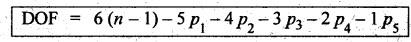
where n = Number of links in the mechanism,

p₁ = Number of pairs having 1 DOF,

p₂ = Number of pairs having 2 DOF,

p₃ = Number of pairs having 3 DOF,

p₄ = Number of pairs having 4 DOF, and

p₅ =  Number of pairs having 5 DOF

4. Grubler's Criterion for Planar Mechanisms

• Grubler's criterion is applied to mechanisms with only single degree of freedom joints where the overall mobility of the mechanism is unity.

• Substituting h = 0 and n = 1 into Kutzbach criterion for planar equation. i.e., in equation (1.4), we get

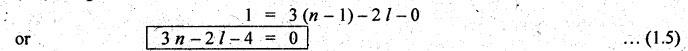
The above equation is known as Grubler's criterion for planar mechanisms with constrained motion.

5. Grubler's Criterion for Spatial Mechanisms

• If we have all single degree of freedom pairs and mobility of 1, then the Kutzbach criterion is called as Grubler's criterion for spatial mechanisms:

• Substituting n = 1, p₂ = p₂ = ……= p₅ = 0 into Kutzbach criterion for spatial equation i.e., in equation (1.5), we get

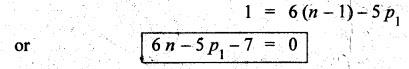
The above equation is known as Grubler's criterion for spatial mechanisms.

Example 1.3

Using Kutzbach criterion, find the degrees of freedom for the following kinematic chains: (a) Three-bar chain; (b) Four-bar chain; (c) Cam with roller follower; and (d) Cam with knife-edge follower.

Solution:

The Kutzbach criterion for planar mechanism is given by

DOF = 3 (n - 1) – 2l - h

where n = Number of links in the mechanism,

l = Number of lower pairs,

= j, Number of binary joints, and

h = Number of higher pairs

(a) For three-bar chain: Refer to Fig. 1.24(a).

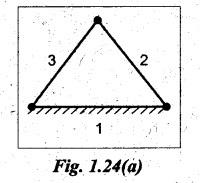
Number of links, n = 3

Number of binary joints, j = 3

⸫ Number of lower pairs l = j = 3

Number of higher pairs, h = 0

⸫ DOF = 3 (3-1)-2 (3) - 0 = 0 Ans. 

DOF = 0 means the three-bar chain forms a structure and no relative motion between the links is possible

(b) For four-bar chain: Refer to Fig. 1.24(b).

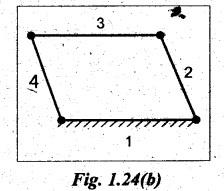
Number of links, n = 4

Number of binary joints, j = 4

⸫ Number of lower pairs l = j = 4

Number of higher pairs, h = 0

⸫ DOF = 3(4 - 1) – 2 (4) – 0 = 1 Ans. 

DOF = 1 means the four-bar chain can be driven by a single input metion,

(c) For cam with roller follower: Refer to Fig. 1.24(c).

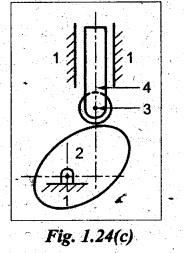
Number of links, n = 4

Number of binary joints, j = 3

⸫ Number of lower pairs l = j = 3

Number of higher pairs, h = 1

 [ ⸪ roller and cam form higher pair]

⸫ DOF = 3(4 - 1) – 2 (3) – 1 = 2 Ans. 

DOF = 2 means two separate input motions are necessary to produce constrained motion for the mechanism.

(d) For cam with knife-edge follower: Refer to Fig.1.24(d).

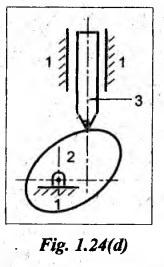
Number of links, n = 3

Number of binary joints, j = 2

⸫ Number of lower pairs l = j = 2

Number of higher pairs, h = 1

 [ ⸪ knife-edge and cam form higher pair]

⸫ DOF = 3(3 - 1) – 2 (2) – 1 = 1 Ans. 

DOF = 1 means the mechanism can be driven by a single input motion.