Strength of Materials: Unit III: Torsion
deflection of shaps fixed at both ends
Torsion - Strength of Materials
deflection of shaps fixed at both ends: Torsion - Strength of Materials
DEFLECTION OF SHAPS FIXED AT BOTH ENDS Fig.3.15 shows a solid circular, shaft fixed at both ends. Let l - Length of the fixed shaft. W - Point load lʹ - Length of bar right angles to the fixed bar Then, deflection due to bending of the bar is given by Deflection due to rotation is given by ⸫ Total deflection of the shaft fixed at both ends is given by Example 3.45 A horizontal, steel bar of 50 mm diameter and 1000 mm length is fixed at both ends. A rigid bracket is fixed to the middle of the bar, at right angles to its axis which have a length of 300 mm and in the same horizontal plane containing the axis of the bar, Determine the deflection of the shaft if the vertical load in the bracket is 1500 N. Take E = 2 × 105 N/mm2 and C = 7.6 × 101 N/mm2. Given: To find: Deflection (δ) of the fixed shaft.
Solution: And, deflection due to rotation is, Result: The deflection of fixed shaft, δ = 0.847 mm
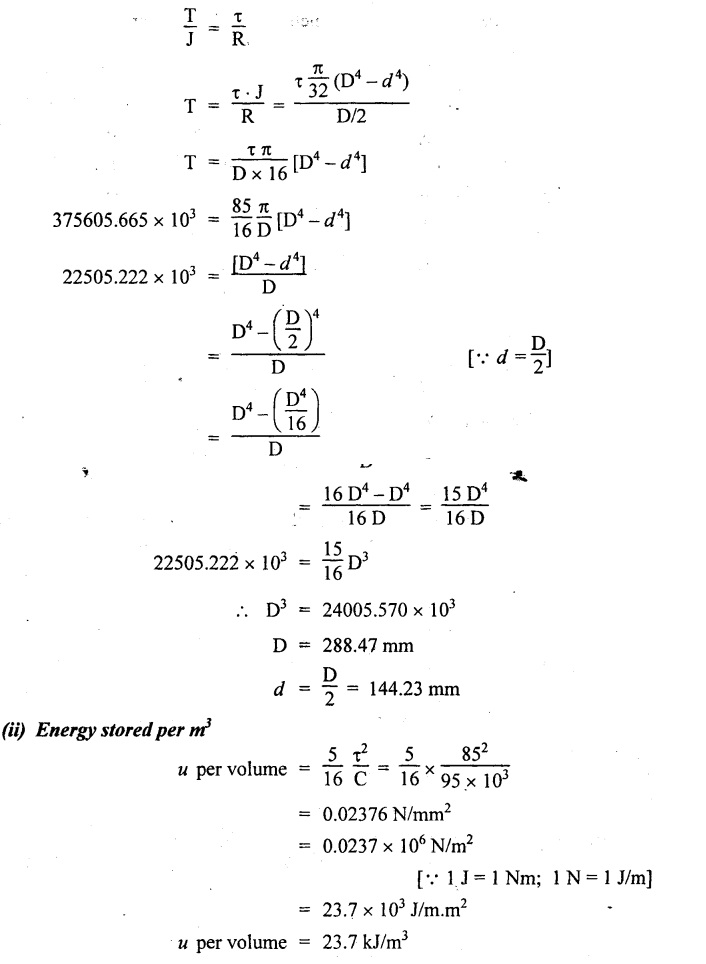
For solid shaft: Consider a solid circular shaft of length and radius R, subjected to a torque T producing a twist θ in the length of the shaft. Substitute the above in work done equation, Example 3.46 Show that the strain energy stored per unit volume of the shaft is Given: To find: (i) Shaft diameter (ii) Energy stored per m3 of volume Solution: Result: Shaft diameter, D = 288.47 mm d = 144.23 mm Strain energy per volume = 23.7 kJ/m3 Compare the strain energies of the hollow and solid shafts subjected to the same maximum shear stress in torsion. The outer diameter is n times the inner diameter. Masses, lengths and materials of the two shafts are same. Given: To find: Strain energies of hollow and solid shaft. Solution: For the same mass, Result: ⸫ The hollow shaft has more strain energy as compared to a solid shaft.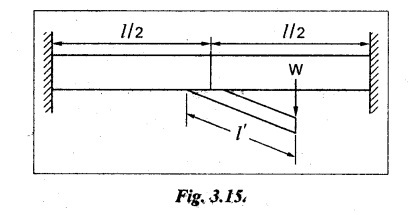
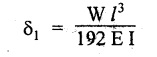
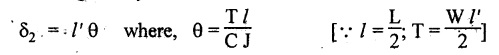
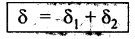
SOLVED PROBLEMS



STRAIN ENERGY DUE TO TORSION

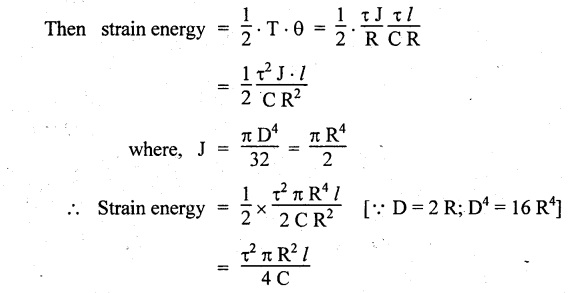

SOLVED PROBLEMS
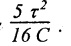 If the external diameter of a hollow shaft is twice the internal 16 C diameter and it is subjected to pure torque and it attains a maximum shear stress t. Such a shaft is required to transmit 5900 kW at 150 rpm with uniform torque, the maximum stress not exceeding 85 MN/m2. Take C = 95 GN/m2. Find out the shaft diameters and the energy stored per of m3 volume.
If the external diameter of a hollow shaft is twice the internal 16 C diameter and it is subjected to pure torque and it attains a maximum shear stress t. Such a shaft is required to transmit 5900 kW at 150 rpm with uniform torque, the maximum stress not exceeding 85 MN/m2. Take C = 95 GN/m2. Find out the shaft diameters and the energy stored per of m3 volume.
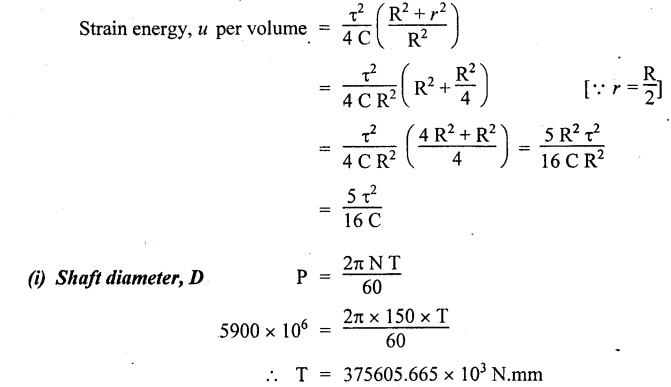
Example 3.47



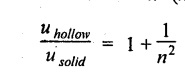
Strength of Materials: Unit III: Torsion : Tag: : Torsion - Strength of Materials - deflection of shaps fixed at both ends
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
