Matrices and Calculus: Unit IV: Integral Calculus
Definite Integral (Rectangle Method of Finding Area)
Worked Examples, Fundamental Theorem of Calculus
Each of these sums is called a Riemann sum.
DEFINITE INTEGRAL (RECTANGLE METHOD OF FINDING AREA) Let f be a continuous function on the closed interval [a, b], except possibly at a finite number of points, and bounded everywhere in [a, b]. If [a, b] is divided into n equal parts, each of length Then, the definite integral is defined as, Therefore area of rectangle in the first subinterval with height f(x0) and with Δx is f(x0). Δx. Similarly the area over the other intervals with f(x1), f(x2)... f(xn-1) as height, will be f(x1) Δx, f(x2) Δx, ........., f(xn-1) Δx. ⸫ The sum of the areas of these rectangles will be Now let us find the values of f at the right end of each subinterval − f(x1), f(x2)... f(xn) with these values as height and Δx as width the sum of the areas of the rectangles is If An is the area under the curve with n rectangles then sn < An < Sn Now Each of these sums is called a Riemann sum. Limit of Σ is the symbol ∫ obtained by stretching Σ. f(x) is called the integrand and the numbers a, b are the limits of integration, dx indicates the variable of the function being integrated is x. For example: Since both represent area under the graph of ƒ from a to b, the value, of the integrals be the same. Since the name of the variable x or t does not affect the value of the integral, x or t is called a dummy variable. Note: The above proof is geometrical in nature. The rigorous proof is beyond the scope of this book. Example 1 If f(x) = x2 – 2x, x ∈ [0,3] evaluate the Reimann sums with n = 6 at the left end point of the subintervals and at the right end points. Solution Given f(x) = x2 – 2x, x ∈ [0,3] with n = 6 Right end Reimann sum is But f(3) 32 - 2.3 = 9 – 6 = 3 All other values are there above. Example 2 Evaluate Solution Divide the interval [a, b] into n equal parts by the points a = x0, x1,..., xn = b, each of width Here f(x) = x2. We notice that even for this simple function f(x) = x2 the computation of area under the curve as a definite integral is difficult. This limit can be evaluated in certain cases only. For this reason, the progress on the area problem remained at an elementary level until the latter part of the 17th centuary when Issac Newton and Leibnitz independently discovered the fundamental relationship between the area under a curve or the definite integral and the derivative. This relationship is given by the Fundamental theorem of calculus, appropriately named because it establishes a connection between the two branches of calculus: differential calculus and integral calculus. Theorem 4.1 If f is continuous on [a, b], then 1. The function F defined by F(x) = 2. Note: Part (1) of the theorem says Part (2) says Since F'(x) represents the rate of change of F(x) w. r. to x, So, part 2 of the theorem is known as net change theorem We write 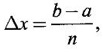 using the points of division
using the points of division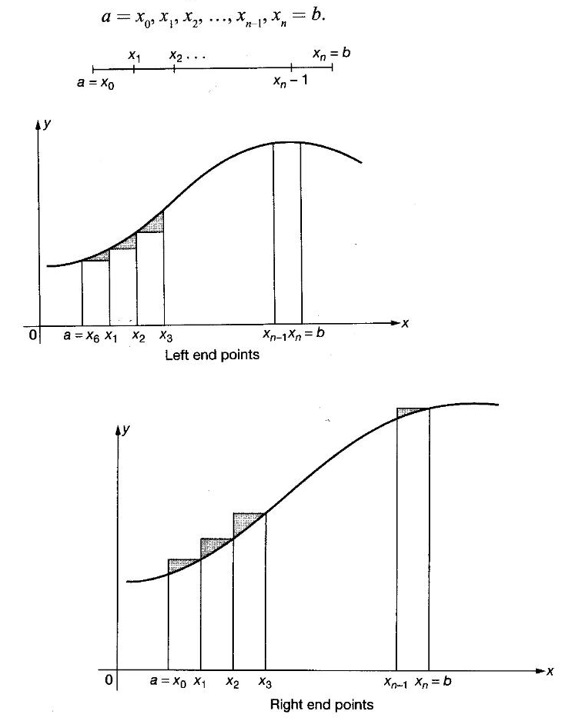

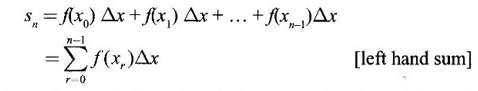
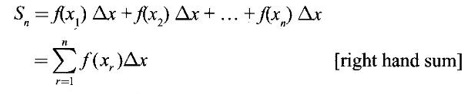


WORKED EXAMPLES

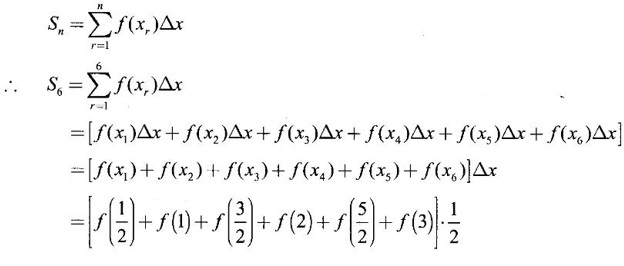
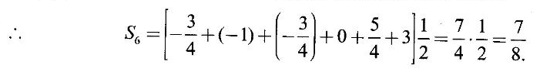
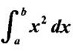 as limit of sum.
as limit of sum.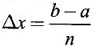

Fundamental Theorem of Calculus
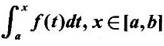 and differentiable in (a, b) and F'(x) = f(x).
and differentiable in (a, b) and F'(x) = f(x).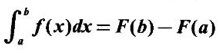

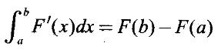
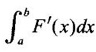 is the net change of F on [a, b] and the net change is F(b) - F(a).
is the net change of F on [a, b] and the net change is F(b) - F(a).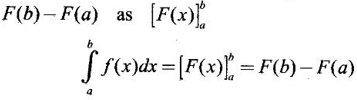
Matrices and Calculus: Unit IV: Integral Calculus : Tag: : Worked Examples, Fundamental Theorem of Calculus - Definite Integral (Rectangle Method of Finding Area)
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
