Theory of Machines: Unit IV: Force Analysis
correction couple
Force Analysis - Theory of Machines
From Section 11.5, we know that a rigid body of mass m can be replaced by two dynamically equivalent masses satisfying the three conditions.
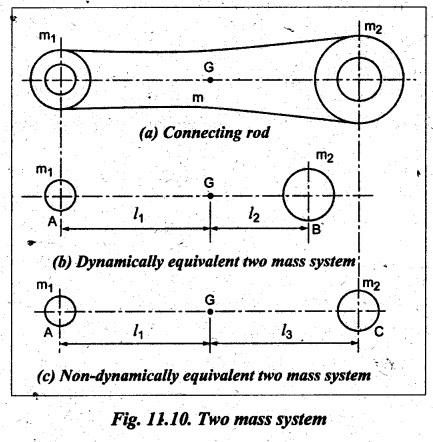
CORRECTION COUPLE From Section 11.5, we know that a rigid body of mass m can be replaced by two dynamically equivalent masses satisfying the three conditions. But when considering the effect of the inertia of the connecting rod, it is convenient to place the masses arbitrarily. Then first two conditions of dynamic equivalence are satisfied, but the third condition is not satisfied. This means that the mass moment of inertia of both the masses placed arbitrarily will differ than that of mass moment of inertia of the rigid body. In order to satisfy the third condition of dynamic equivalence, it is necessary to apply some couple on the arbitrarily chosen two mass system. This couple is known as correction couple. Fig.11.10(a) shows a rigid body (say, a connecting rod) whereas Fig.11.10(b) shows the equivalent dynamical system (which satisfy the three conditions of dynamic equivalence). As shown in Fig.11.10(b), for the dynamically equivalent two mass system, two masses m1 and m2 are placed at points A and B respectively. Suppose, if we need to place the mass m2 at point C instead of B as shown in Fig.11.10(c), then the third condition of the dynamic equivalent will not be satisfied. In order to satisfy, we have to apply some correction couple so that the system becomes dynamically equivalent. Let m = Mass of the rigid body, k and I = Radius of gyration and mass moment of inertia of the dynamically equivalent system respectively, k1 and I1 = New radius of gyration and new mass moment of inertia of the non- dynamically equivalent system respectively, and α = Angular acceleration of the body We know that the torque required to accelerate the dynamically equivalent system, Similarly, the torque required to accelerate the non-dynamically equivalent system, The difference between the torque required to accelerate non-dynamically equivalent system (T1) and the torque required to accelerate the dynamically equivalent system (T) is known as the correction couple TC. Substituting these values in equation (iii), we get Thus this corrective couple TC must be applied, when the masses are placed arbitrarily to make the system dynamically equivalent. Note The value of correction couple is always positive, and its direction will be the same as that of angular acceleration α. Example 11.18 A small connecting rod 220 mm long between centers has a mass of 2 kg and a moment of inertia of 0.02 kg.m2 about its center of gravity. The center of gravity is located at a distance of 150 mm from the small end center. Determine the dynamically equivalent two mass systems when one mass is located at the small end center. If the connecting rod is replaced by two masses located at the two centers, find the correction couple that must be applied for complete dynamical equivalence of the system when the angular acceleration of the connecting rod is 20000 rad/s2 anticlockwise. l = 220 mm = 0.22 m; m = 0.22 m; m = 2 kg; I = 0.02 kg.m2; l1 = 150 mm = 0.15 m; α = 20000 rad/s2. Solution: Refer Fig.11.10. 1. Dynamically equivalent two mass system: We know that I = m k2 or 0.02 = 2 k2 or k = 0.1 m We know that for dynamically equivalent system, Let m1 = Mass placed at the gudgeon pin, and m2 = Mass placed at a distance l2 from C.G. 2. Correction couple: Since the connecting rod is replaced by two masses one at the gudgeon pin and the other at the crank pin, therefore Since the value of correction couple TC is positive, therefore the direction of correction couple is same as that of angular acceleration. i.e., anticlockwise.1. What is it?
2. Determination of Correction Couple


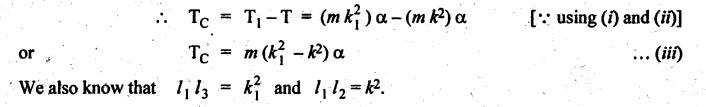
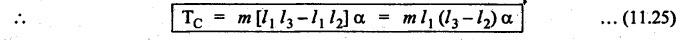
Given data: 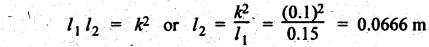
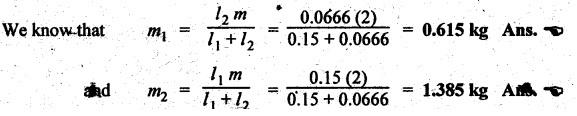

Theory of Machines: Unit IV: Force Analysis : Tag: : Force Analysis - Theory of Machines - correction couple
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
