Matrices and Calculus: Unit II: Differential Calculus
Continuity
Definition, Theorem, Solved Example Problems | Differential Calculus
Intuitively, a function is continuous at a point or continuous in an interval if its graph has no break at the point or in the interval.
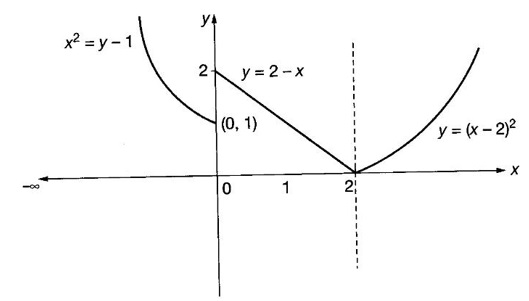
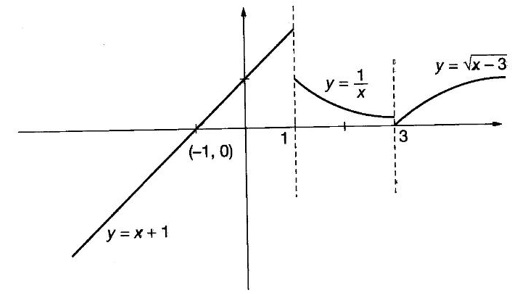
CONTINUITY Intuitively, a function is continuous at a point or continuous in an interval if its graph has no break at the point or in the interval. This idea is made precise by the following definition. Definition 2.14 A function f is continuous at a point a if The definition implies the following conditions (i) ƒ is defined at a i.e f(a) exists If any of these conditions fail, then the function ƒ is not continuous at the point a or discontinuous at a. Sometimes the continuity may be on one-side only i.e., one sided continuity. Definition 2.15 A function fis said to be continuous from the right at a(or right continuous at a) if f is said to be continuous from the let at a(or left continuous at a) if Definition 2.16 lim f(x) = f(a) A function f is said to be continuous in an open interval (a, b) if f is continuous at every point in (a, b) A function is said to be continuous on a closed interval [a, b] if (i) f is continuous in the open interval (a, b) A continuous function is one that is continuous at every point in its domain. It need not be continuous on every interval. A function is discontinuous in an interval if it is discontinuous in at least one point in the interval. As continuity is defined in terms of limit, the basic limit theorem holds for continuous functions also. Theorem 2.5 Let the functions ƒ and g be continuous at the point a, then the following functions are continuous at a (i) ƒ+g (ii) ƒ-g (iii) fg (iv) (v) cf, where c is a constant We now list some standard functions which are continuous (in their domain) 1. Any polynomial p(x) is continuous 2. Any rational function 3. ex and log ex are continuous 4. trigonometric and inverse trigonometric functions are continuous In applications the theorem will be used for these functions For example, ex + sin x is continuous for all x ∈ (-∞, ∞). Theorem 2.6 If Theorem 2.7 If g is continuous at a and ƒ is continuous at g(a), then ƒ · g is continuous at a Proof: Since g is continuous at a, ⸫ f · g is continuous at a An important property of continuous function is the intermediate value theorem given below Theorem 2.8 Let f be a continuous function on a closed interval [a, b] and d be any number between ƒ(a) and ƒ(b), where f(a) ≠ f(b). Then there exists a point c is (a, b) such that f(c) = d. We list now some more properties of continuous functions 1. If f is a continuous functions on the closed interval [a, b] and ƒ(a) and f(b) have opposite signs, then there exists at least one point c ∈ (a, b) such that f(c) = 0 2. If f is a continuous function on the closed interval [a, b], then f attains its greatest and least values at some points c and d in [a, b]. It is known as extreme value theorem. 3. A continuous function on the closed interval [a, b] will take on every value between its maximum and minimum values at least once. Test the continuity of the following examples. Example 1 Solution We have to test for continuity at a = 1 Here ƒ is discontinuous at x = 1 Example 2 Solution We have to test continuity at x = 3 Hence f is discontinuous at x = 3 Example 3 Solution We have to test continuity at x = 0. So, we find the left and right limits ⸫ the function f is discontinuous at x = 0 Note: Domain of ƒ is (−∞, ∞) In (-∞, 0), ex is continuous In (0, ∞), x2 is continuous Since ⸫ In (-∞, ∞), ƒ is discontinuous, as ƒ is discontinuous at x = 0 Example 4 Solution We have to test continuity at x = 0 So f is discontinuous at x = 0 In Examples (5) and (6) below find the points at which ƒ is discontinuous. At which of these points is f continuous from the right, from the left or neither. Also sketch the graph of ƒ. Example 5 Solution Here f is defined for all x ∈ (-∞, ∞) The points x = 0 and x = 2, divide the number line into three intervals (-∞, 0), (0, 2), (2, ∞). In each of these open intervals f(x) is a polynomial and hence continuous. We shall test for continuity at x = 0 and x = 2 So, f is continuous on the left at x = 0. Hence f is discontinuous at x = 0 At x = 2 and f(2) = 2 – 2 = 0 Hence ƒ is continuous at x = 2 Thus f is continuous ∀x∈(-∞, ∞), except x = 0 We shall now draw the graph of ƒ In the interval (-∞, ∞), the graph is y = 1 + x2, which is a parabola x2 = y - 1 [of the form x2 = 4ay] with vertex (0, 1) and the axis is x = 0 i.e., the y-axis and upward. In the interval (2, ∞), the graph is y = (x - 2)2, which is a parabola [of the form x2 = 4ay] with vertex (2, 0), axis is the line x = 2 and upward. With these information we draw the graph Example 6 Solution Here ƒ is defined for all x ∈ (-∞, ∞) The points x = 1 and x = 3 divide the real line into 3 intervals (-∞, 1), (1, 3) and (3, ∞) In each of these open intervals the function f is continuous being polynomial, rational function and square root function. So, we test for continuity at the points x = 1 and x = 3 At x = 1 Hence f is continuous on the left at x = 1. Hence, the function is continuous on the right at x = 3. Hence, ƒ is discontinuous on the left at x = 3 ⸫ f is discontinuous at x = 3 Thus f is continuous ∀x ∈ (-∞, ∞), except at x = 1 and x = 3. So, f is discontinuous. We shall now draw the graph to visualize the function. In the interval (-∞, 1) the graph is y = x + 1 which is a straight line When x = 0, y = 1 and when y = 0, x = -1 ⸫ two points on the line are (0, 1)(−1, 0) In the interval (1, 3), the graph is which is a rectangular hyperbola. In the interval (3, ∞), the graph is which is a parabola, [of the form y2 = 4ax] with vertex (3, 0), and the axis is y = 0, the x-axis and the curve is towards the positive x-axis. With these informations we draw the graph. Example 7 For what value of a is Solution Example 8 For what value of c, is the function continuous on (-∞, ∞)? Solution Suppose f is continuous for all x ∈ (-∞, ∞) Then in particular, f is continuous at x = 2 Example 9 Solution So, in particular, f is continuous at x = -1 and x = 1 Solve (1) and (2), a − b = 4 Adding 2a = 16 ⇒ a = 8 ⸫ b = 12 - a = 12 – 8 = 4 ⸫ a = 8, b = 4 Example 10 Solution and f(x) is continuous for all real x. So, in particular, f is continuous at x = 2 and x = 3. ⸫ 9a - 3b + 3 = -a + b + 6 ⇒ 10a - 4b = 3 (2) Solve (1) and (2) to find a and b. (1) × 2 ⇒ 8a - 4b = 2 (2) is 10a - 4b = 3 Subtracting, Substituting in (1), we get Example 11 Find the values of a, b, c for which the function is continuous at x = 0 Solution Suppose ƒ is continuous at x = 0 = 1(a + 1) + 1 = a + 2 Example 12 Show that |x| is continuous ∀x∈ (−∞, ∞) Solution Hence For all x < 0 and x > 0 the function is a first degree polynomial and hence continuous. ⸫ f is continuous everywhere. i.e., ƒ is continuous on (−∞, ∞). Example 13 Solution Hence, f is continuous everywhere Example 14 Show that f(x) = 1 - Solution Given f(x) = 1 − To prove ƒ is continuous in the closed interval [-1, 1]. So, we have to prove f is continuous (i) in the open interval (-1, 1) (ii) Right continuous at x = -1 (iii) Left continuous at x = 1 (i) Let a ∈ (-1, 1) be an arbitrary number i.e., -1 < a < 1 [⸪ square root function is continuous] ⸫ f is continuous at a and a is arbitrary in (−1, 1). So, f is continuous ∀a∈ (-1, 1). So, f is left continuous at x = 1 Hence, ƒ is continuous on [−1, 1] A function f which is not continuous at a point a is discontinuous at a. Discontinuity at a can occur in the following ways. (i) f is not defined at a (ii) (iii) The discontinuity of the type (iii) is called a removable discontinuity because it can be removed by redefining the value of f(a). So, f is discontinuous at x = 1. Suppose we redefine the value f(1) = 2 then f is continuous. So, by redefining the value of ƒ at x = 1, we have removed the discontinuity. Hence x = 1 is a removable discontinuity of f. The discontinuity of type (ii) can happen in different ways Discuss the continuity of the following functions 1. Continuous 2. Continuous 3. Continuous, except at x = 0 4. Continuous 5. Continuous, except at x = 0 6. Continuous 7. Continuous, except at x = 0 8. Continuous 9. Continuous 10. Continuous 11. Continuous 12. Continuous, except at x = 0 13. 8/5 14. -2,3 15. 0, -2 16. a = 5/2, b = -3/2 17. 7 18. A = -1, B = 1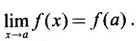



Continuity in an interval


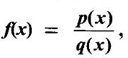 where p(x) and q(x) are polynomials, is continues
where p(x) and q(x) are polynomials, is continues and f is continuous at b then
and f is continuous at b then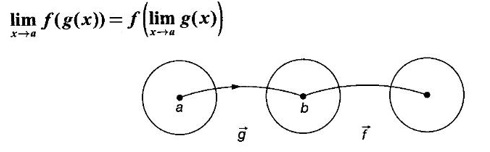
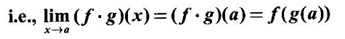
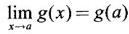 and ƒ is continuous at b = g(a)
and ƒ is continuous at b = g(a)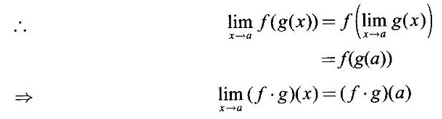
WORKED EXAMPLES

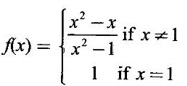
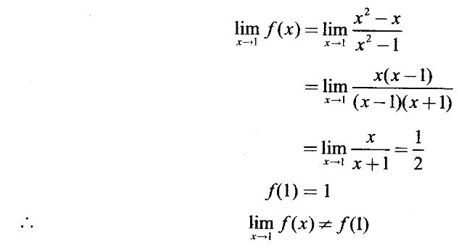

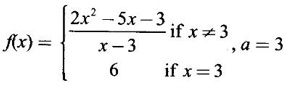
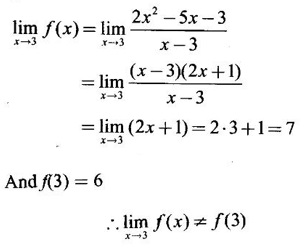

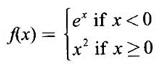
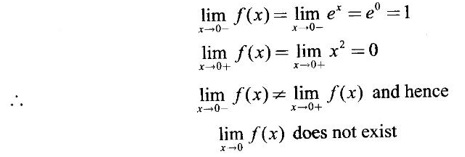
 ƒ is right continuous at x = 0
ƒ is right continuous at x = 0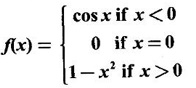

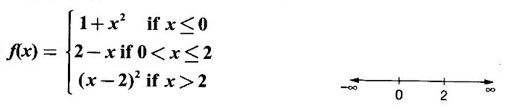
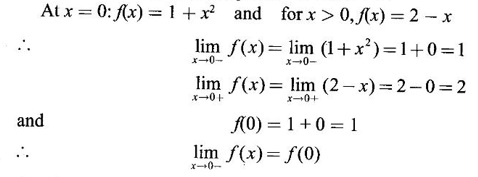

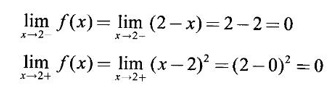
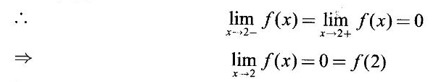

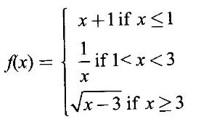
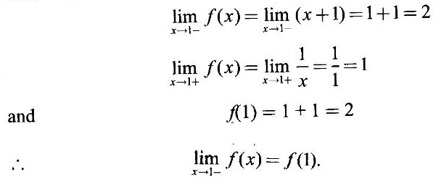


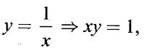


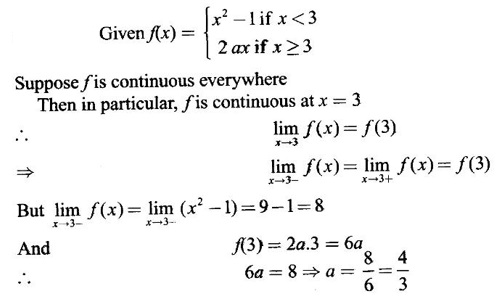
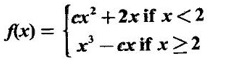
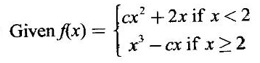




 is continuous for all real x, then find the values of a and b.
is continuous for all real x, then find the values of a and b.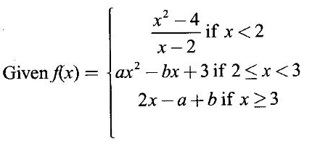



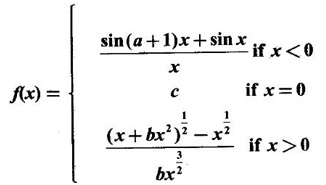



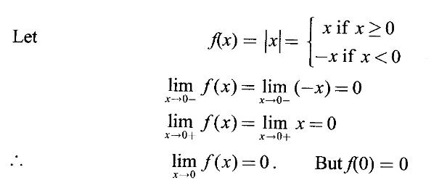
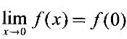 and so the function is continuous at x = 0.
and so the function is continuous at x = 0.

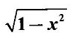 is continuous in the interval [−1, 1]
is continuous in the interval [−1, 1]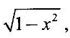 x∈[−1, 1]
x∈[−1, 1]
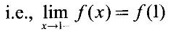


1. Types of Discontinuity
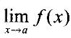 does not exist
does not exist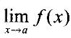 exists and ƒ(a) exists, but they are not equal
exists and ƒ(a) exists, but they are not equal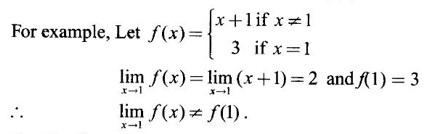
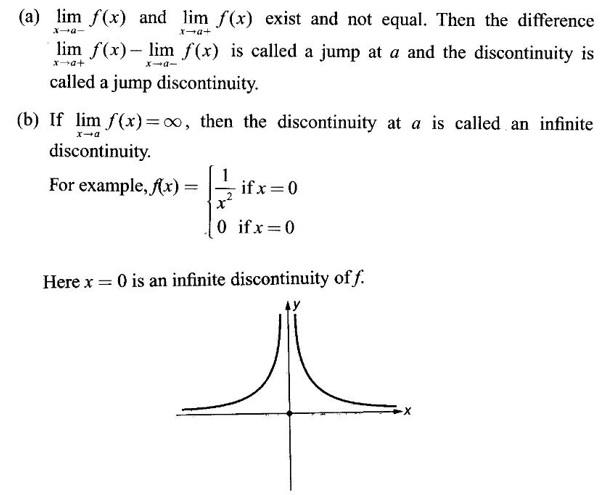
EXERCISE 2.4

ANSWERS TO EXERCISE 2.4
Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Theorem, Solved Example Problems | Differential Calculus - Continuity
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
