Engineering Graphics: Unit I (d): Engineering Curves
Construction of Spiral Curves
Engineering Graphics (EG)
Spiral is a curve generated by a point moving continuously in one direction along a straightline while the straightline revolves about a fixed point.
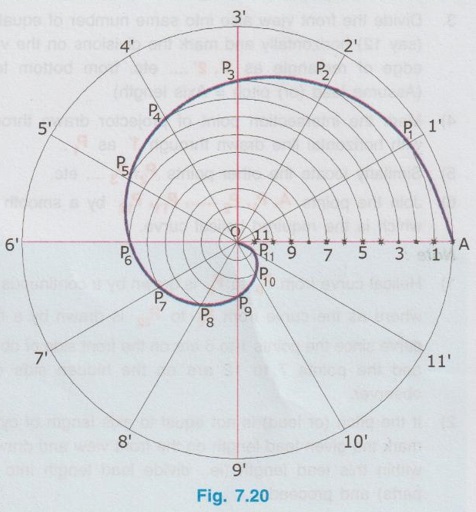
SPIRAL CURVES Spiral is a curve generated by a point moving continuously in one direction along a straightline while the straightline revolves about a fixed point. The fixed point about which the line revolves is called pole and the line joining any point on the curve and the pole is known as the radius vector. One complete revolution of the spiral forms one convolution. Two types of spiral curves are : i) Archimedes spiral ii) Logarithmic spiral Data known : (i) Radius (ii) Number of convolutions Example 10: Draw an Archimedian spiral of one convolution given the radius as 60mm. Procedure: 1) Mark a point O and draw a circle of radius 60mm. 2) Draw horizontal diameter, and mark the intercept of horizontal diameter with the circle at A. When the line OA revolves about O for one revolution, point A moves uniformly to O. 3) Divide the line OA and the circle into same number of equal parts (say 12), marking the divisions as 1, 2 etc., on AO from A and 1', 2' etc. on the circumference of circle from A in anticlockwise direction. 4) When the line OA revolves 1/12 of a revolution, (ie., from 0-A to 0-1'), A moves towards O by a distance equal to 1/12 AO. Hence to get the position of A on 0-1', draw an arc with O as centre and 0-1 as radius to cut the radial line 0-1' at P1. 5) Similarly obtain the points P2, P3.... etc., by taking O as centre and O-2, 0-3... etc. by radius to cut the radial lines 0-2, 0-3'.... etc. respectively. 6) Join the points A, P1, P2 .... P11 and O by a smooth curve which is the required spiral curve.1. Construction of Archimedes spiral
Engineering Graphics: Unit I (d): Engineering Curves : Tag: : Engineering Graphics (EG) - Construction of Spiral Curves
Engineering Graphics: Unit I (d): Engineering Curves
Under Subject
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation