Engineering Graphics: Unit I (d): Engineering Curves
Construction of Hypocycloid
Engineering Graphics (EG)
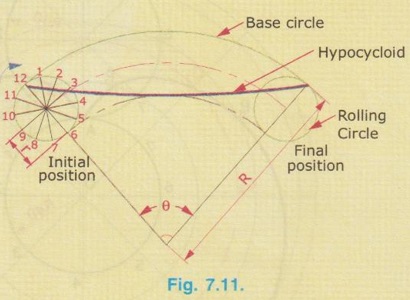
Hypocycloid is a curve generated by a point on the circumference of a circle known as rolling circle which rolls without slipping on the inside of an another circle known as Base circle.
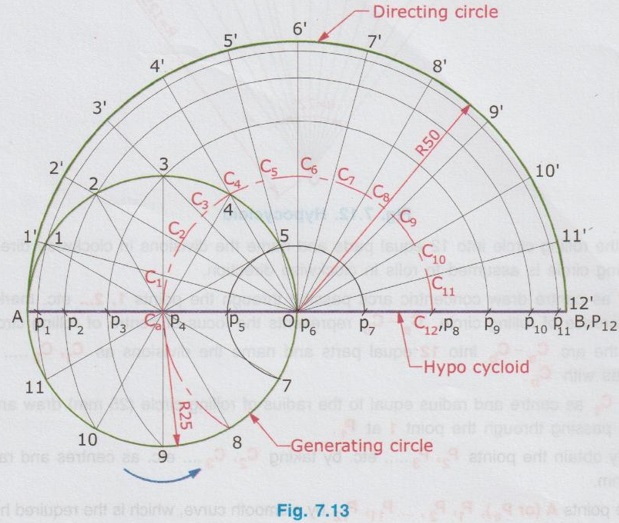
CONSTRUCTION OF HYPOCYCLOID Hypocycloid is a curve generated by a point on the circumference of a circle known as rolling circle which rolls without slipping on the inside of an another circle known as Base circle. 1) Rolling circle rolls on the inside of Base circle. 2) The diameter of rolling circle is less than the diameter of base circle. 3) In construction of hypocycloid, if the rolling circle is assumed to roll inside of base circle in clockwise direction, name the divisions on the circumference of circle also in clockwise direction from the point of contact. 4) The method for constructing hypocycloid is the same as for epicycloid other than the difference mentioned in the point (3). 5) Note that if the radius of the base circle is twice the radius of the rolling circle then the hypocycloid is a straight line since θ = r/2r × 360 = 180°. Example 4: Construct a hypocycloid of a point on the circumference of a rolling circle of diameter 50 mm which rolls inside of an another circle of diameter 250 mm. Also draw tangent and normal at a point M on the curve. 1) Mark a point O, centre of base circle. 2) Taking the point 'O' as centre and radius 125 mm (radius of base circle) draw an arc which subtends an angle θ = 72° at O, 3) Mark a point A on the arc and join with O. 4) Mark an another point B on the arc such that ∠AOB = 72° and join with O. Clearly length of arc = Distance travelled by the rolling circle for one revolution = circumference of rolling circle. 5) Mark a point Ca on the line AO such that A - Ca = radius of rolling circle (25 mm) and Ca – O = (R-r) = (125-25) = 100 mm. 6) Taking Ca as centre and radius 25 mm draw the rolling circle, on the inside of base circle. 7) Divide the rolling circle into 12 equal parts and name the divisions in clockwise direction since the rolling circle is assumed to rolls in clockwise direction. 8) With O as centre draw concentric arcs passing through the points 1, 2... etc. marked on the circumference of rolling circle. Ca - Cb represents the locus of centre of rolling circle. 9) Divide the arc Ca - Cb into 12 equal parts and name the divisions as C1, C2..... etc. C12 coincides with Cb. 10) Taking C1 as centre and radius equal to the radius of rolling circle (25 mm) draw an arc to cut the arc passing through the point 1 at P1. 11) Similarly obtain the points P2, P3..... etc. by taking C2, C3 .... etc. as centres and radius equal to 25 mm. 12) Join the points A (or Po), P1, P2, …. P11, P12 by a smooth curve, which is the required hypocycloid. Let M be the point on Epicycloid through which tangent and normal are to be drawn. i) With M as centre and radius equal to 25 mm (radius of rolling circle) draw an arc to cut the arc bns Ca - Cb at C'. ii) Join C' and centre of base circle O and extend it to intersect the arc AB at N. iii) Join M and N and extend it to N'. NN' is the required normal. iv) Draw a line perpendicular to NN' and passing through M. Let this line be TT' which is the required tangent drawn through the point M. Example 5: A circle of radius 25mm rolls on the inside of another circle of radius 50mm in clockwise direction. Draw the path traced by a point on the rolling circle. Here the generating circle rolls inside the circle, hence the path traced by a point on the circumference of generating circle is hypocycloid. Angle subtended, θ = r/R × 360 = 25/50 × 360 = 180° 1) Mark a point O and with O as centre, draw a line (say horizontal line) OA of length 50mm, equal to diameter of generating circle. 2) Locate the midpoint of OA at Ca, centre of generating circle. 3) With Ca as centre and radius 25mm draw rolling circle and divide the circumference into any number of equal parts (say 12). Name the divisions as 1, 2.... etc. in clockwise direction. (since generating circle rolls in clockwise direction). 4) Extend AO line and mark B such that OA = OB = 50mm, so that the angle subtended is 180°. 5) With O as centre draw concentric arcs passing through the point A, 1, 2.... etc. Also draw the locus of centre of generating circle to cut OB line. 6) Divide the angle subtended at O (ie., 180°) also into same number of equal parts (say 12) and draw the radial lines to cut the arc passing through A at 1', 2'.... etc., Let these lines intersects the locus of centre of generating circle at C1, C2 … etc., 7) Now with C1 as centre and radius equal to 25mm (radius of generating circle) draw an arc to cut the arc passing through the point 1 at P1. 8) Similarly obtain the points P2, P3… by taking C2, C3 .... etc., as centres and cutting the arcs passing through 2, 3..... etc. 9) Join the points A, P1, P2 …., P11, P12 by a smooth curve which is the required hypocycloid. (Note: Hypocycloid is the straightline AB, since θ = 180°. Also note that P6 coincides with O and P12 coincides with B).Points to understand
Construction:

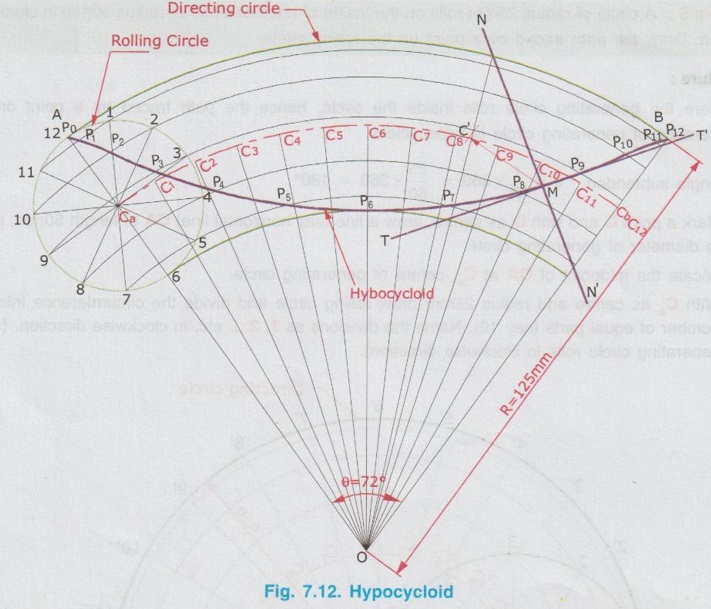
To draw tangent and normal at a point M.
Procedure:
Engineering Graphics: Unit I (d): Engineering Curves : Tag: : Engineering Graphics (EG) - Construction of Hypocycloid
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
