Engineering Graphics: Unit I (d): Engineering Curves
Construction of Epicycloid
Engineering Graphics (EG)
Epicycloid is a curve generated by a point on the circumference of a circle which rolls on an another fixed circle.
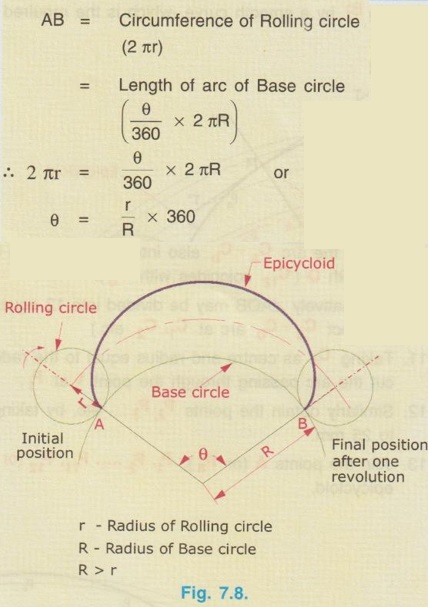
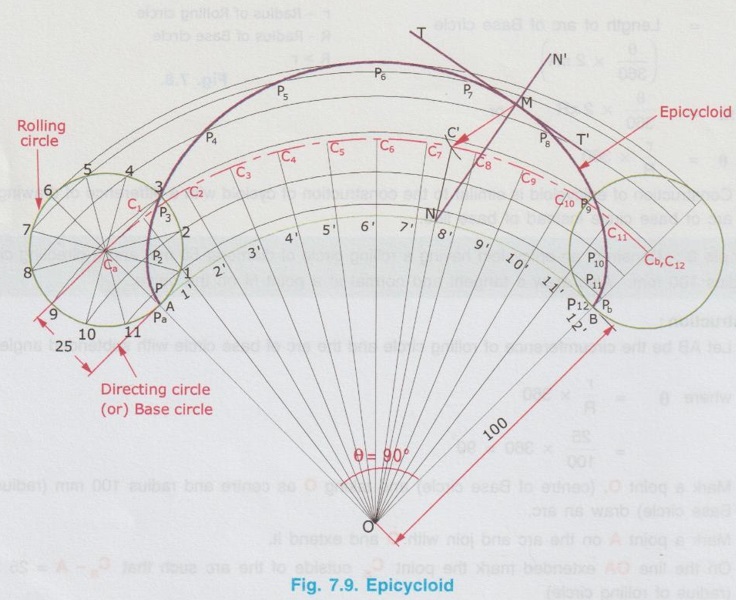
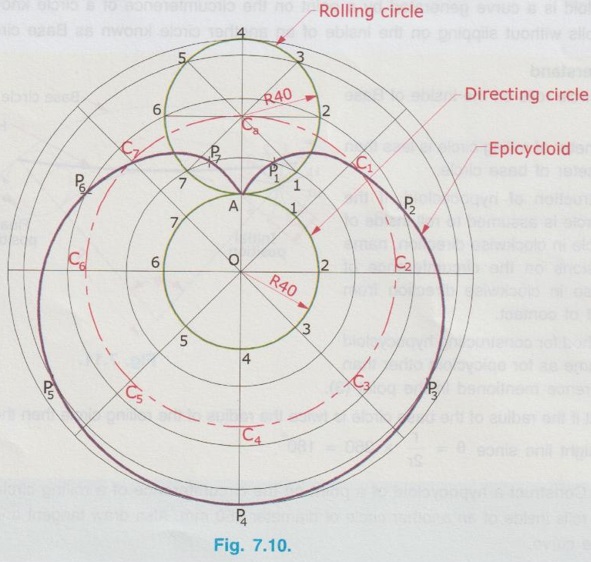
CONSTRUCTION OF EPICYCLOID Epicycloid is a curve generated by a point on the circumference of a circle which rolls on an another fixed circle. The circle which rolls is known as rolling circle and the circle which is fixed is known as Base circle or Directing circle. 1. Rolling circle rolls on the outside of Base circle. 2. Normally the diameter of rolling circle is less than the diameter of base circle. 3. Distance travelled by the rolling circle for one revolution is equal to its circumference, which is equal to length of an arc of Base circle as shown below. 4. Construction of epicycloid is similar to the construction of cycloid with a difference of drawing an arc of base circle instead of base line. Example 2: Construct an epicycloid having a rolling circle of diameter 50 mm and a directing circle of radius 100 mm. Also draw a tangent and normal at a point M on the curve. 1. Let AB be the circumference of rolling circle and the arc of base circle with subtended angle θ. where θ = r / R × 360 = 25 / 100 × 360 = 90° 2. Mark a point O, (centre of Base circle) and taking O as centre and radius 100 mm (radius of Base circle) draw an arc. 3. Mark a point A on the arc and join with O and extend it. 4. On the line OA extended mark the point Ca outside of the arc such that Ca - A = 25 mm (radius of rolling circle) 5. With Ca as centre and 25 mm as radius draw a circle which represents the initial position of rolling circle. 6. Divide the rolling circle into 12 equal parts and name the divisions as 1, 2... etc. in anticlockwise direction (assuming that the rolling circle rolls in clockwise direction). 7. Mark a point B on the arc of base circle such that ∠AOB = 90°. 8. Join the points B and O and extend it. 9. With O as centre draw concentric arcs passing through the points 1, 2,.... etc. marked on the circumference of rolling circle. Ca - Cb represents the locus of centre of rolling circle. 10. Divide the arc Ca - Cb also into 12 equal parts and name the divisions as C1, C2... etc. and join with O (C12 coincides with Cb). (Alternatively ∠AOB may be divided into 12 equal parts and draw lines through these points to intersect Ca - Cb arc at C1, C2 etc.) 11. Taking C1 as centre and radius equal to the radius of rolling circle (= 25 mm) draw an arc to cut the arc passing through the point 1 at P1. 12. Similarly obtain the points P2, P3.... etc. by taking C2, C3.... etc. as centres and radius equal to 25 mm. 13. Join the points A (or Pa), P1, P2 … P11, P12 (or B) by a smooth curve, which is the required epicycloid. Let M be a point on epicycloid through which tangent and normal are to be drawn. i) With M as centre and radius equal to 25 mm (radius of rolling circle) draw an arc to cut the Ca - Cb arc at C'. ii) Join C' and centre of base circle O to intersect the arc AB at N. iii) Join M and N and extend which is the required normal, NN'. iv) Draw a line perpendicular to NN' and passing through M. Let this line be TT', which is the required tangent to the epicycloid drawn through the point M. Example 3: Construct an epicycloid with the radius of rolling circle and the radius of directing circle equal to 40 mm. Here radius of rolling circle (r) and the radius of directing circle (R) are equal to 40mm. Hence, subtended angle between the circumference of rolling circle and arc of base circle, which indicates the initial position and the final position of rolling circle after one complete revolution remains the same. ie., the epicycloid is a closed one in this particular case. 1. With O as centre and 40mm radius draw the directing circle. 2. Draw vertical diameter and mark the intersection with the circumference of circle at A. 3. Extend OA line, mark the point Ca outside of the arc such that Ca - A = 40 mm, equal to radius of rolling circle. 4. With Ca as centre and 40mm radius draw a circle. 5. Divide the rolling circle into any number of equal parts (say 8) and mark the divisions as 1, 2, …. etc. in anticlockwise direction (assuming the rolling circle rolls in clockwise direction). 6. With O as centre draw concentric circles passing through the points 1, 2, .... etc. marked on the circumference of rolling circle. Also draw the locus of centre of rolling circle, taking O as centre and O - Ca as radius. 7. Divide the generating circle also into same number of equal parts (say 8) and mark the divisions as 1', 2'.... etc., on the circumference on generating circle. 8. Join the points 1', 2'.... etc., with the centre of generating circle O and extend to cut the locus of centre of rolling circle at C1, C2.... etc. 9. With 40mm as radius (ie., radius of rolling circle Ca - A) and C1 as centre cut the circle passing through 1 at P1. 10. Similarly obtain the points P2, P3.... etc. by taking C2, C3…. etc. as centres and cutting circles passing through the points 2, 3.... etc. 11. Join the points A, P1, P2 …. P7, A by a smooth curve, which is the required epicycloid.Points to understand
Construction :
To draw a tangent and normal at a point M
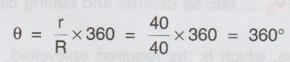
Engineering Graphics: Unit I (d): Engineering Curves : Tag: : Engineering Graphics (EG) - Construction of Epicycloid
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
