Engineering Physics: Unit I: Mechanics
Conservation of Angular Momentum
The law of conservation of angular momentum states that in the absence of an external torque, the angular momentum of a body or a system of bodies remains conserved.
CONSERVATION OF ANGULAR MOMENTUM The law of conservation of angular momentum states that in the absence of an external torque, the angular momentum of a body or a system of bodies remains conserved. The equation of motion of angular momentum of a particle is given by where If there is no torque i.e. or i.e., angular momentum is conserved. Thus, when the resultant external torque acting on a particle is zero, the total vector angular momentum of the particle remains conserved. This is called law or principle of conservation of angular momentum. Hence, in the absence of any external torque, if the moment of inertia (I) of the system increases, the angular velocity (ω) decreases. Similarly, if moment of inertia (I) decreases, the angular velocity increases. ( ⸪ angular momentum, L = I ω) Final angular momentum = Initial angular momentum i.e Angular momentum remains unchanged. If the moment of inertia I of a body changes due to redistribution of mass about the axis, angular velocity ω changes in such a manner that the product I ω remains a constant. It is clear that if the M.I. increases, the angular velocity ω decreases and vice versa. This principle of conservation of angular momentum is utilised by a diver, a skater, or a circus acrobat, while doing various acts of spinning. (i) Consider a man holding a pair of dumb bells or weights in his outstretched arms extending and standing on a turn table capable rotating freely about a vertical axis passing through its centre. (Fig. 1.41). The table is set rotating with certain angular velocity. The dumb bells are brought nearer the axis of rotation. As a consequence, the moment of inertia of the system about the axis of rotation decreases and the angular velocity of the turn table increases. As the man extends out his arms the M.I, increases and the angular velocity of the turn table decreases to maintain the angular momentum a constant. (ii) In case of an acrobat in a circus, the acrobat leaves the swing with his arms and legs stretched. As soon as he leaves the swing, he possesses some angular momentum. When the acrobat pulls his hands and legs together inwards, his M.I decreases. Hence the angular velocity of the acrobat increases considerably and the acrobat rolls. The following table summarizes the analogies showing the quantities relating to linear motion and the corresponding quantities relating to rotational motion.
![]() is the torque acting on the particle and
is the torque acting on the particle and ![]() is the rate of change of angular momentum.
is the rate of change of angular momentum.![]() = 0
= 0![]() = 0
= 0![]() = constant .... (2)
= constant .... (2)Illustrations to explain the law of conservation of angular momentum
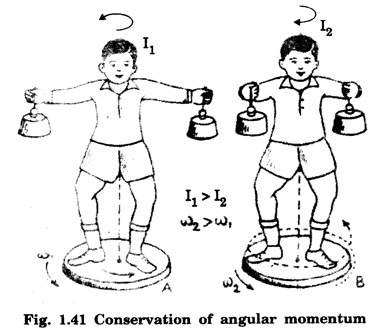
Analogies between linear and rotational motion
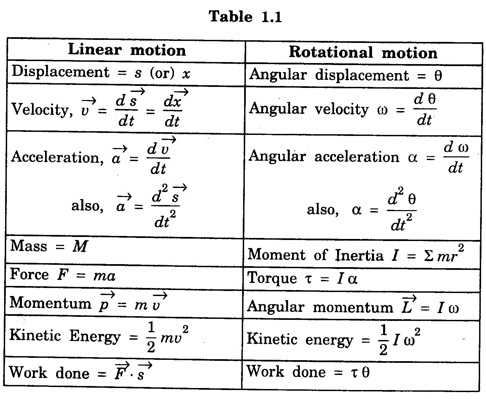
Engineering Physics: Unit I: Mechanics : Tag: : - Conservation of Angular Momentum
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
