conjugate profiles

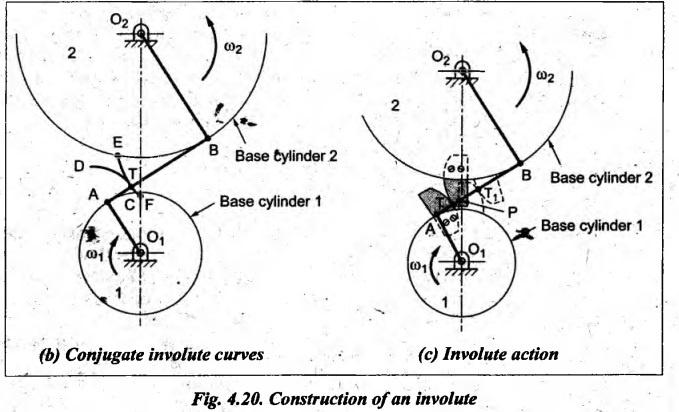
CONJUGATE PROFILES

• Two curves of any shape that fulfill the law of gearing can be used as the profiles of teeth. 

• If profile of the teeth of one of the mating gears is arbitrarily chosen and the profile of teeth of the other gear is determined so as to satisfy the law of gearing, such teeth are known as conjugate teeth.

• Gear profiles which can satisfy the law of gearing are known as conjugate profiles. 

1. Forms of Gear Tooth Profiles

• As discussed above, theoretically any suitable profile (i.e., curve) can be selected for gear tooth and a conjugate profile can be established for mating gear tooth.

• In other words, a large number of conjugate profiles are possible for making gears.

• But due to interchangeability aspect, cost and ease of production on larger scale, the different conjugate profiles are not employed in practice.

• The most common forms of tooth profiles widely used are:

1. Cycloidal tooth profile, and

2. Involute tooth profile.

• The above two forms of tooth profiles also satisfy the law of gearing.

2. Cycloidal Tooth Profile

• A cycloid is the curve traced by a point on the circumference of a circle which rolls without slipping on a fixed straight line, as shown in Fig.4.18(a).

• Epicycloid: When a circle rolls without slipping on the outside of a fixed circle, the curve traced by a point on the circumference of a circle is known as epicycloid.

• Hypocycloid: When a circle rolls without slipping on the inside of the fixed circle, then the curve traced by a point on the circumference of a circle is known as hypocycloid.

• Fig.4.18(b) illustrates the construction of epicycloid and hypocycloid curves. 

Construction of Cycloidal Gear Tooth Profile

• Fig.4.19 shows the construction of a tooth profile of a gear.

• When the rolling circle 2 rolls without slipping on the outside of the pitch circle and the point P on the circle 2 traces epicycloid PA, which represents the face of the cycloidal tooth.

• When the rolling circle 1 rolls without slipping inside of the pitch circle and the point P on the circle ces hypocycloid PB, which represents the flank of the tooth profile.

• The profile BPA is one side of the cycloidal tooth. Then the opposite side of the tooth B'P'A' is also traced as explained above.

3. Involute Tooth Profile

• An involute curve is the path generated by a tracing point on a cord as the cord is unwrapped from a cylinder called the base cylinder. 

Construction of an involute

• Fig.4.20(a) shows an involute generated by the tracing point T.

• Involute starts at tracing point T0 of the base cylinder and as the cord is unwrapped further, the involute T0TT1 is generated.

• It may be noted that the cord is the generating line and it is always normal to the involute. 

Proof to show that Two Mating Involute Tooth Profiles Satisfy Law of Gearing

Consider two gear blanks with fixed centres O1 and O2, having base cylinders with radii of O1A and O2B, as shown in Fig.4.20(b). It is assumed that a cord is wound clockwise around the base cylinder of gear 1, pulled tightly between points A and B, and wound counterclockwise around the base cylinder of gear 2. Now if the two base cylinders are rotated in the opposite directions so as to keep the cord tight, then a tracing point T traces out the involutes EF on gear 1 and GH on gear 2. Thus the involutes generated simultaneously by the single tracing point T are conjugate profiles.

Now assume that the cord is replaced by two plates having involute shapes which are fixed to the respective base cylinders, as shown in Fig.4.20(c). If gear 1 is rotated clockwise, gear 2 is caused to rotate counterclockwise. The path of contact is the line AB which is occupied earlier by the cord. Because the line AB is normal to both profiles at all points of contact and also line AB is always tangent to both base cylinders, therefore point P is the pitch point. Since the pitch point P does not move, therefore the involute curves are conjugate curves and satisfy the fundamental law of gearing.

4. Comparison between Involute and Cycloidal Tooth Gears

(Why are involute gears are universally used as compared to cycloidal gears?)

Table 4.2 compares the advantages, disadvantages, and applications of involute and cycloidal tooth gears.

Table 4.2, Involute tooth gears Vs Cycloidal tooth gears

Because of the above advantages (S.Nos. 2, 3 & 4), the involute gears are most commonly used in actual practice as compared to the cycloidal gears.