Theory of Machines: Unit III: Friction in Machine Elements
conical pivot bearing
Friction in Machine Elements - Theory of Machines
Consider a conical pivot shown in Fig.6.19.
CONICAL PIVOT BEARING Consider a conical pivot shown in Fig.6.19. Let W. = Axial load or load transmitted to the bearing surface, R = Radius of the shaft, 2α = Cone angle, P = Intensity of pressure normal to the cone, and μ = Coefficient of friction between shaft and bearing surface. When the pressure is assumed to be uniform over the bearing surface, then intensity of pressure is given by The total torque required to overcome the friction for the uniform pressure condition is given by We know that for uniform wear, Total torque required to overcome the friction for the uniform wear condition is given by Power lost overcoming friction is given by P = T • ω Example 6.15 A conical pivot bearing 150 mm in diameter has a cone angle of 120°. If the shaft supports an axial load of 20 kN and the coefficient of friction is 0.03, find the power lost in friction when the shaft rotates at 200 rpm, assuming (i) uniform pressure, and (ii) uniform wear. Given data: D = 150 mm or R = 75 mm = 0.075 m; 2α = 120° or α = 60°; W = 20 kN = 20 × 103 N; μ = 0.03; N = 200 rpm Solution: ω = 2πN/60 = 2 π (200)/60 = 20.94 m/s (i) Power lost in friction assuming uniform pressure: We know that frictional torque for uniform pressure condition, (ii) Power lost in friction assuming uniform wear: We know that frictional torque for uniform wear condition, Example 6.16 A conical pivot supports a load of 25 kN, the cone angle being 120°, and the intensity of normal pressure does not exceed 0.35 MPa. The external diameter is twice the internal diameter. Find the outer and inner radii of the bearing surface. If the shaft rotates at 180 rpm and the coefficient of friction is 0.05, find the power lost in friction assuming uniform pressure. [A.U., Nov/Dec 2009] Given data: W = 25 kN = 25 × 103 N; 2 α = 120° or α = 60°; p = 0.35 MPa = 0.35 × 106 N/m2; d1 = 2 d2 or r1 = 2 r2; N = 180 rpm; μ = 0.05. Solution: ω = 2πN/60 = 2 π (180)/60 = 18.85 rad/s Dimensions of the bearing: Let r1 and r2 = Outer and inner radii of the bearing surface. We know that intensity of normal pressure, Power absorbed in friction: Assuming uniform pressure, the total friction torque is given by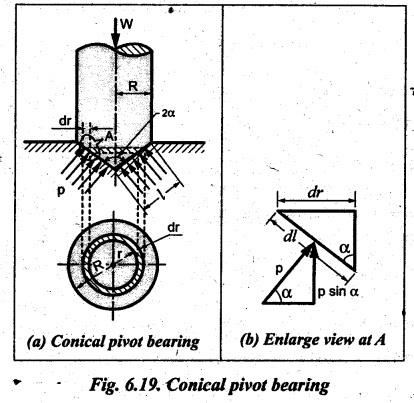
1. Considering Uniform Pressure Theory
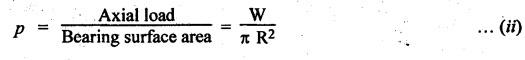

2. Considering Uniform Wear Theory
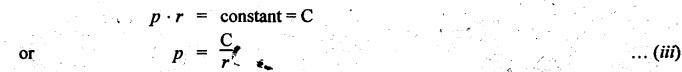

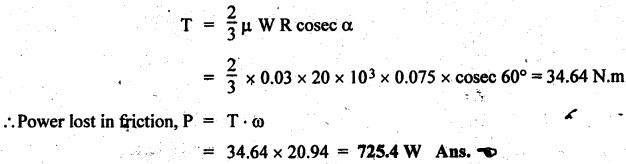
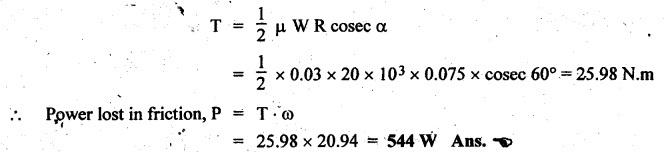

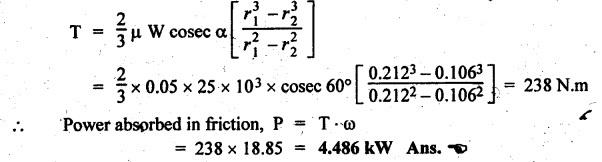
Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - conical pivot bearing
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
