Theory of Machines: Unit III: Friction in Machine Elements
condition for maximum power transmission
Friction in Machine Elements - Theory of Machines
For maximum power, differentiate the above expression with respect to v and equate to zero.
CONDITION FOR MAXIMUM POWER TRANSMISSION Power transmitted by a belt is given by For maximum power, differentiate the above expression with respect to v and equate to zero. Hence, the power transmitted shall be maximum when the centrifugal tensión (TC) is one third of the maximum belt tension (Tmax). Example 8.8 A 100 mm wide and 10 mm thick belt transmits 5 kW between two parallel shafts. The distance between the shaft centres is 1.5 m and the diameter of the smaller pulley is 440 mm. The driving and the driven shafts rotate at 60 rpm and 150 rpm respectively. Find the stress in the belt if the two pulleys are connected by (i) an open belt, and (ii) a cross belt. The coefficient of friction is 0.22. [A.U., Nov/Dec 2010] Given data: b = 100 mm 0.1 m; t = 10 mm = 0.01 m; P = 5 kW = 5000 W; x = 1.5 m; d2 = 440 mm = 44 m; N1 = 60 rpm; N2 = 150 rpm; μ = 0.22. Solution: (i) Stress in the belt for an open belt drive: We know that power transmitted, On solving equations (i) and (ii), we get T2 = 1521.25 N, and T1 = 2968 N We know that maximum tension in the belt (ii) Stress in the belt for a cross belt drive: On solving equations (ii) and (iii), we get T2 = 1042.04 N, and T1 = 2488.40 N Example 8.9 A leather belt is required to transmit 7.5 kW from a pulley 1.2 m in diameter, running at 250 rpm. The angle embraced is 165° and the coefficient of friction between the belt and the pulley is 0.3. If the safe working stress for the leather belt is 1.5 MPa, density of leather 1 Mg/m3 and thickness of belt 10 mm, determine the width of the belt taking centrifugal tension into account. Given data: Solution: Let b = Width of the belt in metres We know that velocity of the belt, On solving equations (i) and (ii), we get T1 = 825.2 N and T2 = 347.75 N We know that mass of the belt per metre length, Example 8.10 A pulley is driven by a flat belt, angle of lap being 120°. The belt weighs 6 N per meter run. The coefficient of friction is 0.3 and maximum stress in the belt is not to exceed 2 MPa. The belt is 100 mm wide and 6 mm thick. Find the maximum power that can be transmitted and the corresponding speed of the belt. Given data:_ θ = 120° = 120° × (π/180°) = 2.09 rad; w = 6 N/m or m = 6/9.81 = 0.612 kg/m; μ = 0.3; σ = 2 MPa = 2 × 106 N/m2; b = 100 mm = 0.1 m; t = 6 mm = 0.006 m Solution: Speed of the belt for maximum power: We know that maximum tension, Tmax = σ • b • t = 2 × 106 × 0.1 × 0.006 = 1200 N and mass of the belt per metre length, m = 0.612 kg/m (given) ⸫ Speed of the belt for maximum power, Maximum power transmitted: We know that for maximum power to be transmitted, centrifugal tension is given by, and tension in the tight side of the belt, ⸫ Maximum power can be transmitted,


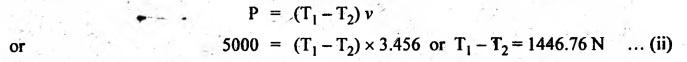










Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - condition for maximum power transmission
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
