Matrices and Calculus: Unit II: Differential Calculus
Concavity
Definition, Theorem, Worked Examples, Exercise with Answers | Differential Calculus
The sign of derivative of a function in an interval says where the graph of ƒ is increasing or decreasing, but it does not reveal the direction of bending of the curve.
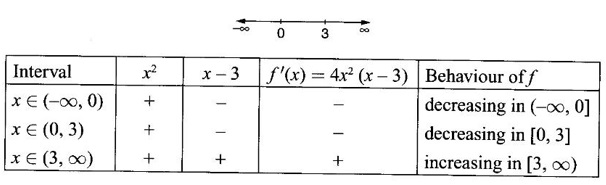
CONCAVITY The sign of derivative of a function in an interval says where the graph of ƒ is increasing or decreasing, but it does not reveal the direction of bending of the curve. This aspect of the shape of the curve is called concavity. Definition 2.25 Let ƒ be a differentiable function in the interval (a, b). The graph of ƒ, namely the curve given by y = f(x) is said to be concave up in (a, b) if the curve lies above every tangent to the curve in the interval (a, b). The curve is concave down in (a, b) if the curve lies below every tangent to the curve in (a, b) Concave down is sometimes referred as convex up Theorem 2.12 Criterion for Concavity Let f be defined in [a, b] and twice differentiable in (a, b). Then (i) The graph of ƒ is concave down in (a, b) if ƒ"(x) < 0 ∀ x ∈ (a, b) (ii) The graph of ƒ is concave up in (a, b) if ƒ"(x) > 0 ∀ x ∈ (a, b) Example 1 Show that the curve y = x3 is concave up in (0, ∞) and concave down in (-∞, 0) Solution Given y = x3, in (-∞, ∞) ⸫ the curve is concave up in (0, ∞) and concave down in (−∞, 0). Tangent at the origin is the x-axis. Notice that at the point O, the curve changes from concave down to concave up. It is a special point called point of inflection. A point P on the curve y = f(x) of a continuous function ƒ is called a point of inflection if the curve changes from concave up to concave down at P and vice versa. Criteria for point of inflection: 1. If the function ƒ is such that f"(c) = 0 and ƒ'" (c) ≠ 0, then the point (c, f(c)) is a point of inflection on the curve y = f(x). 2. If the function f is such that ƒ"(x) changes sign in a neighbourhood (c -δ, c + δ) of c as x increases in the neighbourhood, then the point (c, f(c)) is a point of inflection on the curve (even if ƒ"(c) = 0 or ƒ"(c) does not exist). Example 1 Test the concavity of the curve y = loge x Solution: Given y = loge x, x > 0 ⸫ the curve is concave down in (0, ∞) Example 2 Find the intervals in which the curve y = x2 - 6x3 + 12x2 + 4x + 10 is concave up or down. Also find the points of inflection. Solution We find x = 1 and x = 2 are points where the curve changes shape. Hence at x = 1, x = 2, the curve has points of inflection When x = 1, y = 21 and when x = 2, y = 34 ⸫ the points (1, 21), (2, 34) are points of inflection on the curve. Example 3 Sketch the graph of the function f(x) = x4 − 4x3 + 10 using the informations of 1. extrema 2. Increasing or decreasing 3. concavity 4. Points of inflection Solution Given f(x) = x4 − 4x3 + 10, x ∈ (−∞, ∞) ⸫ ƒ'(x) = 4x3 – 12x2, ƒ"(x) = 12x2 - 24x ⇒ f'(x) = 0 ⇒ 4x3 – 12x2 = 0 ⇒ 4x2 (x – 3) = 0 x = 0 or 3 The critical points x = 0 and x = 3 divide the domain (-∞, ∞) into non overlapping intervals (-∞, 0), (0, 3), (3, 0) in which f'(x) is either positive or negative In a neighbourhood of x = 0, there is no change of sign of f'(x) ⸫ x = 0 is neither a maximum nor a minimum. In a neighbourhood of x = 3, f(x) changes from negative to positive and so it is a local minimum and minimum value = 34 - 4⸱33 + 10 = -17. For concavity In the neighbourhood of x = 0, f"(x) changes sign and so at x = 0 there is a point of inflection on the curve. In the neighbourhood of x = 2, f"(x) changes sign and so there is a point of inflection. When x = 0, ƒ(0) = 10 and when x = 2, f(2) = -6 ⸫ the points of inflection on the curve are (0, 10), (2, −6) Summary: Combine the 2 tables Example 4 Find the points of inflection, if any, for f(x) = x4 Solution Given f(x) = x4 Domain is (-∞, ∞) ⸫ f'(x) = 4x3 and ƒ "(x) = 12x2 > 0 ∀x ≠ 0 ⸫ f is concave up in (-∞, 0) and (0, ∞) In a neighbourhood if x = 0, f"(x) does not change sign. So, x = 0 is not a point of inflection. Hence there is no point of inflection on this curve. Example 5 For the function f(x) = 2 + 2x2 – x4, find the intervals of increase or decrease, local maximum and minimum values, the intervals of concavity and the inflexion points. Solution Given f(x) = 2 + 2x2 – x4 ⸫ ƒ'(x) = 4x − 4x3 To find the critical points solve f'(x) = 0 The critical points x = -1, 0, 1 divide the domain of the function (-∞, ∞) into subintervals (-∞, −1), (-1, 0), (0, 1), (1, ∞) where the derivative is either positive or negative and hence f(x) is either increasing or decreasing f'(x) = 4x - 4x3 = - 4x (x2 - 1) = − 4x (x + 1) (x − 1) To find maxima and minima, we use second derivative test. We have ƒ'(x) = 4x − 4x3 ⸫ f"(x) = 4 - 12x2 When x = -1, ƒ"(-1) = 4 – 12(−1)2 = −8 < 0 ⸫ f(x) is maximum at x = -1 and the maximum value is f(-1) = 2 + 2 (-1)2 - (−1)4 = 2 + 2 - 1 = 3 When x = 0, ƒ"(0) = 4 - 0 = 4 > 0 ⸫ f(x) is minimum when x = 0 and the minimum value is f(0) = 2 When x = 1,ƒ"(1) = 4 - 12 ⸱12 = -8 < 0 ⸫ f(x) is maximum when x = 1 and the maximum value is f(1) = 2 + 2 – 1 = 3 To find Concavity: f"(x) = 4 - 12x2 Example 6 For the function f(x) = 2x3 + 3x2 - 36x + 5, find (i) Where the function is increasing or decreasing (ii) The local maxima and minima using first derivative test (iii) The intervals of concavity. (iv) Points of inflexion Solution Given f(x) = 2x3 + 3x2 - 36x + 5 f'(x) = 6x2 + 6x - 36 = 6(x2 + x - 6) = 6(x + 3) (x − 2) To find the critical points solve ƒ'(x) = 0 ⇒ 6(x + 3)(x - 2) = 0 ⇒ x = -3, 2 (i) The critical points divide the domain (-∞, ∞) into intervals (-∞, -3), (-3, 2), (2, ∞) in which f'(x) is either positive or negative and hence increasing or decreasing. 1. Find the intervals of monotocity of f (x) = 2x2 - ln x 2. If Prove that f is increasing in 3. Using the function 4. Find the intervals in which the curve y = 3x5 - 40x3 + 3x -20 is concave up or down. 5. Show that 6. For the function f(x) = x4 - 8x3 + 22x2 - 24x + 3 find (i) The intervals in which f(x) is increasing or decreasing (ii) Point of local maxima and minima (iii) The subintervals in which f(x) is concave up or down (iv) Points of inflexion, if any 7. For the function f(x) = x3 - 12x + 5, find (i) The intervals of increasing and decreasing nature. (ii) maxima and minima 8. For the function y = -2x3 + 6x2 - 3, find (i) The local maxima and minima (ii) Points of inflexion, if any 9. For the function f(x) = (x - 2)3 + 3, find (i) maxima and minima (ii) points of inflexion 1. Decreasing in 3. eπ is bigger 4. Concave down in (-∞, -2) and (0, 2) Concave Up in (-2, 0) and (2, ∞) 6. Decreasing in (-∞, 1) and (2, 3) Increasing in (1, 2) and (3, ∞) min at x = 1 and 3 max at x = 2 7. Increasing in (-∞, −2), (2, 0) Decreasing in (−2, 2) Maximum at x = -2, Maximum value = 21 Minimum at x = 2, Minimum value = -11 8. Maximum when x = 2, maximum value = 5 Minimum when x = 0, Minimum value = −3 Point of inflexion at x = 1 9. Either maximum or minimum point of inflexion at x = 2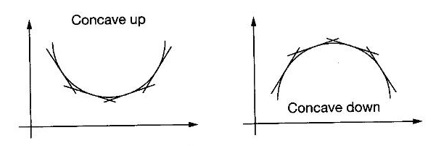
WORKED EXAMPLES
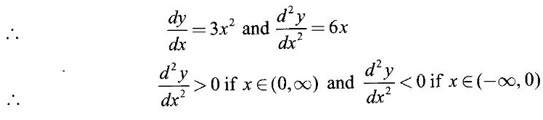

Definition: Point of inflection
WORKED EXAMPLES
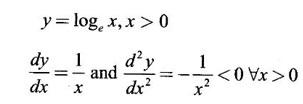







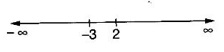

EXERCISE 2.12
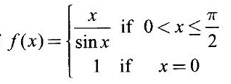

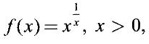 determine the bigger of the two numbers πe and eπ
determine the bigger of the two numbers πe and eπ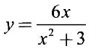 has three points of inflection and they are collinear.
has three points of inflection and they are collinear.ANSWERS TO EXERCISE 2.12
 and increasing in
and increasing in 

Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Theorem, Worked Examples, Exercise with Answers | Differential Calculus - Concavity
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
