Engineering Physics: Unit IV: Basic Quantum Mechanics
Compton Effect
Definition, Statement, Explanation, Theory, Equation, Experimental verification, Physical significance, Derivation
Compton effect refers to the change in the wavelength of scattered X-rays by a material
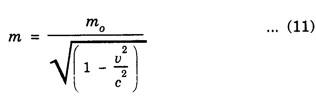
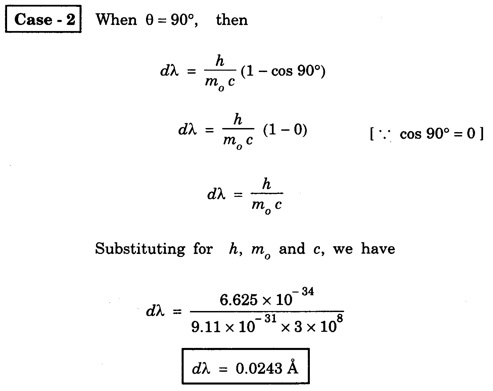
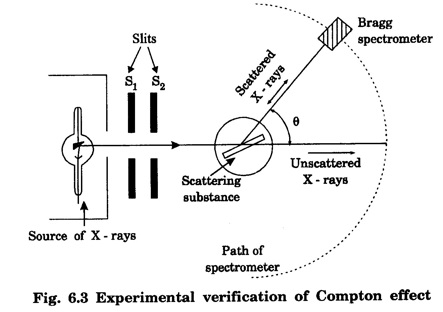
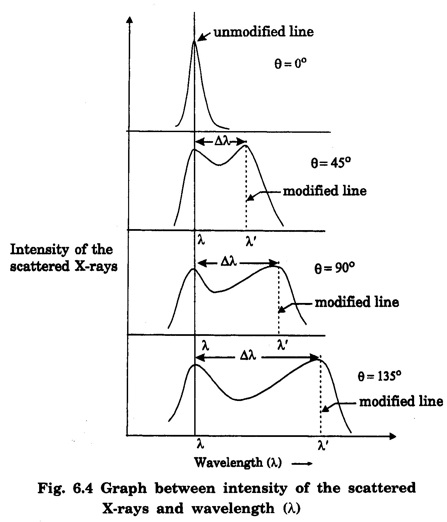
COMPTON EFFECT Compton effect refers to the change in the wavelength of scattered X-rays by a material. Statement When a beam of X -rays is scattered by a substance of low atomic number, the scattered X-ray radiation consists of two components. One component has the same wavelength λ as the incident ray and the other component has a slightly longer wavelength λ. The change in the wavelength of scattered X- rays is known as Compton shift. The phenomenon is called Compton effect. The radiations of unchanged wavelength in the scattered radiations are called unmodified radiations. The radiations of longer wavelength are known as modified radiations. The change of wavelength is due to loss of energy of the incident X -rays. The compton effect was explained on the basis of quantum theory of radiation. The X - radiation consists of quanta or photons each having an energy of hv. These photons move with velocity of light (c). They obey the laws of conservation of energy and momentum when they undergo collision The whole process is treated as a particle - particle collision between X - ray photon and a loosely bound electron of the atom in the scattering substance. When a photon of energy hv collides with a free electron of the scattering substance, which is assumed to be at rest initially, the photon transfers some of its energy to the electron (Fig. 6.1). The electron gains kinetic energy and it recoils with velocity v. Therefore, the scattered photon has lower energy, (lower frequency and longer wavelength) than that of the incident one. Consider an X -ray photon striking an electron at rest (Fig 6.2 a). This X -ray photon is scattered through an angle θ to X-axis from its initial direction of motion (Fig. 6.2 b). Let the frequency of scattered photon be v' and its energy hv'. During the collision, X - ray photon gives a fraction of its energy to the free electron. This free electron of mass m gains energy and it moves with a velocity v at an angle ϕ to X-axis. Energy of incident photon = hv Energy of electron at rest = m0c2 where m0 - rest mass of the electron, c - velocity of light. Total energy before collision = hv + m0c2 Energy of scattered photon = hv' Energy of scattered electron = mc2 where m is the mass of electron. when it moves with velocity v. Total energy after collision = hv' + mc2 Applying the law of conservation of energy, i.e., Total energy before collision = Total energy after collision Total momentum along X-axis Before collision Momentum of photon along X-axis = hv/c Momentum of electron along X-axis = 0 Total momentum along X-axis = hv/c After collision Since the momentum is vector quantity, it is resolved along X-axis and Y-axis, then Momentum of photon along X-axis = hv’/c cos θ Momentum of electron along X-axis = mv cos θ Total momentum along X-axis after collision Applying the law of conservation of momentum ie., Total momentum before collision = Total momentum after collision Total momentum along Y-axis Before collision Momentum of photon along Y-axis = 0 Momentum of electron along Y-axis = 0 Total momentum along Y-axis = 0 After collision Momentum of photon along Y - axis = hv’/c sin θ Momentum of electron along Y - axis = - mv sin ϕ [negative sign indicates negative Y - direction] Total momentum along Y - axis = hv’/c sin θ - mv sin ϕ Applying the law of conservation of momentum ie., Total momentum before collision = Total momentum after collision Squaring eqn (3) and eqn (5) and then adding, we get Subtracting eqn (7) from eqn (9), we get From the theory of relativity, the variation of mass with velocity is given by Squaring the eqn (11) on both sides, we have Multiplying c2 on both sides, we have Substituting eqn (12) in eqn (10), we get Multiplying c on both sides of eqn (13), we have Therefore, the change in wavelength is given by It is found that the change in wavelength (da) does not depend on the wavelength of the incident radiation and the nature of the scattering substance. But it depends only on the angle of scattering (θ). i.e. Along the incident direction, there is no change in wavelength This difference in wavelength is known as Compton wavelength of electron. Thus, the change in wavelength is maximum at θ = 180°. A beam of monochromatic X-rays of wavelength λ is made to incident on a scattering substance (Fig. 6.3). The scattered X-rays are received by Bragg spectrometer. The intensity of scattered X-rays is measured for various scattering angles. The graph is plotted (intensity Vs wavelength) as shown in fig. 6.4. It is found that the curves have two peaks, one corresponding to unmodified radiation and other corresponding to modified radiation. The difference between two peaks on the wavelength axis gives Compton shift. The curves show that the greater the scattering angle, the greater is Compton shift in accordance with the expression. The change in wavelength dλ = 0.0243 Å at θ = 90° is found to be in good agreement with the theoretical value 0.0243 Å. Thus, Compton effect is experimentally verified. The experimental observations were in perfect agreement with the prediction of the above equation, thus holding the Einstein's concept of photon as completely valid. In the compton effect, the compton shift is explained on the basis that the X-ray photons collide with electrons. In the collision, the energy exchange between the two occurs as it is a kind of particle-particle collision. Thus, it demonstrates the particle nature of X-rays which we know are electromagnetic waves, or in other words, it signifies the particle nature of waves in general.Explanation
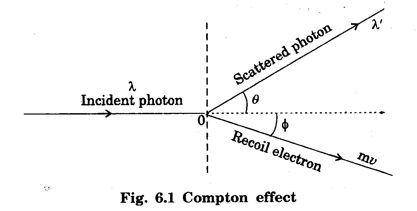
Theory of Compton effect (Derivation)
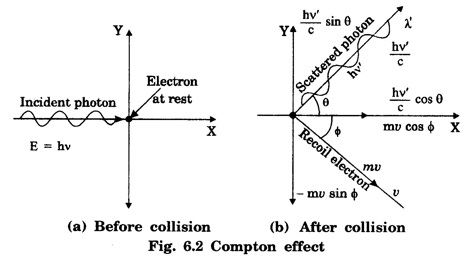
Total energy before collision
Total energy after collision


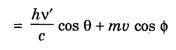
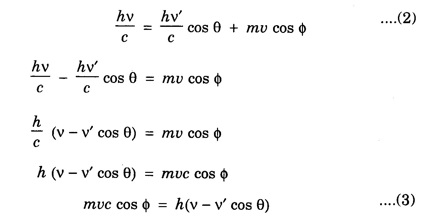
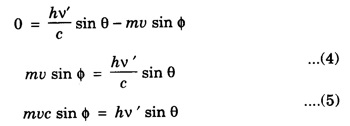

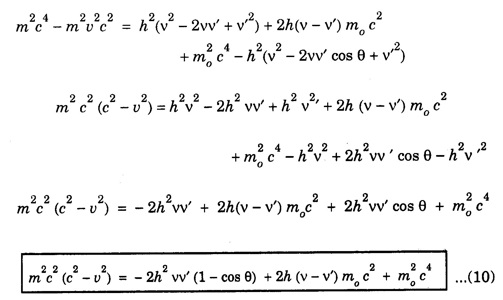
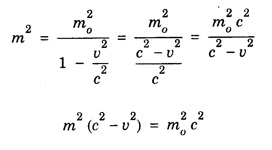
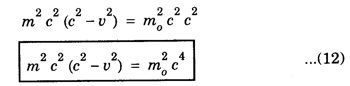
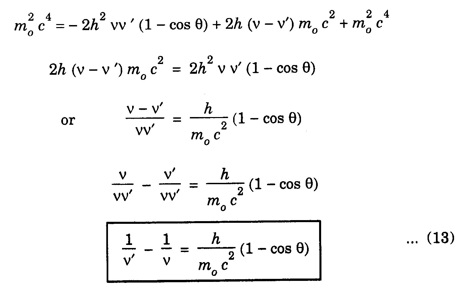


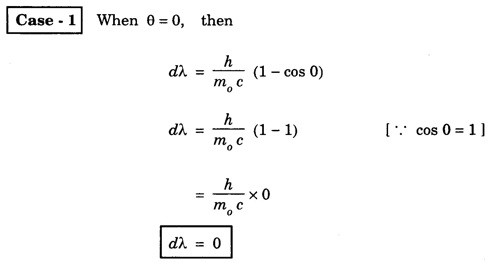

Experimental verification of Compton effect
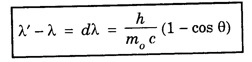
Physical significance of compton effect
Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : Definition, Statement, Explanation, Theory, Equation, Experimental verification, Physical significance, Derivation - Compton Effect
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
