Matrices and Calculus: Unit II: Differential Calculus
Chain Rule or Derivative of Composite Function
Worked Examples, Exercise problems with Answers | Differential Calculus
Worked Examples, Exercise with Answers: Chain Rule or Derivative of Composite Function: Matrices and Calculus: Differential Calculus
CHAIN RULE OR DERIVATIVE OF COMPOSITE FUNCTION
If y = f(u) and u = g(x), where f and g are differentiable, then the derivative of the composite functions is (f ◦ g)'(x) = ƒ'(g(x)) · g'(x)
In Leibnitz notation 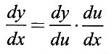
The chain rule can be extended due to the composition of more than two functions. If y = f(u), u = g(x), x = h(t), where f, g, h are differentiable functions.
Then y is a function of t.

In Leibnitz notation
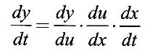
WORKED EXAMPLES
Example 1
Differentiate cos(x3 + 2x2 + 1) w. r. to x
Solution
Let y = cos(x3 + 2x2 + 1) (1)

Example 2
Find 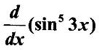
Solution
Let y = sin5 3x

Example 3
Find 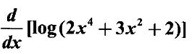
Solution
Let y = log(2x2 + 3x2 + 2)

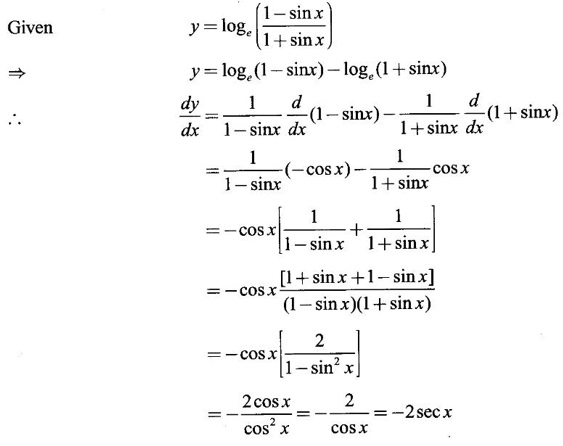
Example 4
If y = 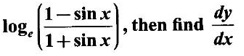
Solution
Example 5
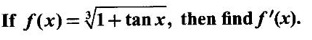
Solution

Example 6
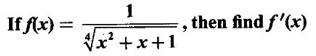
Solution
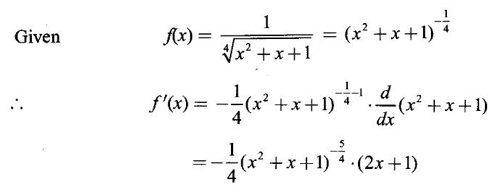
Example 7

Solution

Example 8

Solution

Instead of substitution we do it directly.
Example 9
If f(x) = sin[cos(tan x)], then find f'(x)
Solution
Given f(x) = sin[cos(tan x)]
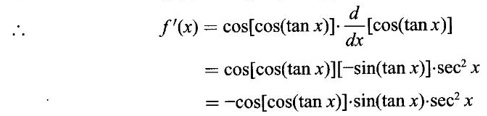
Example 10
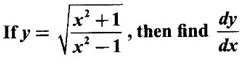
Solution

Example 11
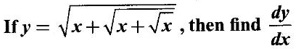
Solution
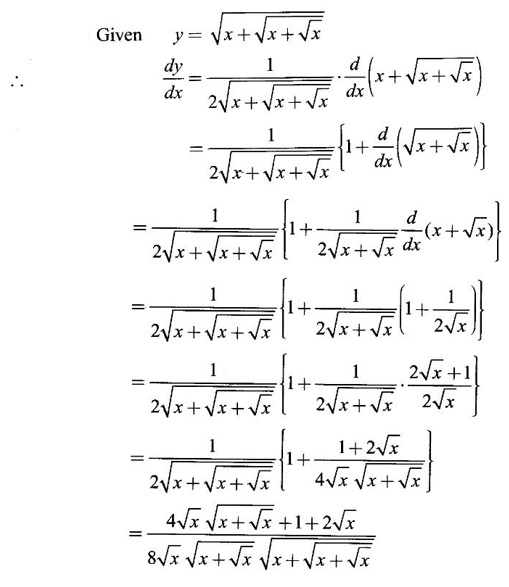
Example 12
If f(x) = sin(cos2 x) cos(sin2 x), then find ƒ'(x)
Solution
Given f(x) = sin(cos2 x) cos(sin2 x)
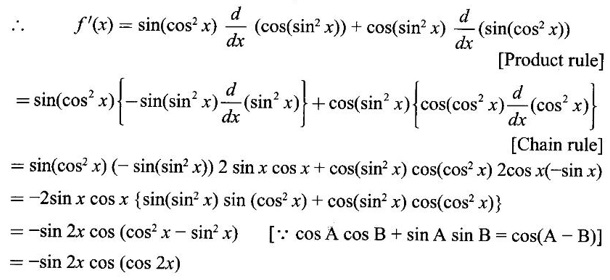
Example 13

Solution

Example 14
If F(x) = f(xf(x f(x)))
where f(1) = 2, ƒ(2) = 3, ƒ'(1) = 4, ƒ'(2) = 5, ƒ'(3) = 6. Find F'(1).
Solution
Given F(x) = F(x) = f[xf(x f(x))], f(1) = 2, ƒ(2) = 3, ƒ'(1) = 4, ƒ'(2) = 5, ƒ'(3) = 6.

Put x = 1 then

=ƒ'[3][4.5+ 2.5 + 3] = 6[33] = 198
EXERCISE 2.6
Differentiate the following functions

ANSWERS TO EXERCISE 2.6

Matrices and Calculus: Unit II: Differential Calculus : Tag: : Worked Examples, Exercise problems with Answers | Differential Calculus - Chain Rule or Derivative of Composite Function
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
