Engineering Physics: Unit I: Mechanics
Centre of mass (cm) of continuous bodies (rigid bodies)
The centre of masses of homogeneous and regular shaped bodies coincides with their geometrical centre.
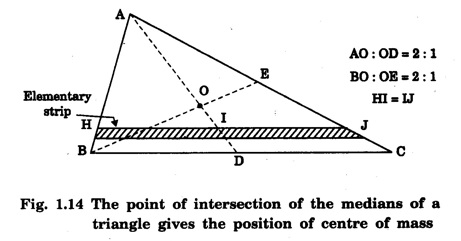
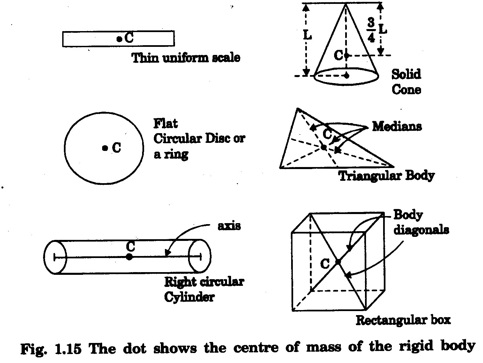
CENTRE OF MASS (CM) OF CONTINUOUS BODIES (RIGID BODIES) Experimental location of the centre of mass The centre of masses of homogeneous and regular shaped bodies coincides with their geometrical centre. Hence it can be easily located; but if the body is of irregular shape the location of its centre of mass is difficult. However, since the centre of mass is found to coincide with centre of gravity of the bodies, it can be easily obtained either by pivoting the body to a balanced position or suspending it from some fixed point in it. Basically, both are similar methods. As an illustration, we describe below the method of suspension to locate the centre of mass of any regular or irregular shaped body. The body is first hung from some (any) point P and a vertical line PQ is drawn when the body is in equilibrium. The body is then hung from some other point R and a vertical line RS is drawn (Fig 1.12). The point of intersection C of these two lines PQ and RS gives the position of centre of mass. Fig. 1.13 shows a right circular solid cone of base radius a and height h. Let ρ be the density of the material of the cone. If the solid cone is homogeneous, then its mass The centre of mass lies on the axis of symmetry AO. The cone is considered to be made up of large number of circular discs, each of thickness dy. Let us consider one such elementary disc of radius x at a distance y from the vertex A of the solid cone. The mass of this elementary disc is dm = ρ (π x2) dy ... (1) From the figure 1.13, Now from equation (1), we have for the distance of centre of mass on the axis of symmetry AO as measured from the vertex A as On substituting the value of dm, we get where the limits of y is taken from y = 0 to y = h to cover the entire solid cone filled with such elementary discs. It gives The CM of cone from its vertex YCM is written as RCM: The medians of the triangle are axes of symmetry in the base of triangular sheets. We simply draw any two medians of the triangle which intersect at a point. This point is the centre of mass of the triangular body (Fig. 1.14). We know that the medians bisect each other in the ratio of 2:1 the position of centre of mass on any medians is obtained by dividing that median in the ratio 2:1 the larger portion being towards the vertex. That point is the centre of mass. However, the position of centre of mass can also be calculated by assuming the triangle to be made up of large number of strips parallel to one side of the triangle and placed one above the other as shown in the fig. 1.14. Fig 1.15. shows the centre of masses of some regular shaped homogeneous rigid bodies. • For a rigid body, the centre of mass is a point at a fixed position with respect to the body as a whole. Depending on the shape of the body and the way the mass is distributed in it, the centre of mass is a point that may or may not be within the body. • If the shape is symmetrical and the mass distribution is uniform, we can usually find the location of the centre of mass quite easily. • For a long thin rod of uniform cross section and density, the centre of mass is at the geometrical centre. • For a thin circular plane ring, it is again at the geometrical centre of the circle. • For a flat circular disc or rectangle, again the centre of mass is at the geometrical centre. Generally, the centre of mass coincides with the centre of gravity of regularly shaped bodies. In case of rigid body, the internal forces are taken as zero and only the external forces acting on the body are considered. Note Difference between centre of gravity and centre of mass • The centre of gravity of a body is a point where the whole weight of the body supposed to be concentrated. • The centre of mass of a body is that point, where the whole mass of the body is supposed to be concentrated. For uniform geometrically shaped, bodies the centre of gravity coincides with centre of mass. However, they do not coincide in bodies whose density is not uniform throughout.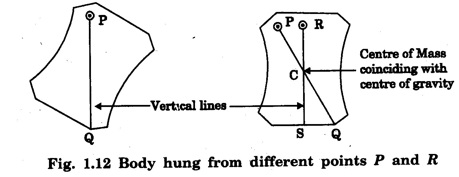
Centre of mass of a solid cone
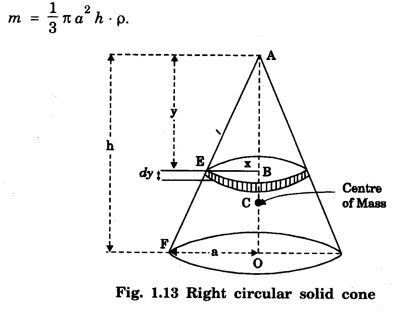


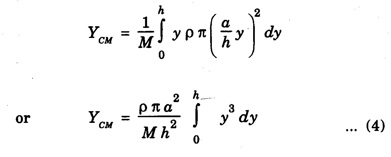
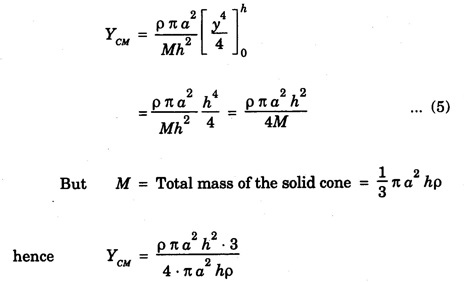
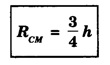 Thus, CM of a solid cone is at a distance of 3/4 h from vertex of the cone along its axis.
Thus, CM of a solid cone is at a distance of 3/4 h from vertex of the cone along its axis.Centre of mass of a triangular lamina
Centre of mass of some regular objects
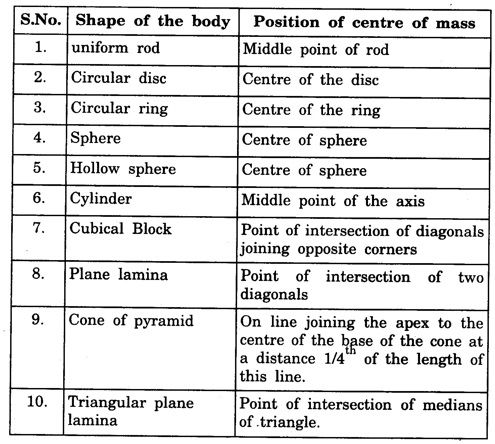
Engineering Physics: Unit I: Mechanics : Tag: : - Centre of mass (cm) of continuous bodies (rigid bodies)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
