Engineering Physics: Unit I: Mechanics
Centre of Mass (CM) and Motion of CM
Definition, Examples, Equations
A point in the system at which whole mass of the body is supposed to be concentrated is called centre of mass of the body.
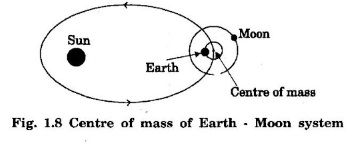
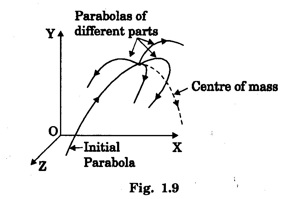
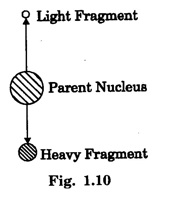
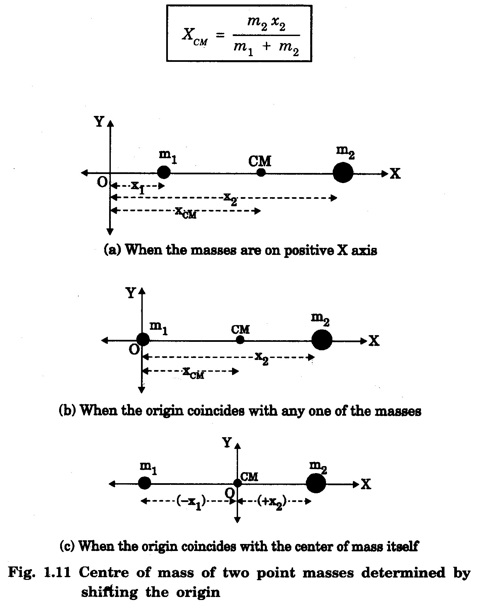
CENTRE OF MASS (CM) Every system or body is a collection of large number of tiny particles. In translatory motion of a body, every particle experiences equal displacement with time. Therefore, the motion of the whole body may be represented by a particle. But when the body rotates or vibrates during translatory motion, then its motion can be represented by a point that moves in the same way as that of a single particle subjected to the same external forces would move. This point is called centre of mass of a system. Definition A point in the system at which whole mass of the body is supposed to be concentrated is called centre of mass of the body. Therefore, if a system contains two or more particles, its translatory motion can be described by the motion of the centre of mass of the system. (i) Motion of planets and its satellite • Let us consider the motion of the centre of mass of the Earth and moon system (Fig 1.8). The moon moves round the Earth in a circular orbit and the Earth moves round the sun in an elliptical orbit. It is more correct to say that the Earth and the moon both move in circular orbits about their common centre of mass in an elliptical orbit round the Sun. For the system consisting of the Earth and the moon, their mutual gravitational attractions are the internal forces. The gravitational attraction by the Sun attraction on both the Earth and moon are the external forces acting on the centre of mass of the system. (ii) Projectile Trajectory • When a cracker is fired at an angle with the horizontal and when it explodes in the air, then different pieces of the cracker follows different parabolic paths. The centre of mass of all the pieces of the cracker continue to move in the initial parabolic path as shown by a dotted line in fig. 1.9. This is because the different pieces of the cracker move under the effect of internal forces only. (iii) Decay of a Nucleus • Let us consider a spontaneous decay of a radioactive nucleus into two fragments as shown in fig. 1.10. The two fragments move apart in opposite directions obeying the laws of conservations of energy and momentum. Since the parent nucleus is at rest, therefore, the centre of mass of the system remains at rest. The nucleus decays under the effect of internal forces. The heavier fragment moves with less speed while the lighter fragment moves with high speed. With the equations for centre of mass, let us find the centre of mass of two point masses m1 and m2, which are at positions x1 and x2 respectively on the X-axis. For this case, we can express the position of centre of mass in the following three ways based on the choice of the co-ordinate system. (i) When the masses are on positive X-axis The origin is taken arbitrarily so that the masses m1 and m2 are at positions x1 and x2 on the positive X-axis as shown in figure 1.11 (a). The centre of mass is on the positive X-axis at XCM and it is given by the equation, (ii) When the origin coincides with any one of the masses The calculation is minimised if the origin of the coordinate system is made to coincide with any one of the masses as shown in figure 1.11(b). When the origin coincides with the point mass m1, its position x1 is zero, (i.e. x1 = 0). Then, The equation further is simplified as, (iii) When the origin coincides with the centre of mass itself If the origin of the coordinate system is made to coincide with the centre of mass then, XCM = 0 and the mass m1 is found to be on the negative X-axis as shown in fig. 1.11(c). Hence, its position x1 is negative, (i.e., - x1). The equation given above is known as principle of moments. MOTION OF CENTRE OF MASS When a rigid body moves, it centre of mass will also move along the body. For kinematic quantities like velocity For simplicity, let us take the motion along X direction only. In the absence of external force, This does not affect the position of the centre of mass. This mean that the centre of mass is in a state of rest or uniform motion. Hence, From equations (1) and (2), Here, the individual particles may still move with their respective velocities and accelerations due to internal forces. In the presence of external force, (i.e. Examples for motion of centre of mass
Centre of mass of two point masses
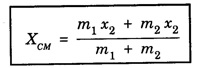
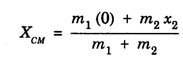
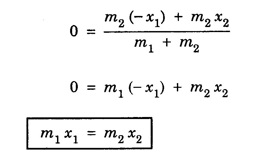
![]() and acceleration
and acceleration ![]() of the centre of mass, we can differentiate the expression for position of centre of mass with respect to time once and twice respectively.
of the centre of mass, we can differentiate the expression for position of centre of mass with respect to time once and twice respectively.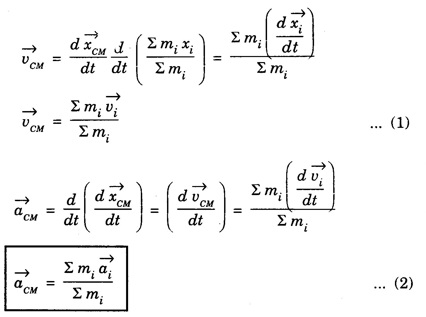
![]() = 0, the individual rigid bodies of a system can move or shift only due to the internal forces.
= 0, the individual rigid bodies of a system can move or shift only due to the internal forces.![]() is zero when centre of mass is at rest or has uniform motion (
is zero when centre of mass is at rest or has uniform motion (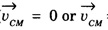 = constant). There is no acceleration of centre of mass,
= constant). There is no acceleration of centre of mass, 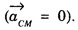
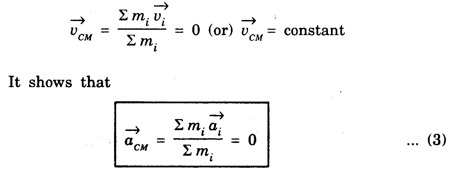
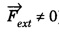 ), the centre of mass of the system will accelerate as given by the following equation.
), the centre of mass of the system will accelerate as given by the following equation.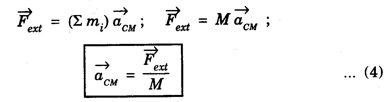
Engineering Physics: Unit I: Mechanics : Tag: : Definition, Examples, Equations - Centre of Mass (CM) and Motion of CM
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
