Matrices and Calculus: Unit I: Matrices
Cayley-Hamilton Theorem
Worked Example Problems
Every square matrix satisfies its characteristic equation
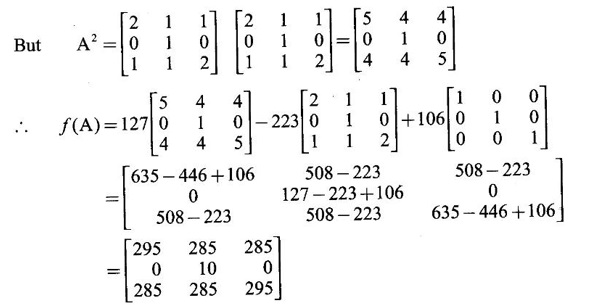
CAYLEY-HAMILTON THEOREM Theorem 1.3.1 Every square matrix satisfies its characteristic equation Cayley-Hamilton theorem has two important uses (1) to find the inverse of a non-singular matrix A and (2) to find higher integral powers of A. WORKED EXAMPLE Example 1 Verify that A= Solution Given A = The characteristic equation of A is |A - λI| = 0 ⇒ λ2 − S1λ + S2 = 0 where S1 = 1 + (-1) = 0, S2 = |A| = -1 - 4 = -5 ⸫ the characteristic equation is λ2 - 5 = 0 (1) By Cayley-Hamilton theorem, A satisfies (1) i.e. A2 – 5I = 0 (2) We shall now verify this by direct computation. ⇒ A2 – 5I = 0 Hence A satisfies its characteristic equation. To find A4: We have A2 = 5I [from (2)] Example 2 Verify Cayley-Hamilton theorem for the matrix A = Solution Given A = The characteristic equation of A is |A - λI| = 0 ⇒ λ2 − S1λ + S2 = 0 where S1 = 1 + 3 = 4, S2 = |A| = 3 – 8 = -5 ⸫ the characteristic equation is λ2 - 4λ - 5 = 0 (1) 50 By Cayley-Hamilton theorem, A satisfies (1) ⸫ A2- 4A - 5I = 0 (2) We shall now verify this by direct computations. ⇒ A2 - 4A - 51 = 0. Hence the theorem is verified. To find A-1: We have 5I = A2 - 4A Multiply by A-1, we get 5A-1 = A-1A2 - 4A-1 A = A – 4I Finally, to find A5 - 4A4 -7A3 + 11A2 - A – 10I: Consider the polynomial λ5 - 4 λ4 - 7 λ3 + 11 λ2 - λ - 10 Divide it by λ2 - 4 λ - 5. We get the quotient λ3 - 2 λ + 3 and remainder λ + 5 ⸫ λ5 - 4 λ4 - 7 λ3 + 11 λ2 - λ - 10 = (λ2 - 4 λ — 5)( λ3 - 2 λ + 3) + λ + 5 Replace λ by A, we get A5 - 4 A4 - 7 A3 + 11 A2 - A – 10I = (A2 - 4 A — 5I)( A3 - 2 A + 3) + A + 5I = 0 + A + 5I [using (2)] = A + 5I, which is a linear polynomial in A. Example 3 Find the characteristic equation of the matrix A given Solution where S1 = sum of the diagonal elements of A = 2 + 2 + 2 = 6 S2 = sum of minors of the diagonal elements of A = 4 - 1 + 4 - 1 + 4 - 1 = 9 S3 = |A| = 2(4 − 1) + (−2 + 1) + (1 − 2) = 6 – 1 – 1 = 4 ⸫ the characteristic equation is λ3 − 6λ2 + 9λ − 4 = 0 By Cayley-Hamilton theorem, A satisfies its characteristic equation Example 4 Use Cayley-Hamilton theorem to find the matrix A8 - 5A7 + 7A6 - 3A5 + 8A4 - 3A5 + 8A4 - 5A3+ 8A2 – 2A + I if the matrix Solution The characteristic equation is |A –λI| = 0 ⸫ the characteristic equation is λ3 — 5λ2 + 7λ − 3 = 0 By Cayley-Hamilton theorem, we get A3 - 5A2 + 7A – 3I = 0 (1) We have to find the matrix A8 — 5A2 + 7A6 – 3A5 + 8A4 - 5A3 + 8A2 - 2A + I = ƒ(A), say We shall rewrite this matrix polynomial in terms of A3 - 5A2 + 7A – 3I ⸫ the polynomial ƒ(A) = A5(A3 - 5A2 + 7A – 3I) + 8A4 - 5A3 + 8A2 − 2A + I = 8A4 - 5A3 + 8A2 - 2A+ I [Using (1)] = 8A(A3 - 5A2 + 7A – 3I) + 35A3 - 48A2 + 22A + I = 35A3 - 48A2 + 22A + I [Using (1)] = 35(A3 - 5A2 + 7A – 3I) + 127A2 – 223A + 106I = 127A2 - 223A + 106I [Using (1)] Example 5 Verify Cayley-Hamilton theorem and find the inverse of Solution The characteristic equation of A is │A - λI│ = 0 ⸫ the characteristic equation is λ3 - 10 λ2 + 8 λ + 64 = 0 (1) By Cayley-Hamilton theorem A statisfies (1) ⸫ A3 - 10A2 + 8A + 64I = 0 (2) We shall now verify this by direct computations. Now A3 - 10A2 + 8A + 64I ⸫ A3 - 10A2 + 8A + 64I = 0 Hence the theorem is verified. To find A-1: We have 64I = -A3 +10A2 – 8A Multiplying by A-1, we get Example 6 If A = Solution ⸫ the characteristic equation is λ3 - λ2 + λ + 1 = 0 (1) By Cayley-Hamilton theorem A statisfies (1) ⸫ A3 - A2 + A + I = 0 ⇒ A3 - A2 = A - I (2) Multiplying (2) by A, A2, ..., An-3, we get the equations A4 - A3 = A2 - A A5 - A4 = A3 - A2 Adding (2) and all these equations we get = An−4 + 2(A2 –I) (ii) = An-6 + A2 – 1 + 2(A2 –I) = An-6 + 3(A2 –I) (iii) Example 7 If A = Solution Given The characteristic equation is λ2 - 5 = 0 [see example 17] By Cayley-Hamiltons theorem A2 – 5I = 0 (1) To find An, consider the polynomial λn Dividing λn by λ2 – 5 we get λn = (λ2 - 5) φ (λ) + aλ + b (2) where φ (λ) is the quotient and aλ + b is the remainder. We shall now find the values of a and b. Example 8 Using Cayley-Hamilton theorem find A-1, where A = Solution = (1 - 4) + (-7 + 12) + (−7 + 12) = - 3 + 5 + 5 = 7 S3 = |A| = 7(1 - 4) -2(6 - 12) + (-2) (− 12 + 6) = −21 + 12 + 12 = 3 ⸫ the characteristic equation is λ3 − 5 λ2 + 7λ − 3 = 0 By Cayley --Hamilton theorem, A satisfies this equation. ⸫ A3 - 5A2 + 7A – 3I = 0 ⇒ 3I = A3 - 5A2 + 7A Multiply by A-1, 3A-1 = A2 - 5A + 7I Example 9 Verify Cayley-Hamilton theorem for A = Solution = 3 + 28 + 15 = 40 ⸫ The characteristic equation is λ3 + λ2 – 18 λ – 40 = 0. By Cayley-Hamilton theorem A satisfies this equation ⸫ A3 + A2 – 18A – 40I = 0 (1) We shall verify (1) by actual computation. ⸫ A3 + A2 – 18A – 40I = 0. Hence Cayley-Hamilton theorem is verified. We have 40I = A3 + A2 – 18A Multiply by A-1. ⸫ 40A-1 = A2 + A – 18I Example 10 If Solution where S1 = sum of the diagonal elements of A = 3 +5 + 3 = 11 S1 = sum of the minors of diagonal elements of A = 15 -1 + 9 – 1 +15 = 36 = 3 (15 − 1) − (−1)(−3 + 1) + 1.(1 − 5) = 42 - 2 - 4 = 36 ⸫ the characteristic equation is λ3 − 11 λ2 + 36λ – 36 = 0 (1) A satisfies (1) ⸫ A3 – 11A2 + 36A – 36I = 0 (2) We now verify the equation (2) We find A2, A3 Equation (2) is satisfied Hence the Cayley-Hamilton is verified. Row to find A-1 Pneumatic applying (2) A-1, we get Example 11 Using Cayley Hamilton Theorem find A-1 and A4 if A = Solution = 1(3-0) -2(-1 - 0) + (-2) (2 - 0) = 3 + 2 - 4 = 1 The characteristic equation is λ3 − 4 λ2 + 9 λ − 1 = 0 By Cayley Hamilton Theorem, it satisfies the characteristic equation ⸫ A3 - 4А2 + 9A − 1 = 0 Post multiplying by A-1, ⇒ A3A-1 - 4A2A-1 + 9AA-1 - IA-1 = 0 ⇒ A2 - 4A + 9I - A-1 = 0 A-1 = А2 + 4A + 9I and pre multiplying by A, A4 - 4A3 + 9A2 - A = 0 A4 = 4A3 + 9A2 + A EXERCISE Verify Cayley-Hamilton theorem for the following matrices and hence find their inverses. 5. Verify that the matrix A = 6. 7. Find A4 using Cayley-Hamilton theorem for the matrix Find A4 + A3 – 18A2 – 39A + 2I 8. Find the eigen values and eigen vectors of the system of equations 10x1 + 2x2 + x3 = λx1, 2x1 + 10x2 + x3 = λx2, 2x1 + x2 + 10x3 = λx3 [Hint: Equations can be rewritten as (10 - λ)x1 + 2x2 + x3 = 0, 2x1 + (10 − λ)x2 + x3 = 0, 2x1 + x2 + (10 - λ)x3 = 0 9. If λ is an eigen value of a non-singular matrix A, show that |A| / λ is an eigen value of the matrix adj A. [Hint: AX = λ X ⇒ (adj A) (AX) = (adj A) (λX) 10. Verify Cayley-Hamilton theorem for the matrix ANSWERS TO EXERCISE 1.2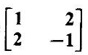 satisfies its own characteristic equation and hence find A4.
satisfies its own characteristic equation and hence find A4.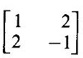
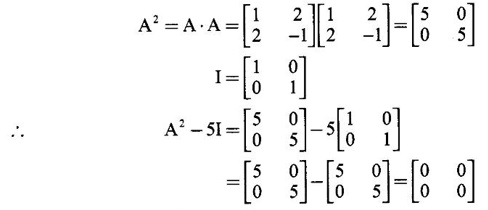
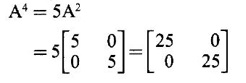
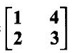 and find its inverse. Also express A5 - 4A4 - 7A3 + 11A2 – A – 10I as a linear polynomial in A.
and find its inverse. Also express A5 - 4A4 - 7A3 + 11A2 – A – 10I as a linear polynomial in A.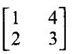
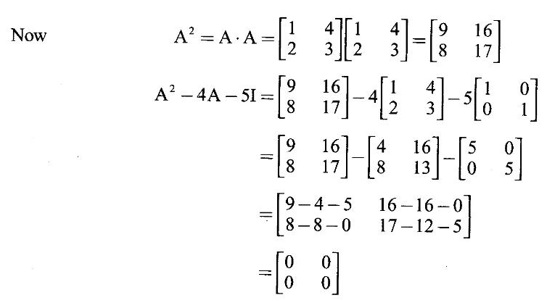
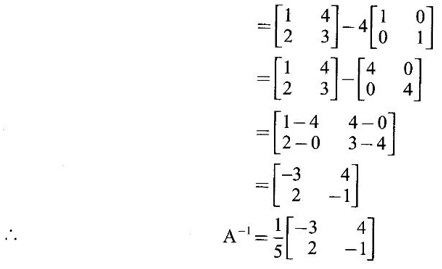
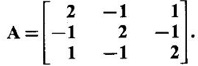 Hence find A-1 and A4.
Hence find A-1 and A4.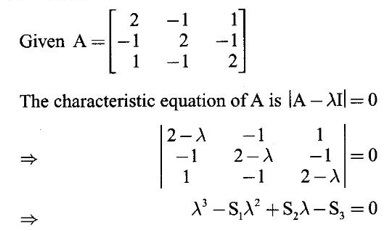
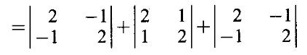

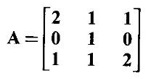
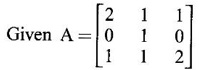
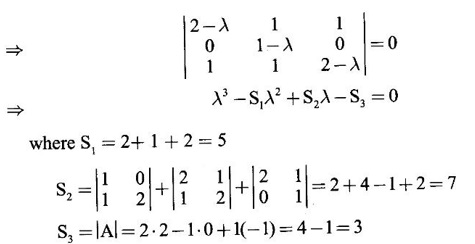


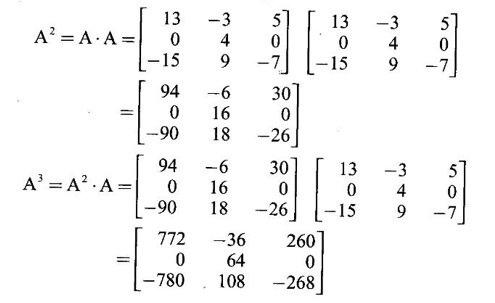


 then show that An = An¬2 + A2 - I for n ≥ 3. Hence find A50.
then show that An = An¬2 + A2 - I for n ≥ 3. Hence find A50.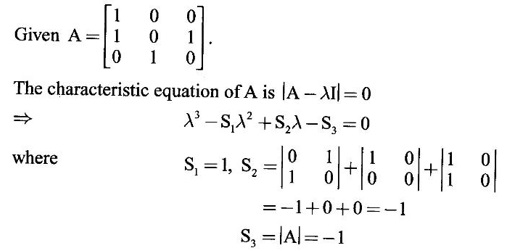
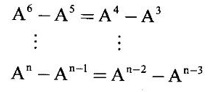


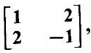 find An in terms of A and I.
find An in terms of A and I.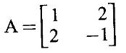

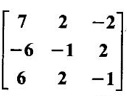
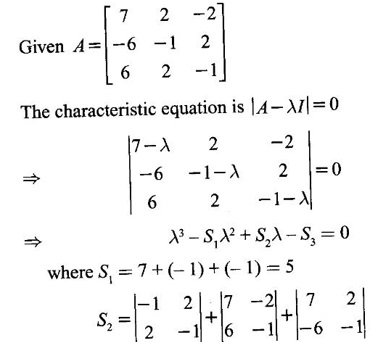
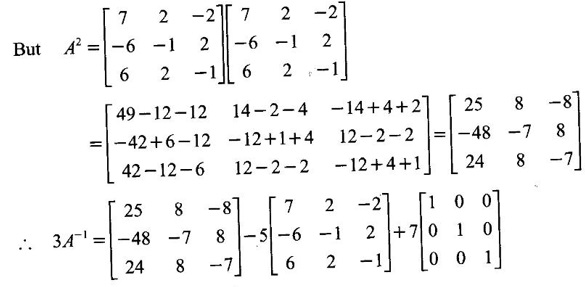
 Hence using it find A-1.
Hence using it find A-1.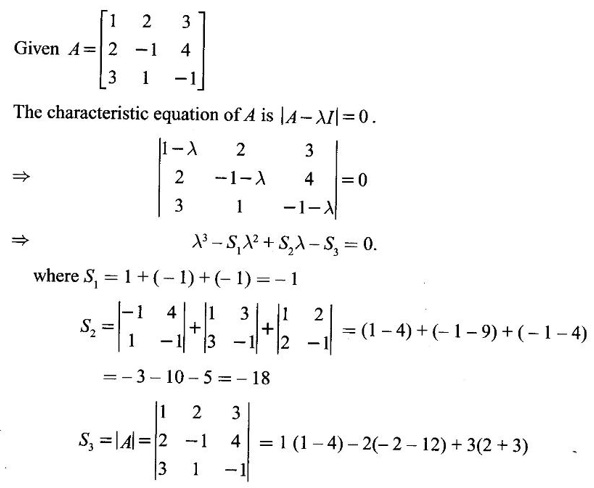

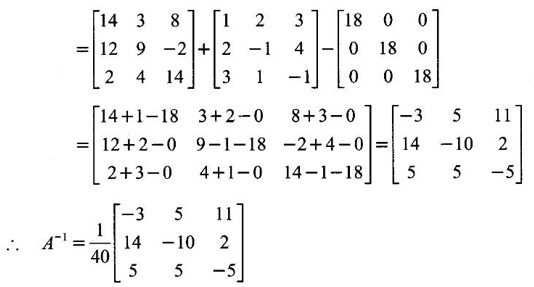
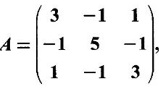 verify Cayley-Hamilton theorem and hence find A-1
verify Cayley-Hamilton theorem and hence find A-1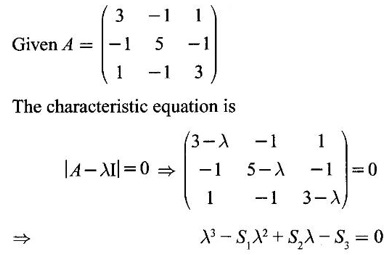
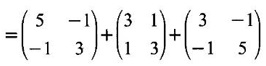
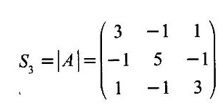

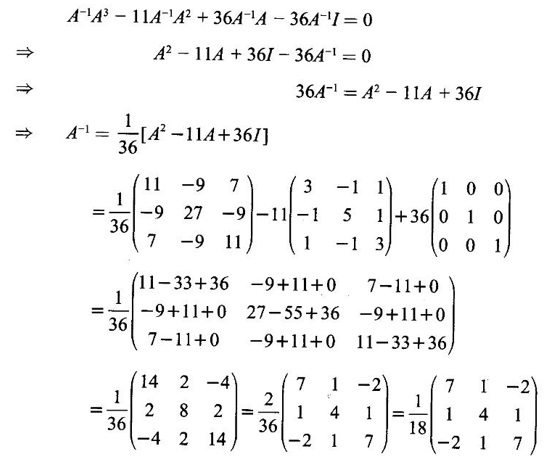
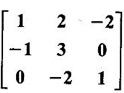

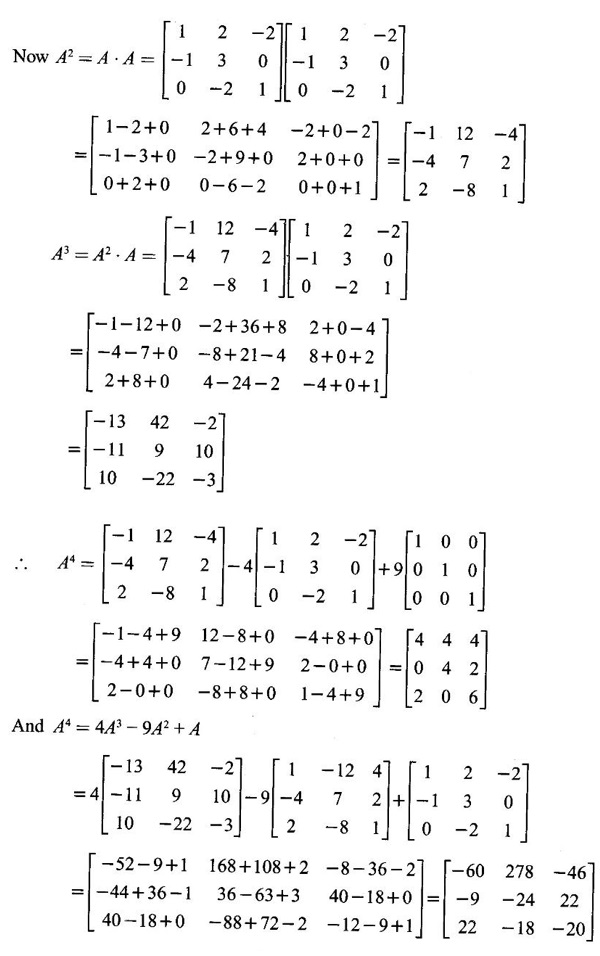
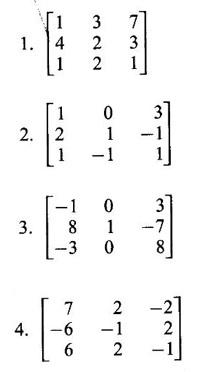
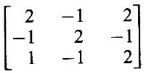 satisfies its characteristic equation and hence find A4.
satisfies its characteristic equation and hence find A4.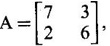 find An in terms of A and I using Cayley-Hamilton theorem and hence find A3.
find An in terms of A and I using Cayley-Hamilton theorem and hence find A3.
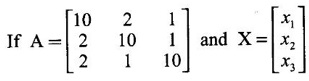 then these equations in matrix form is (A – λI)X = 0 and so | A – λI | = 0 is the characteristic equation of A and λ = 8, 9, 13. Eigen vectors are given by (I)]
then these equations in matrix form is (A – λI)X = 0 and so | A – λI | = 0 is the characteristic equation of A and λ = 8, 9, 13. Eigen vectors are given by (I)]
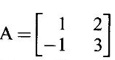 and find its inverse and also find A6 – 4A5 + 8A4 – 12A3 + 14A2.
and find its inverse and also find A6 – 4A5 + 8A4 – 12A3 + 14A2.
Matrices and Calculus: Unit I: Matrices : Tag: : Worked Example Problems - Cayley-Hamilton Theorem
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
