Theory of Machines: Unit III: Friction in Machine Elements
braking of a vehicle
Friction in Machine Elements - Theory of Machines
When the brakes are applied to a moving vehicle the speed decreases and retardation is produced.
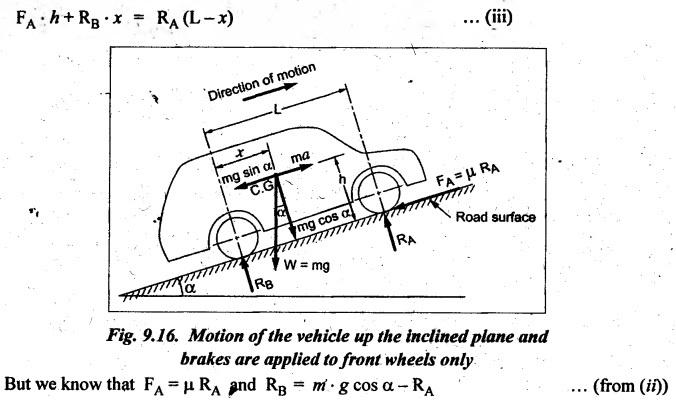
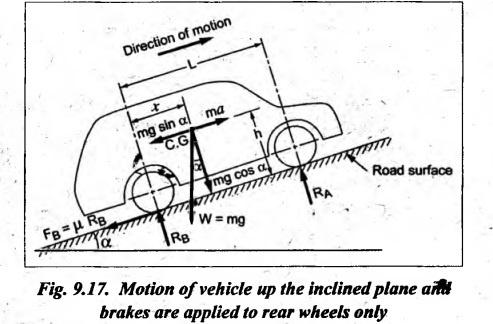
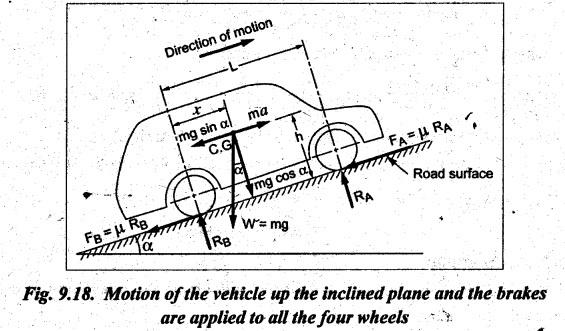
BRAKING OF A VEHICLE When the brakes are applied to a moving vehicle the speed decreases and retardation is produced. The retardation (which is a problem of dynamics) can be reduced to an equivalent static system by applying D'Alembert's principle i.e., by including the inertia force in the system of forces. The effect of brake i.e., the retardation will be determined in the following three cases, both for upward and downward motions. 1. Brakes applied to front wheels, 2. Brakes applied to rear wheels, and 3. Brakes applied to all four wheels. In all these cases, the braking force acts in the opposite direction to the direction of motion of the vehicle. Let α = Angle of inclination of the plane to the horizontal, m = Mass of the vehicle W = m g = Weight of the vehicle, h = Height of C.G. of the vehicle above the road surface, x = Perpendicular distance of C.G. from the rear axle, L = Wheel-base of the vehicle (i.e., distance between the centres of the front and rear wheels), RA = Total normal reaction between the ground and the front wheels, RB = Total normal reaction between the ground and the rear wheels, μ = Coefficient of friction between the types and road surfaces, a = Retardation of the vehicle, FA = μ RA = Total braking force acting at the front wheels due to the application of brakes, and FB = μ RB = Total braking force acting at the rear wheels due to the application of brakes. Case I: When the Brakes are Applied to the Front Wheels Only Consider a car moving up an inclined plane. For the equilibrium of the vehicle, the various forces acting on the vehicle are shown in Fig.9.16. Resolving the forces parallel to the plane, we get Resolving the forces perpendicular to the plane, we get Taking moments about C.G., we get Substituting these values in equation (iii), we get From equation (i), the retardation of vehicle is given by Substituting the values of RA, we get Note: 1. When the vehicles moves on a level track, then α = 0 2. When the vehicle moves down the plane, then equation (i) becomes FA – m • g sin α = m • a Case II: When the Brakes are Applied to the Rear Wheels Only Consider a car moving up an inclined plane. For equilibrium of the vehicle, the various forces acting on the vehicle are shown in Fig.9.17. Resolving the forces parallel to the plane, we get Resolving the forces perpendicular to the plane, we get Taking moments about C.G, we get Substituting these values in equation (iii), we get From equation (1), the retardation of vehicle is given by Substituting the values of RB, we get Note 1. When the vehicle moves on a level track, then α = 0. 2. If the vehicle moves down the plane, then equation (i) becomes Case III: When the Brakes are Applied to All the Four Wheels Consider a car moving up an inclined plane. For the equilibrium of the vehicle, the various forces acting on the vehicle are shown in Fig.9.18. Resolving the fortes parallel to the plane, we get Resolving the forces perpendicular to the plane, we get Taking moments about C.G, we have Substituting these values in equation (iii), we get From equation (i), the retardation of the vehicle is given by Note 1. When the vehicle moves on a level track, then α = 0. 2. If the vehicle moves down the plane, then equation (i) becomes Table 9.1 summarises the expressions used for determining the retardation of the vehicle for different cases. Table 9.1. Formulae summary Example 9.8 A car moving along a level road is having the following data: Wheel base of car 2.85 m; Height of CG from road surface = 600 mm; Perpendicular distance of CG from rear axle = 1.2 m, Speed = 60 km/h; μ = 0.1. Find the minimum distance in which the car may be stopped when brakes are applied, (a) to the rear wheels; (b) to the front wheels, and (c) to all the four wheels. Given data: α = 0°; L = 2.85 m; h = 600 mm = 0.6 m; x = 1.2 mm; u = 60 km/hr = 60 × 1000/3600 1= 6.67 m/s; μ = 0.1 Solution: (a) When brakes are applied to the rear wheels only: We know that retardation when a = 0° and when brakes are applied to the rear wheels, We know that for uniform retardation, (b) When brakes are applied to the front wheels only: We know that retardation when α = 0° and when brakes are applied to the front wheels, (c) When brakes are applied on all four wheels: We know that retardation when α = 0° and when brakes are applied on all four wheels, α = μg = 0.1 × 9.81 = 0.981 m/s2 Note The resistance (ie., braking torque) offered by the wheel bearings against the motion of the vehicles is known as tractive resistance.

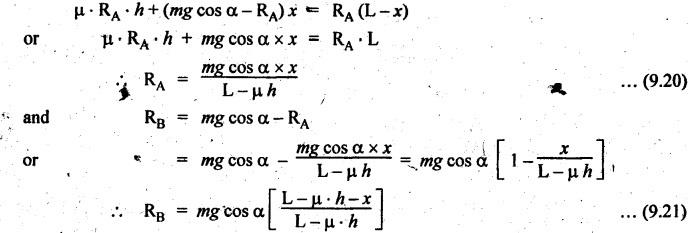
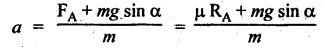
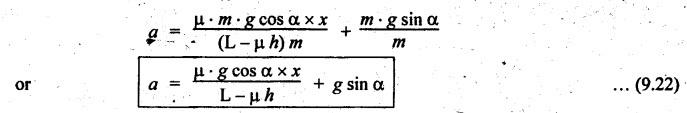
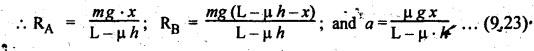
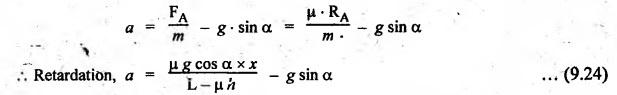


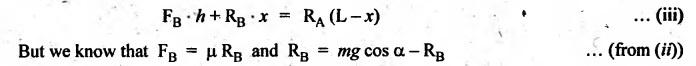
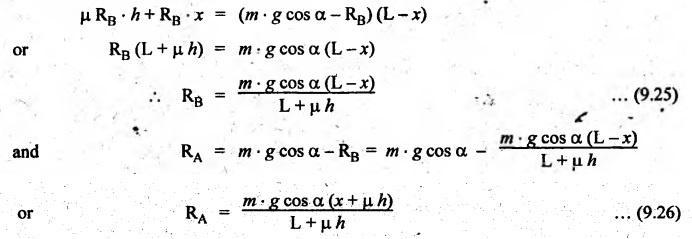
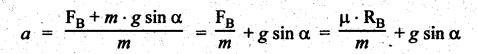
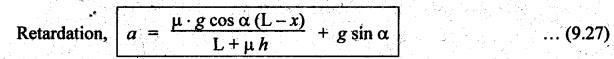
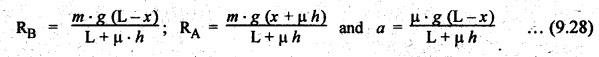
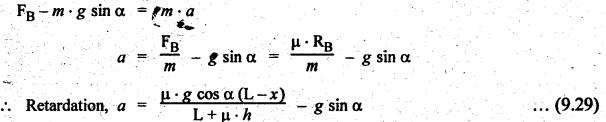


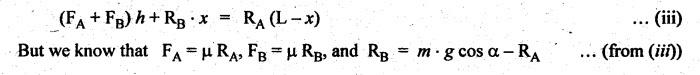
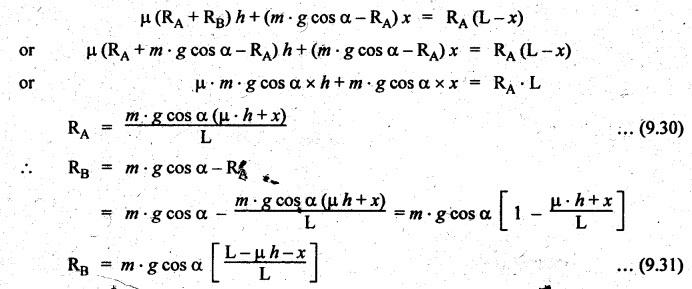
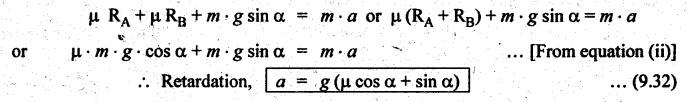
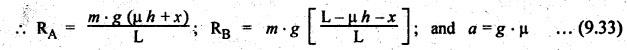
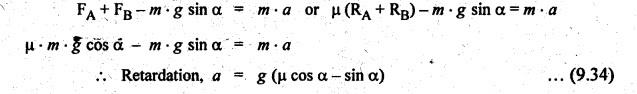
1. Formulae Summary

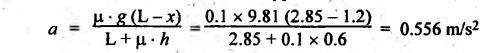
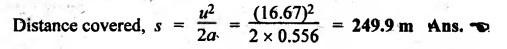
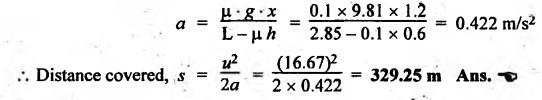
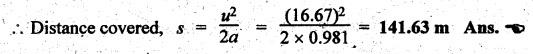
Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - braking of a vehicle
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
