Basic Electrical and Electronics Engineering: Unit IV: Digital Electronics
Boolean Algebra
Basic operations, Theorem, Formula, Truth Table, Solved Example Problems
Boolean algebra is used to analyse and simplify the digital circuits.
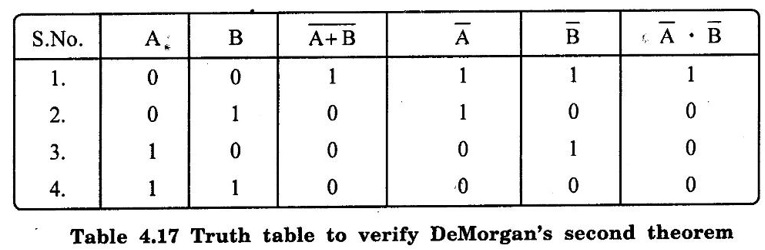
BOOLEAN ALGEBRA ● Boolean algebra is used to analyse and simplify the digital circuits. ● Boolean algebra is invented by George boole in 1854. ● In Boolean algebra, there are three basic operatoins: 1. Logical addition (OR operation) 2. Logical multiplication (AND operation) 3. Logical inversion (NOT operation) Three of the basic laws of boolean algebra are the same as in ordinary algebra. These are commutative laws, associative laws, and distributive laws. This law states that changing the sequence of the variables does not have any effect on the output of logic circuit. Commutative law of addition of two variables: A + B = B + A Commutative law of multiplication of two variables A. B = B. A This law states that the order in which the logic operations are performed is irrelevent as their effect is same. (a) (A . B) C = A . (B . C) (b) (A + B) + C = A + (B + C) Missing 4.47 The distributive law states that A. (B + C) = AB + AC ppppp pppppp ppppppp For simplification of Boolean expressions, we take help of following rules/ theorems. Theorem 1: Idempotent laws (i) A + A = A (ii) A. A = A (i) A + A = A Proof : (ii) A. A = A Proof Theorem 2 : A + 1 = 1 Proof : A + 1 = (A + 1) 1 Theorem 3: A.0 = 0 Theorem 4: Absorption law (1) A + AB = A (2) A (A + B) = A (3) A (Ā + B) = AB (4) (A + B) (A + C) = A + BC 1. A + AB = A Proof : A + AB = A.1 + AB = A(1 + B ) = A.1 since 1+ B = 1 A + AB = A 2. A (A + B) = A Proof : A (A + B) = A.A + AB = A + AB = A (1 + B) since AA = A = A 1 + B = 1 3. A (Ā + B) = AB Proof : = AB 4. (A + B) (A + C) = A + BC We have L.H.S. = (A + B) (A + C) = A.A + A.C + B.A + B.C But AA = A and B.A = A.B Therefore L.H.S = A + AC + AB + BC But A + AB = A Therefore LHS = A + AC+ BCA (1 + C) + BC But (1 + C) = 1 Hence, L.H.S = A + BC Therefore, (A + B) (A + C) = A + BC Theorem: 5 = A + B.1 = A + B According to the duality theorem, the following conversions are possible in a given Boolean expression : (i) We can change each AND operation to an OR operation. (ii) We can change each OR to an AND operation. (iii) We can complement any 1 or 0 appearing in the expression. If the given expression is A + 1 = 1, then, we replace the OR (+) operation by AND (•) operation and take complement of 1 to write the dual of the given relation as under: A • 0 = 0 The dual of A (B + C) = AB + AC is given by A+ (B • C) = (A + B) • (A + C) Problem 4.35 Find the dual of following Boolean expressions : 1. A + AB = A 2. A + ĀB = A + B 3. A + Ā = 1 4. (A + B) (A + C) = A + BC Solution: 1. A + AB = A Let us replace (+) by (•) and (•) by (+) to obtain the dual of the given equation as under : 4.15. A. (A + B) = A [Ans] Similarly, the dual of the other expressions may be obtained as shown in Table 4.15. Theorem 2: This theorem states that the complement of a sum is equal to the product of complements. Figure 4.4 illustrates this theorem. The LHS of this theorem represents a NOR gate with inputs A and B whereas the RHS represents an AND gate with inverted inputs. This AND gate is known as Bubbled AND. Therefore, we can state DeMorgan's second theorem as under: Verification of the Second Theorem Problem 4.36 Prove that A + ĀB + AB = A + B. Solution : L.H.S. = A + ĀB + AB = A + B (Ā + A) But, Ā + A = 1 Therefore, LHS = A + B = RHS Problem 4.37 Simplify: ABCD + Solution : Therefore, Y = ACD Problem 4.38 Simplify the following Boolean expressions: Solution: Problem 4.39 Prove the following Boolean identities : Solution: Problem 4.40 Simplify the following Boolean expression : Y = (AB + C) (AB + D). Solution : Y = (AB + C) (AB + D) = AB AB + ABD + ABC + CD But A . A A and B. B = B Therefore, Y = AB + ABD + ABC + CD = AB (1 + D + C) + CD But, (1 + D + C) = 1 Therefore, Y = AB (1) + CD = AB + CD [Ans] Problem 4.41 Using De Morgan's theorem simplify : Solution: Problem 4.42 Minimize the following function using Boolean algebra. Solution : Arranging the equation, we have Problem 4.43 Simplify the following logic expressions using Boolean algebra. F = AB + A (B + C) + B (B + C) Solution : Applying the distributive law to the second and third terms in the given expression, the expression becomes Z = AB + AB + AC + B. B + BC = AB + AB+ AC + B+ BC [ ⸪ B. B = B] = AB + AC + B + BC [⸪ AB + AB = AB] = AB + AC + B (1 + C) [⸪ 1 + C = 1] = AB + AC + B. 1 [ ⸪ B. 1 = B] = AB + AC + B [⸪ (1 + A) = 1] = B (1 + A) + AC = B + AC [Ans.]Boolean Algebra Laws
1. Commutative law :
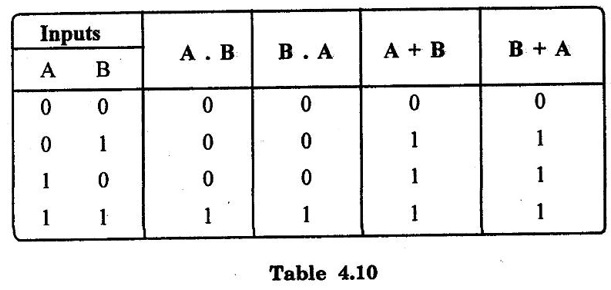
2. Associative law :
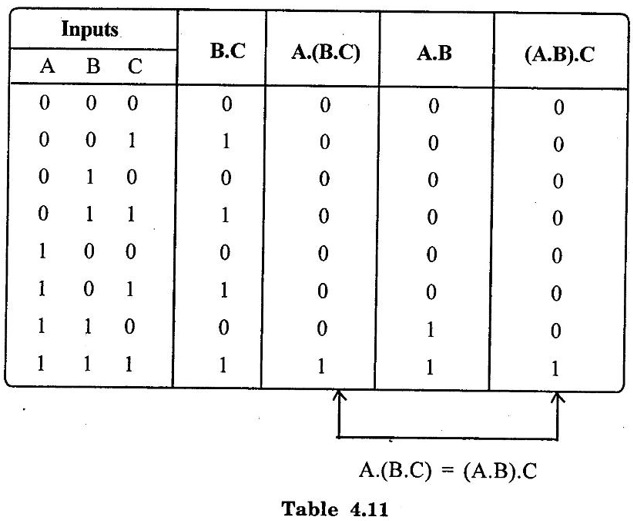

3. Distributive law :
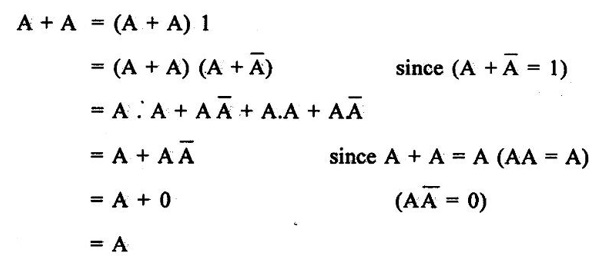
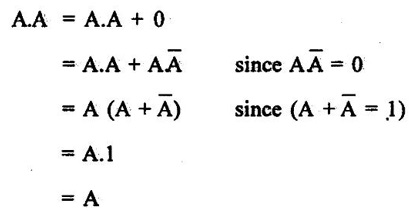
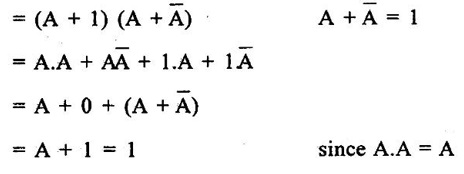
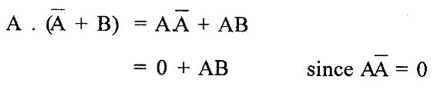
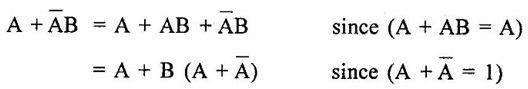
1. Duality Theorem
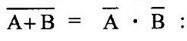 NOR = Bubbled AND
NOR = Bubbled AND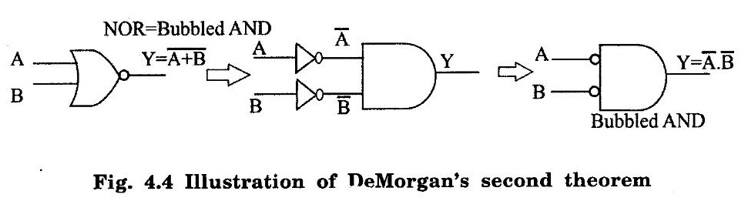
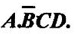
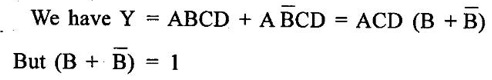
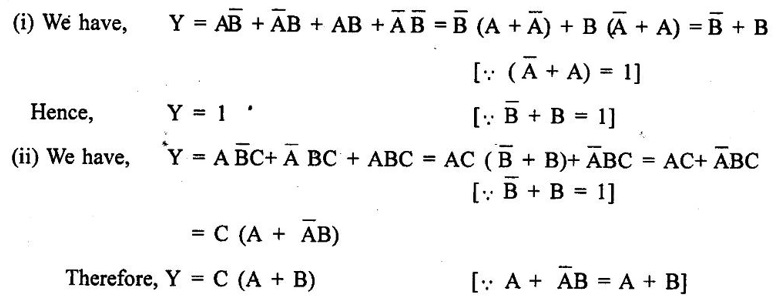
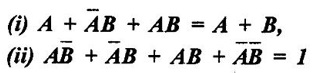

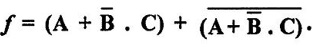

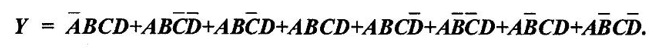
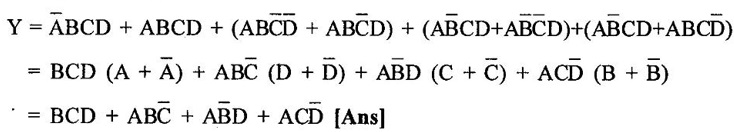
Basic Electrical and Electronics Engineering: Unit IV: Digital Electronics : Tag: : Basic operations, Theorem, Formula, Truth Table, Solved Example Problems - Boolean Algebra
Related Topics
Related Subjects
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

