Engineering Physics: Unit V: Applied Quantum Mechanics
Bloch's Theorem for Particles in a Periodic Potential
Statement, Proof, Definition
The motion of electron inside the lattice is not free as expected, but the electron experiences a periodic potential variation.
BLOCH'S THEOREM FOR PARTICLES IN A PERIODIC POTENTIAL The motion of electron inside the lattice is not free as expected, but the electron experiences a periodic potential variation. The potential energy on the electron is maximum between adjacent ions and gradually decrease as the electron moves towards ions as shown in fig.7.20. It is a mathematical statement regarding the form of one electron wave function for a perfectly periodic potential. If an electron in a linear lattice of lattice constant 'a' characterised by potential function V(x) = V(x + a) satisfies the Schrodinger equation then the wave functions Ψ(x) of electron (with energy E) is obtained as a solution of Schrodinger equation are of the form Here uk (x) is also periodic with lattice periodicity. The potential V(x) is periodic as V(x) = V(x + a) where a is a lattice constant. From the Block theorem, we can say that the free electron is modulated by the periodic function In other words the solutions are plane waves modulated by the function uk (x) which has the same periodicity as the lattice. This theorem is known as Bloch Theorem. The functions of the type (2) are called Bloch functions. If equation (1) has the solution with the property of equation (2), we can write the property of the Bloch functions i.e., equation (3) as Since uk (x + a) = uk (x), we can write the above equation as If Ψ (x) is a single-valued function, then we can write Ψ(x) = Ψ (x + a) Thus Bloch theorem proved. This equation is similar to that of eqn (2) and eqn (4) i.e., If the potential is a function of 'x' and 'a', then the wave function is also a function of ‘x' and 'a'.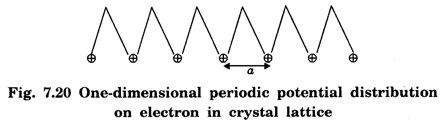
Bloch Theorem
Statement
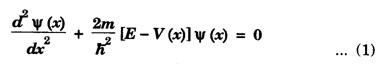
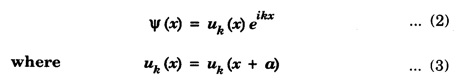
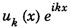
Proof
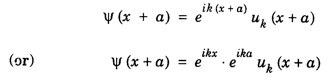

Engineering Physics: Unit V: Applied Quantum Mechanics : Tag: : Statement, Proof, Definition - Bloch's Theorem for Particles in a Periodic Potential
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
