Engineering Physics: Unit V: Applied Quantum Mechanics
Basics of Kronig Penny Model
Applied Quantum Mechanics
The essential feature of the behaviour of electronic potential is studied by considering a periodic rectangular well structure in one dimension.
BASICS OF KRONIG PENNY MODEL The essential feature of the behaviour of electronic potential is studied by considering a periodic rectangular well structure in one dimension. It was first discussed by Kronig and Penny in the year 1931. The potential energy of an electron, when it moves in one dimensional perfect crystal lattice is assumed in the form of rectangular wells as shown in fig. 7.21. In region where 0 < x < a, the potential energy is zero and in the region – b < x < 0, the potential energy is V0. The one dimensional Schrodinger wave equations for two regions are written as For both the regions, the appropriate solution suggested by Bloch is of the form Differentiating equation (5) and substituting in equations (2) and (4), then further solving it under boundary conditions, we get The term P is called as Scattering power of the potential barrier. It is a measure of strength with which the electrons are attracted by the positive ions. From the graph, we conclude that 1. The energy spectrum of an electron consists of a large number of allowed and forbidden energy bands. 2. The width of allowed energy band (shaded portion) increases with increase of energy values i.e., increasing the values of α a. This is because the first term of equation 3. In the limit P → ∞ the allowed energy band reduces to one single energy level corresponding to the discrete energy level of an isolated atom. (ie., a → ∞) 4. In the other extreme case, when P → 0 cos α a = cos ka Thus, a = k which corresponds to free electron model. This indicates that the particle is completely free and no energy levels exist. Thus by varying P from 0 to ∞ we find that the completely free electron becomes completely bound. The energy of the electron in the periodic lattice is given by From the above equation as k changes, the corresponding energy (E) also changes. For a free electron, the energy curve is continuous as shown.. by dotted parabola. But for the electron in the periodic lattice, the energy curve is not a continuous paraboła and discontinuity occur at The zone between 
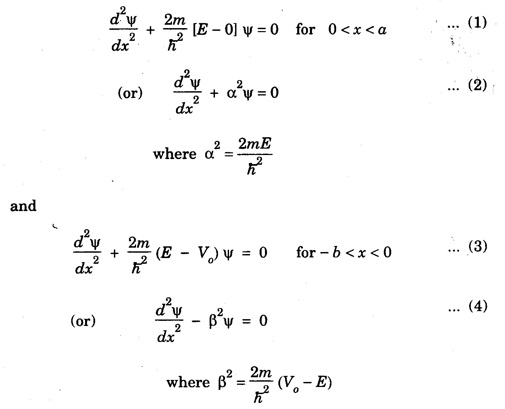

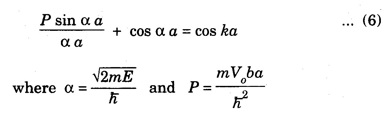

 decreases with increase of α a.
decreases with increase of α a.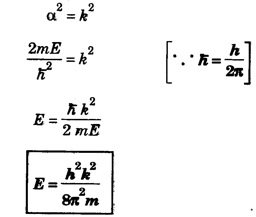
E-K curve

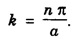
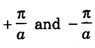 is known as first Brillouin zone and the second zone has two parts from
is known as first Brillouin zone and the second zone has two parts from  and
and  These zones are the allowed energy bands separated by forbidden energy bands as shown in fig. 7.23.
These zones are the allowed energy bands separated by forbidden energy bands as shown in fig. 7.23.
Engineering Physics: Unit V: Applied Quantum Mechanics : Tag: : Applied Quantum Mechanics - Basics of Kronig Penny Model
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
