Strength of Materials: Model Questions Papers
B.E/B.Tech degree examinations april/may 2021
Model Questions Papers - Strength of Materials
B.E/B.Tech degree examinations april/may 2021: Strength of Materials: Model Questions Papers
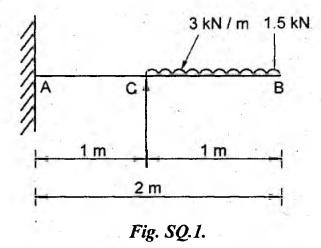
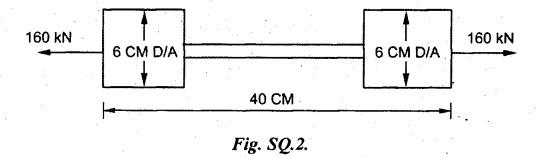
B.E/B.Tech DEGREE EXAMINATIONS APRIL/MAY 2021 Third /Fourth Semester, Aeronautical Engineering STENGTH OF MATERIALS FOR MECHANICAL ENGINEERS (Common to Aerospace Engineering/Automobile Engineering/Industrial Engineering / Industrial Engineering and Management /Manufacturing Engineering / Marine Engineering / Material Science and Engineering / Mechanical Engineering/Mechanical Engineering (Sandwich)/Mechanical and Automation Engineering/Mechatronics Engineering / Production Engineering /Robotics and Automation) Time: Three Hours (Regulations 2017) Answer ALL Questions Maximum : 100 Marks PART – A (10 × 2 = 20 marks) 1. Define Stress. Ans: Refer Question No.1 Page No.1.124 2. What is principle of super position? Ans: Refer Section 1.1.21 Page No.1.21 3. What is meant by transverse loading on beam? Ans: Refer Question No.2 Page No.2.116 4. Define flitched beam. Ans: Refer Question No.6 Page No.2.172 5. Write down the expression for torque transmitted by hollow shaft. Ans: Refer Question No.5 Page No.3.87 6. What are the various types of springs? Ans: Refer Question No.2 Page No.3.140 7. What are the methods for finding out the slope and deflection at a section? The following methods used to finding slope and deflection (i) Double integration method (ii) Macaulay's method (iii) Moment area theorem method (iv) Conjugate beam method 8. When Macaulay's method is preferred? This method is preferred for determining the deflections of a beam subjected to several concentrated loads or a discontinuous load. 9. List out the modes of failure in thin cylindrical shell due to an internal pressure. When the stresses exceed the permissible limit, the cylinder is likely to fail in the following two ways. (i) It may split up into two semicircular halves along the cylinder axis. (ii) It may split up into two cylinders. 10. State Lame's Theorem. Lame's theorem states that if three forces acting at a point are in equilibrium each force is proportional to the sine of the angle between the other two forces. Consider three forces A, B, C acting on a particle or rigid body making angles a, ẞ and y with each other. PART-B (5 × 13 = 65 Marks) 11. (a) A tensile test was conducted on a mild steel bar. The following data was obtained from the test. (i) Diameter of the steel bar = 3 cm (ii) Gauge length of the bar = 20 cm (iii) Load at elastic limit = 250 kN (iv) Extension at a load of 150 kN = 0.21 mm (v) Maximum Load = 380 kN (vi) Total extension = 60 mm (vii) Diameter of rod at failure = 2.25 cm Determine: (1) The Young's modulus (2) The stress at elastic limit (3) The percentage of elongation (4) The percentage decreases in area. Given: To Find: 1. The young's modulus E = ? 2. The stress at elastic limit σE = ? 3. The percentage of elongation = ? 4. The percentage decreases in area = ? Solution: Result: 1. The young's modulus = 2.02 × 105 N/mm2 2. The stress at elastic limit = 353.68 N/mm2 3. The percentage of elongation = 30% 4. The percentage decrease in area = 43.75% [OR] (b) At a certain point in a strained material, the intensities of stresses on two planes at right angles to each other are 20 N/mm2 and 10 N/mm2 both tensile. They are accompanied by a shear stress of magnitude 10 N/mm2, Find the location of principal plane and evaluate the principal stresses. Ans: Refer Example No. 1.81 (Model) Page No. 1.182 12. (a) A cantilever 1.5 m long is loaded with a UDL of 2 kN/m run over a length of 1.25 m from the free end. It also carries a point load of 3 kN at a distance of 0.25 m from the free end. Draw the shear force and bending moment diagrams of the cantilever. Ans: Refer Question No 12 (a), Anna University Solved Question Paper, May/June 2012, Page No. SQ 99 [OR] (b) A rectangular beam 100 mm wide and 250 mm deep is subjected to a maximum shear force of 50 kN. Determine (i) Average shear stress (ii) Maximum shear stress (iii) Shear stress at a distance of 25 mm above the neutral axis. Ans: This question is similar to Example 2.90 Page No. 2.210 13. (a) A hollow shaft of external diameter 120 mm transmits 300 kW power at 200 r.p.m. Determine the maximum internal diameter if the maximum stress in the shaft is not to exceed 60 N/mm2. Given: External Diameter D = 120 mm Power P = 300 kW Speed N = 200 rpm Maximum stress τ = 60 N/mm2 To Find: Internal diameter d = ? Solution: We know that, Shear Stress is given, for hollow shaft d = (62360000)1⁄4 Result: Maximum Internal Diameter of the shaft d = 88.86 mm [OR] (b) Find the expression for the close-coiled helical spring at the centre due to axial load 'W'. Ans: Refer Section No. 3.2.4 Page No.3.92 14. (a) A two metres long cantilever of rectangular section 150 mm wide and 300 mm deep is loaded as shown in figure. Calculate the deflection at the free end. Take E = 10.5 GN/m2. Given: To Find: Deflection at the free end y = ? Solution: We know that (i) The deflection at free end due to point load of 1500 N is given by (ii) The deflection at the free end due to Udl of 3 kN/m over a length of 1m from the free end is given by, Total deflection at the free end y = y1 + y2 = 1.13 + 1.44 Result: Deflection at the free end y = 2.57 mm [OR] (b) A simply supported beam of span 'I is carrying concentrated 'W' at the centre and a UDL of intensity of 'w' per unit length. Show that Maxwell's reciprocal theorem holds good at the centre of the beam. Ans: This question is similar to Example 4.15 Page No. 4.97 15. (a) A cylindrical Shell 3 m long which is closed as the ends an internal diameter of one metre and a wall thickness of 15 mm. Calculate the circumferential and longitudinal stresses induced and also changes in the dimensions of the shell, if it is subjected to an internal pressure of 1.5 N/mm2 and μ = 0.3. Ans: Refer Example No. 5.8 (Model) Page No. 5.13 [OR] (b) Find the thickness of metal necessary for a cylindrical shell of internal diameter 160 mm to withstand an internal pressure of 8 N/mm2. The maximum hoop stress in the stress in the section is not exceed 35. N/mm2. Ans: Refer Example No. 5.28 (Model) Page No. 5.46 PART - C (1 × 15 = 15 Marks) 16. (a) The bar shown in figure is subjected to a tensile load of 160 kN. If the stress in the middle portion is limited to 150 N/mm2. Determine the diameter of the middle portion. Find also the length of the middle portion if the total elongation of the bar is to be 0.2 mm. Young's modulus is given as equal to 2.1 × 105 N/mm2. Ans: Refer Example No. 1.9 Page No. 1.16 [OR] (b) A simply supported beam of length 4 m carries a point load of 3 kN at a distance of 1 m from each end. If E = 2 × 105 N/mm2 and I = 108 mm4 for the beam, then using conjugate beam method determine: (i) Slope at each end and under each load. (ii) Deflection under each load and at the centre. Ans: Refer Question No. 14. (b), Anna University Solved Question paper, Nov/Dec 2014, Page No SQ.152



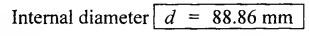

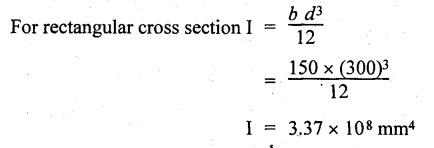

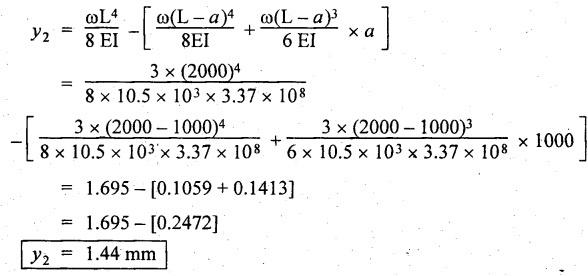
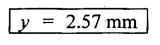
Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E/B.Tech degree examinations april/may 2021
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
