Strength of Materials: Model Questions Papers
B.E/B.Tech degree examination, nov/dec 2015
Model Questions Papers - Strength of Materials
B.E/B.Tech degree examination, nov/dec 2015: Strength of Materials: Model Questions Papers
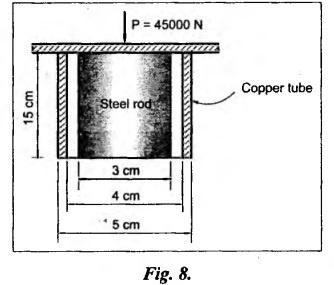
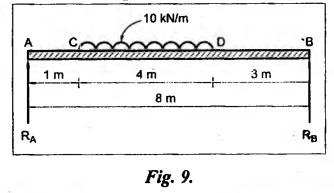
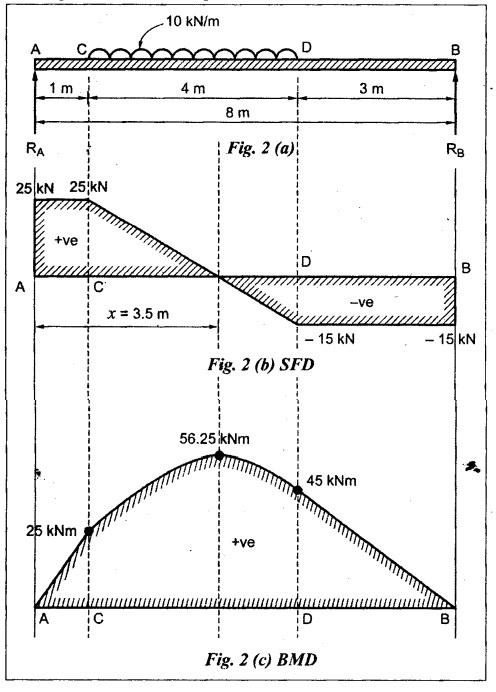
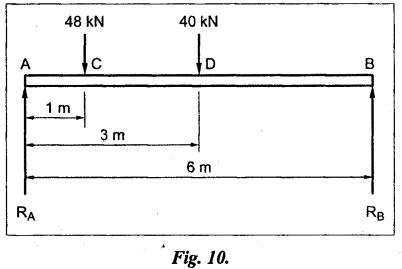
B.E/B.TECH DEGREE EXAMINATION, NOV/DEC 2015 Third Semester (Mech) STRENGTH OF MATERIALS (Common to Mechatronics Engineering, Industrial Engineering and Management Industrial Engineering, Manufacturing Engineering, Mechanical Engineering (sandwich) and Material Science and Engineering) (Regulation 2013) Time: Three hours Answer ALL Questions. Part A (10 × 2 = 20 marks) 1. Differentiate Elasticity and Elastic Limit. Elasticity The property, by virtue of which certain materials return back to their original position after the removal of the external force, is called elasticity. Elastic Limit The value of stress corresponding to this limiting force is known as the elastic limit of the material. 2. What is principle of super position? Ans. Refer Page no. 1.21, Section 1.1.21. 3. Write the assumption in the theory of simple bending? Ans. Refer Page no. 2.172, Question no. 3. 4. What are the types of beams? Ans. Refer Page no. 2.116, Question no. 3. 5. The shearing stress in a solid shaft is not to exceed 40 N/mm2 when the torque transmitted is 20000 N-m. Determine the minimum diameter of the shaft. Ans. Refer Page no. 3.9, Example 3.2. The minimum diameter of shaft [D] = 136.2 mm. 6. What are the various types of springs? Ans. Refer Page no. 3.140, Question no. 2. 7. What are the methods of determining slope and deflection at a section in a loaded beam? Ans. Refer Page no. 4.1, Section 4.1.1. 8. What is the equation used in the case of double integration method? Ans. Refer Page no. 4.5, Section 4.1.4. 9. State the expression for maximum shear stress in a cylindrical shell. Ans. Refer Page no. 5.35, Question no. 5. 10. Define-Hoop stress and longitudinal stress. Ans. Refer Page no. 5.1, Section 5.1.2 (a) and (b). Part B - (5 × 16 = 80 marks) 11. (a) A metallic bar 300 mm × 100 mm × 40 mm is subjected to a force of 50 kN (tensile), 6 kN (tensile) and 4 kN (tensile) along x, y and z directions respectively. Determine the change in the volume of the block. Take E = 2 × 105 N/mm2 and Poisson's ratio = 0.25. Ans. Refer Page no. 1.120, Example 1.60. Change in volume [dV]= 39.339 mm3 [OR] (b) A steel rod of 3 cm diameter is enclosed centrally in a hollow copper tube of external diameter 5 cm and internal diameter of 4 cm as shown in Fig.8. The composite bar is then subjected to axial pull of 45000 N. If the length of each bar is equal to 15 cm, determine: (i) The stresses in the rod and tube, and (ii) Load carried by each bar. Take E for steel = 2.1 × 105 N/mm2 and for copper = 1.1 × 105 N/mm2. Ans. Refer Page no. 1.37, Example 1.23. (i) The stresses in the rod and tube: Stress in the rod [σs] = 41.77 N/mm2 Stress in the tube [σc] = 21.88 N/mm2 (ii) Load carried by each bar: Load on rod [Ps] = 29525.5 N Load on tube [Pc] = 15474.5 N 12. (a) Draw the shear force and B.M diagrams for a simply supported beam of length 8 m and carrying a uniformly distributed load of 10 kN/m for a distance of 4 m as shown in Fig.9. Ans. Refer Page no. 2.63, Example 2.27. [OR] (b) A steel plate of width 120 mm and of thickness 20 mm is bent into a circular arc of radius 10 m. Determine the maximum stress induced and the bending moment which will produce the maximum stress. Take E = 2 × 105 N/mm2. Ans. Refer Page no. 2.137, Example 2.51. Maximum stress [σb max] = 200 N/mm2 Maximum bending moment [Mmax] = 1.6 kNm 13. (a) A hollow shaft of external diameter 120 mm transmits 300 kW power at 200 r.p.m. Determine the maximum internal diameter if the maximum stress in the shaft is not to exceed 60 N/mm2. Ans. Refer Solved Anna University QP, Nov/Dec 06, Question no. 13 (a). The internal diameter [d] = 88.5 mm. [OR] (b) A closely coiled helical spring of mean diameter 20 cm is made of 3 cm diameter rod and has 16 turns. A weight of 3 kN is dropped on this spring. Find the height by which the weight should be dropped before striking the spring so that the spring may be compressed by 18 cm. Take C = 8 × 104 N/mm2. Given Data: To find: Height through which the weight is dropped (h) = ? Solution: Work done by the falling weight on spring Equating the work done by the falling weight on the spring to the energy stored in the spring, we get Result: Height through which the weight W is dropped [h] = 161.7 mm 14. (a) A beam 6m long, simply supported at its ends, is carrying a point load of 50 kN at its centre. The moment of inertia of the beam is given as equal to 78 × 106 mm4. If E for the material of the beam = 2.1 × 105 N/mm2, calculate: (i) deflection at the centre of the beam and (ii) slope at the supports. Ans. Refer Page no. 4.68, Example 4.6. (ii) Slope at the supports: [OR] (b) A beam of length 6 m is simply supported at its ends and carries two point loads of 48 kN and 40 kN at a distance of 1 m and 3 m respectively from the left support as shown Fig.10. Using Macaulay's method find: (i) deflection under each load, (ii) maximum deflection, and (iii) the point at which maximum deflection occurs, Given E = 2 × 105 N/mm2 and I = 85 × 106 mm4. Ans. Refer Anna University Solved Question Paper, Nov/Dec 2008, Question no. 14 (a), 15. (a) A boiler is subjected to an internal steam pressure of 2 N/mm2. The thickness of boiler plate is 2.6 cm and permissible tensile stress is 120 N/mm2. Find the maximum diameter, when efficiency of longitudinal joint is 90% and that of circumference point is 40%. Given Data: Internal steam pressure, P = 2 N/mm2 Thickness of boiler plate, t = 2.6 cm = 26 mm Permissible tensile stress, σc, σa = 120 N/mm2 Efficiency of longitudinal joint, ηl = 90% = 0.90 Efficiency of circumferential joint, ηc = 40% = 0.40 To find: Maximum diameter, d Solution: From equation (1) and (2), maximum diameter of the boiler is equal to the minimum value of diameter. Result: Hence, maximum diameter, d = 2496 mm [OR] (b) Calculate: (i) the change in diameter, (ii) change in length and (iii) change in volume of a thin cylindrical shell 100 cm diameter, 1 cm thick and 5 m long when subjected to internal pressure of 3 N/mm2. Take the value of E = 2 × 105 N/mm2 and Poisson's ratio, μ = 0.3. Ans: Refer Page no. 5.11, Example 5.6. (i) Change in diameter, δd = 0.06375 cm (ii) Change in length, δl = 0.075 cm (iii) Change in volume, δV = 5595.96 cm3
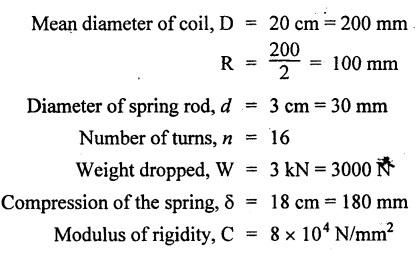

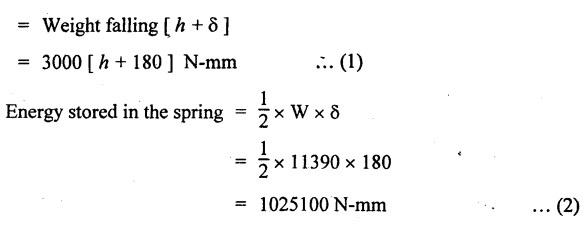
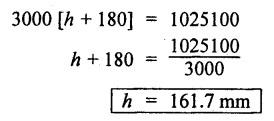
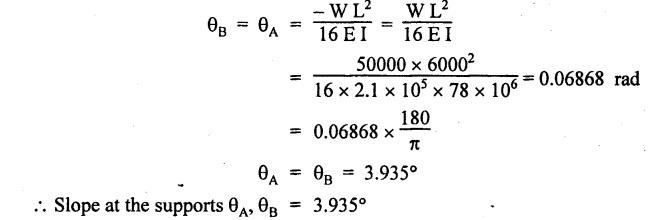


Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E/B.Tech degree examination, nov/dec 2015
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
