Strength of Materials: Model Questions Papers
B.E/B.Tech degree examination, nov/dec 2006
Model Questions Papers - Strength of Materials
Strength of Materials: Model Questions Papers - NOV/DEC 2006 - Strength of Materials: Model Questions Papers
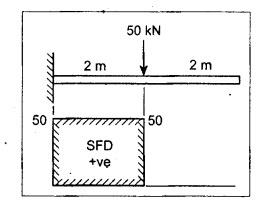
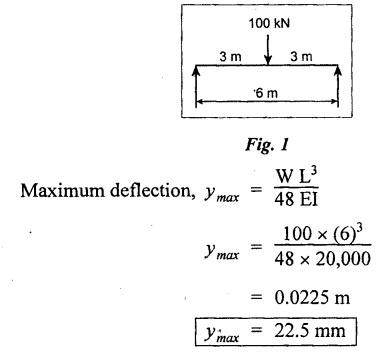
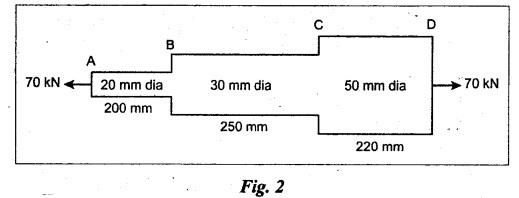
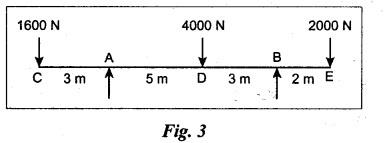
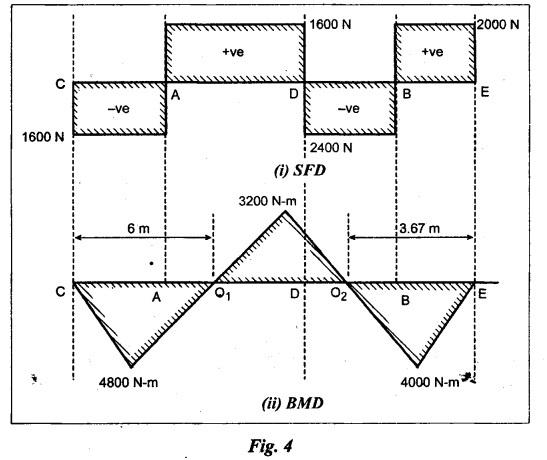
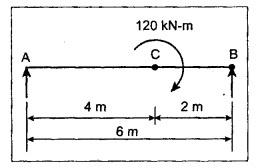
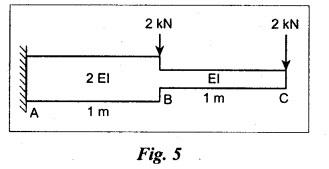
ANNA UNIVERSITY B.E/B.TECH DEGREE EXAMINATION, NOV/DEC 2006 Fourth Semester - Mechanical Engineering CE1262 STRENGTH OF MATERIALS (Common to Mechanical Engineering/Mechatronics Engineering/ Metallurgical Engineering/Production Engineering) (Regulation 2004) Time: Three hours Answer ALL Questions. Part A (10 × 2 = 20 marks) Maximum: 100 Marks 1. Estimate the load carried by a bar if the axial stress is 10 N/mm2 and the diameter of bar is 10 mm. Given: Stress, σ = 10 N/mm2 2. Diameter, D = 10 mm Solution: We know that, 2. What is the strain energy stored when a bar of 6 mm diameter 1 m length is subjected to an axial load of 4 kN, E = 200 kN/mm2. Given: Diameter, D = 6 mm Solution: Volume of the bar, V = A × L = 28.274 × 1000 3. Draw the shear force diagram for a cantilever beam of span 4 m and carrying a point load of 50 kN at midspan. 4. Draw the bending stress and shear stress distribution due to bending of beam with rectangular cross section. Ans. Refer Anna University Solved Question Papers, May/June 2006, Question no. 4. 5. Write the expressions for stiffness of a close coiled helical spring. Ans. Refer Page no. 3.140, Question no. 3. 6. Find the minimum diameter of shaft required to transmit a torque of 29820 Nm if the maximum shear stress is not to exceed 45 N/mm2. Ans. Refer Page no. 3.9, Example 3.2. [Ans. D = 150 mm] 7. Find the critical load of an Euler's column having 4 m length, 50 mm × 100 mm cross section and hinged at both the ends. E = 200 kN/mm2. NOT IN SYLLABUS 8. Calculate the maximum deflection of a simply supported beam carrying a point load of 100 kN at midspan. Span = 6 m, EI = 20,000 kN/m2. 9. Define principal plane and principal stresses. Ans. Refer Page no. 1.124, Question no. 1. 10. Find the thickness of the pipe due to an internal pressure of 10 N/mm2 if the permissible stress is 120 N/mm2. The diameter of pipe is 750 mm. Given: Pressure, p = 10 N/mm2 Stress, σ = 120 N/mm2 Diameter, d = 750 mm Solution: We know that, Part B (5 × 16 = 80 marks) 11. (a) (i) Find the stresses in each section of the bar shown in Fig.2. (ii) Find the total extension of the bar shown in Fig.2. E = 2.1 × 103 N/mm2. Ans. Refer Page no. 1.13, Example 1.7. [Ans. σAB = 222.8 N/mm2; OBC = 99.02 N/mm2; OCD = 35.65 N/mm2; Total elongation, δL = 0.3674 mm] [OR] (b) (i) A steel rod of 25 mm diameter is placed inside a copper tube of 30 mm internal diameter and 5 mm thickness and the ends are rigidly connected. The assembly is subjected to a compressive load of 250 kN. Determine the stresses induced in the steel rod and copper tube. Take the modulus of elasticity of steel and copper as 200 GPa and 80 GPa respectively. Ans. Refer Page no. 1.44, Example 1.27. (10) (ii) Find the total strain energy stored in a steel bar of diameter 50 mm and length 300 mm when it is subjected to an axial load of 150 kN. Take modulus of elasticity of steel as 200 × 103 MPa. (6) 12. (a) Draw the S.F. and B.M. diagrams for the beam shown in Fig.3. Determine the points of contraflexure. Ans. Refer Page no. 2.75, Example 2.31. Reactions, RA = 3200 N RB = 4400 N Point of contraflexure O1, O2. (b) A timber beam of rectangular section is to support a total load of 20 kN uniformly distributed over a span of 3.6 m when the beam is simply supported. If the depth is twice the width of the section and the stress in timber is not to exceed 3.5 N/mm2, find the dimensions of the cross section? Ans. Refer Page no. 2.160, Example 2.65. b = 156.83 mm; d = 313.66 mm. 13. (a) A hollow steel shaft of outside diameter 75 mm is transmitting a power of 300 kW at 2000 rpm. Find the thickness of the shaft if the maximum shear stress is not to exceed 40 N/mm2. Given: D = 75 mm; P = 300 kW Ν = 2000 rpm; τ = 40 N/mm2 To find: Thickness of the shaft, t. Solution: We know that, Result: Thickness, t = 4.95 mm [OR] (b) A close coiled helical spring is to have a stiffness of 1.5 N/mm of compression under a maximum load of 60 N. The maximum shearing stress produced in the wire of the spring is 125 N/mm2. The solid length of the spring is 50 mm. Find the diameter of coil, diameter of wire and number of coils C = 4.5 × 10a N/mm2. Given: To find: 1. Diameter of the coil, D 2. Diameter of the wire, d 3. Number of coils, n Solution: We know that, Substitute d value in equation (1) and (2). Substitute R value in equation (3), Substitute n value in equation (4), Result: 1. n = 15 2. D = 32.72 mm 3. d = 3.42 mm 14. (a) A horizontal beam AB is simply supported at A and B, 6 m apart. The beam is subjected to a clockwise couple of 300 kN-m at a distance of 4 m from the left end A. If E = 2 × 105 N/mm2 and I = 2 × 108 mm4. Determine, using Macaulay's method, (i) The deflection at a point where couple is acting. (ii) The maximum deflection. Given Data: E = 2 × 105 N/mm2 and I = 2 × 108 mm4 To find: 1. Deflection at C = ? 2. Maximum deflection = ? Solution: Taking moment about A, Applying the following boundary conditions, (i) When x = 0, y = 0 and (ii) When x = 6m, y = 0 Applying the first boundary condition in equation (3), 0 = C2 Now equation (3) reduces to Applying the second boundary condition in equation 4, The slope becomes zero where the maximum deflection occurs. Therefore, dy / dx = 0 Applying this condition in equation (2), Therefore, the maximum deflection occurs at a distance of 4.233 m from B, ymax = 0.016 mm [OR] (b) For the cantilever beam shown in Fig.5, find the deflection and slope at the free end. EI= 10000 kN/m2. Solution: (Moment Area Method) 15. (a) The normal stresses in two mutually perpendicular directions are 110 N/mm2 and 47 N/mm2 both tensile. The complementary shear stresses in these directions are of intensity 63 N/mm2. Find the principal stresses and its planes. Ans. Refer Page no. 1.175, Example 1.75. [OR] (b) A cylindrical shell 3 m long which is closed at the ends has an internal diameter 1 m and wall thickness of 15 mm. Calculate the change in dimensions and change in volume if the internal pressure is 1.5 N/mm2. E = 2 × 105 N/mm2. v = 0.3. Ans. Refer Page no. 5.11, Example 5.6. (i) Change in diameter, δd = 0.2125 mm (ii) Change in length, δl = 0.15 mm (iii) Change in volume, δv = 1119192.38 mm3
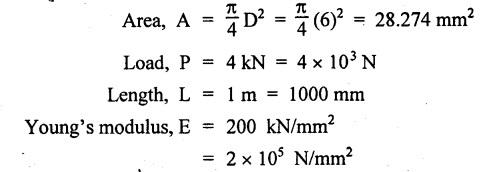

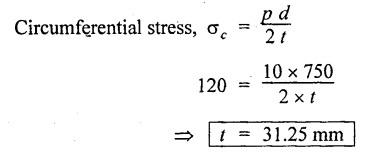




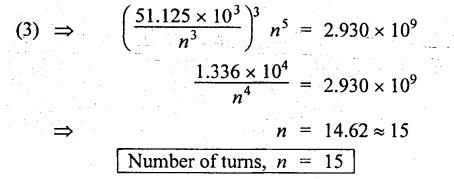


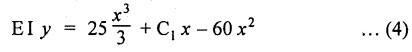



Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E/B.Tech degree examination, nov/dec 2006
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
