Strength of Materials: Model Questions Papers
B.E/B.tech. degree examination, april/may 2008
Model Questions Papers - Strength of Materials
Model Questions Papers - Strength of Materials : B.E/B.tech. degree examination, april/may 2008
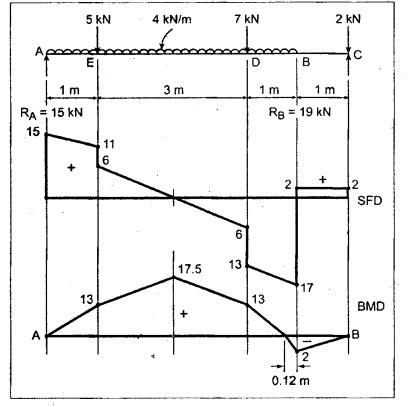
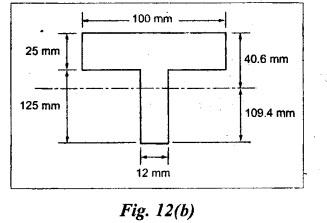
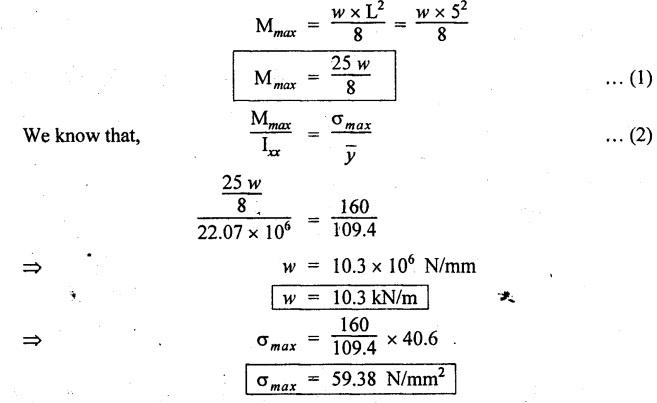
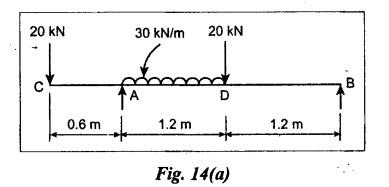
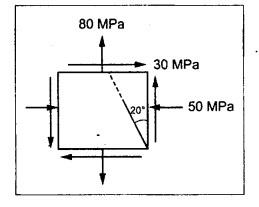
ANNA UNIVERSITY B.E/B.Tech. DEGREE EXAMINATION, APRIL/MAY 2008 Fourth Semester - Automobile Engineering STRENGTH OF MATERIALS (Common to Mechanical Engineering/Mechatronics Engineering/ Metallurgical Engineering/Production Engineering) (Regulation 2004) Time: Three hours SQ.39 Maximum: 100 Marks Answer ALL Questions. Part A (10 × 2 = 20 marks) 1. The Young's modulus and the shear modulus of material are 120 GPa and 45 GPa respectively. What is its Bulk modulus? Ans. Given: Young's modulus, E = 120 GPa = 120 × 109 Pa = 120 × 109 N/m2 = 120 × 103 N/mm2 Shear modulus, G = 45 Gpa = 45 × 103 N/mm2 Solution: 2. Calculate the instantaneous stress produced in a bar of cross sectional area 1000 mm2 and 3 m long by the sudden application of a tensile load of unknown magnitude, if the instantaneous extension is 1.5 mm. Also find the corresponding load. Take E = 200 GPa. Given: A = 1000 mm2 L = 3 m = 3000 mm δL = 1.5 mm E = 200 GPa = 200 × 103 N/mm2 Solution: 3. Define point of contraflexure. Ans. Refer Page no. 2.122, Question no. 25. 4. A rectangular beam 100 mm wide and 250 mm deep is subjected to a maximum shear force of 50 kN. What is the shear stress at a distance of 25 mm above the neutral axis? Ans. Refer Page no. 2.193, Example 2.77. 5. Define polar modulus of a section. What is the polar modulus value for a hollow circular section of 100 mm external diameter and 40 mm internal diameter. Ans. It is the ratio between polar moment of inertia and the maximum radius of a circular section. 6. A close coiled helical spring is to carry an axial load of 500 N. Its mean coil diameter is to be 10 times its wire diameter. Calculate these diameters if the maximum shear stress in the material is to be 80 MPa. Ans. Given: W = 500 N D = 10 d τ = 80 MPa = 80 × 106 Pa = 80 × 106 N/m2 = 80 N/mm2 Solution: We know that, 7. In a simply supported beam of 3 m span carrying uniformly distributed load throughout the length, the slope at the supports is 1°. What is the maximum deflection in the beam? Ans. Given: Solution: We know that, 8. State any two assumptions made in Euler's column theory. NOT IN SYLLABUS 9. A spherical shell of 1 m internal diameter undergoes a diametral strain of 10-4 due to internal pressure. What is the corresponding change in its internal volume? Ans. Change in volume, dV = ev × V = 3 × e × V 10. A thin cylinder closed at both ends is subjected to an internal pressure of 2 MPa. Its internal diameter is 1 m and the wall thickness is 10 mm. What is the maximum shear stress in the cylinder material? Ans. Given: Solution: Part – B (5 × 16 = 80 marks) 11. (a) A compound bar is constructed from three bars each 50 mm wide and 12 mm thick fastened together to form a bar 50 mm wide and 36 mm thick. The middle bar is of aluminium for which E = 70 GPa and the outer bars are of brass for which E = 100 GPa. If the bars are initially fastened at 18°C and the temperature of the whole assembly is then raised to 50°C, determine the stresses set up in brass and aluminium. Take the coefficient of linear expansion as 18 × 10-6 for brass and 22 × 10-6 for aluminium. What will be the changes in these stresses if an external compressive load of 15 kN is then applied on the bar? Ans. From given data, we know that, coefficient of linear expansion αA > αB, so, aluminium will be in compression and brass will be in tension. (b) A 25 mm diameter bar is subjected to an axial tensile load of 100 kN. Under the action of this load a 200 mm gauge length is found to extend 0.19 mm. Determine the modulus of elasticity of the material. If in order to reduce weight whilst keeping the external diameter constant, the bar is bored axially to produce a hollow cylinder of uniform thickness, what is the maximum diameter of bore possible given that the maximum allowable stress is 240 MPa? The load can be assumed to remain constant at 100 kN. What will be the change in the outer diameter of the bar under the above load? Taking Poisson's ratio 0.3, also calculate the Bulk modulus and the shear modulus of the material. Ans. We know that, With bore of diameter D. We know that, 12. (a) For the beam shown in Fig.12(a), draw the shear force and bending moment diagrams, showing all salient values on them. Ans. Refer Page no. 2.109, Example 2.39. [OR] (b) A uniform T section beam is 100 mm wide and 150 mm deep with a flange thickness of 25 mm and a web thickness of 12 mm. If the limiting bending stress is 160 MPa in tension, find the maximum uniformly distributed load that the beam can carry over a simply supported span of 5 m. Also determine the corresponding maximum bending stress in compression. (12+4) Ans. For uniformly distributed load, 13. (a) Determine the dimensions of a hollow circular shaft with a diameter ratio of 3: 4 which is to transmit 60 kW at 200 rpm. The maximum shear stress in the shaft is limited to 70 GPa and the angle of twist to 3.8° in a length of 4 m. For the shaft material the modulus of rigidity is 80 GPa. Given: l = 4 m = 4000 mm c = 80 GPa = 80 × 103 N/mm2 To find: (i) External diameter, D (ii) Internal diameter, d Solution: We know that, Result: External diameter, D = 75.39 mm Internal diameter, d = 56.54 mm [OR] (b) A close coiled helical spring is required to absorb 2250 joules of energy. Determine the diameter of the wire, the mean coil diameter of the spring and the number of coils necessary if (i) the maximum stress is not to exceed 400 MPa, (ii) the maximum compression of the spring is limited to 250 mm and (iii) the mean diameter of the spring is eight times the wire diameter. For the spring material, rigidity modulus is 70 GPa. Ans. 14. (a) In the beam shown in Fig.14(a), determine the slope at the left end C and the deflection at 1 m from the left end. Take EI = 0.65 MNm2. Ans. [OR] (b) The external and internal diameters of a hollow cast iron column are 50 mm and 40 mm respectively. If the length of this column is 3 m and both of its ends are fixed, determine the crippling load using Euler formula taking E = 100 GPa. Also determine the Rankine load for the column assuming ƒc = 550 MPa and a = 1/1600. NOT IN SYLLABUS 15. (a) A cylinder has an internal diameter of 230 mm, wall thickness 5 mm and is 1 m long. It is found to change in internal volume by 12 × 10-6 m3 when filled with a liquid at a pressure 'p'. Taking E = 200 GPa and Poisson's ratio = 0.25, determine the stresses in the cylinder, the changes in its length and internal diameter. Given: To find: 1. Longitudinal stress, σa 2. Hoop stress, σc 3. Change in length, δl 4. Change in diameter, δd Solution: We know that, Result: [OR] (b) A material is subjected to two mutually perpendicular direct stresses of 80 MPa tensile and 50 MPa compressive, together with a shear stress of 30 MPa. The shear couple acting on planes carrying the 80 MPa stress is clockwise ineffect. Find (i) principle stresses, (ii) the maximum shear stress, (iii) the normal stress on the plane of maximum shear, (iv) the stresses on a plane at 20°counterclockwise to the plane on which the 50 MPa stress acts. Ans. Normal stress on max. shear plane Normal stress on inclined plane Shear stress on inclined plane

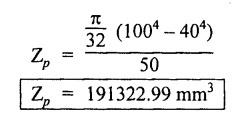
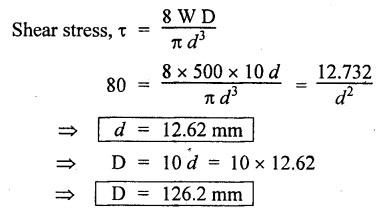


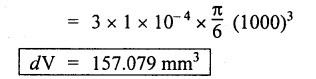


 [OR]
[OR]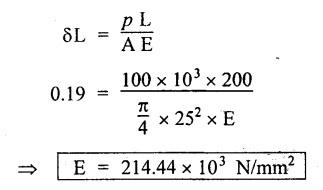
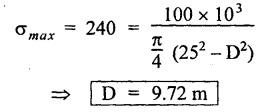

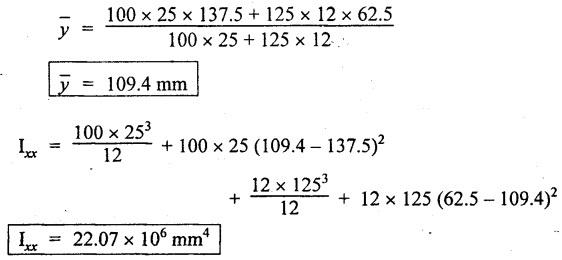
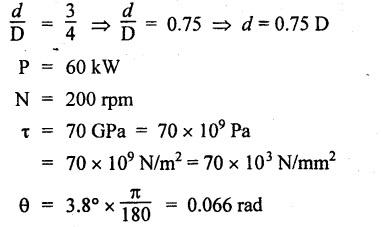





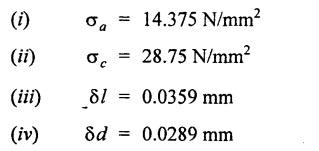
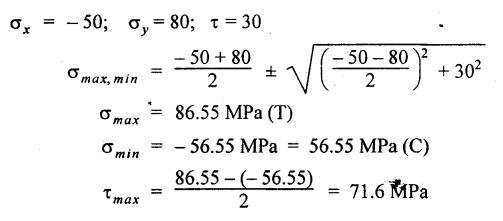
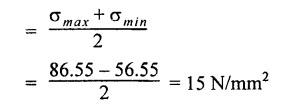

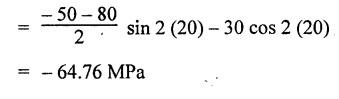
Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E/B.tech. degree examination, april/may 2008
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
