Strength of Materials: Model Questions Papers
B.E./B.Tech. degree examinations, april/may 2019
Model Questions Papers - Strength of Materials
B.E./B.Tech. degree examinations, april/may 2019: Strength of Materials: Model Questions Papers
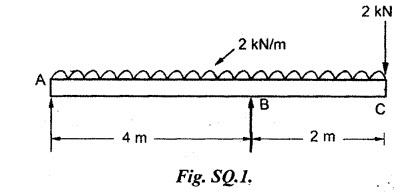
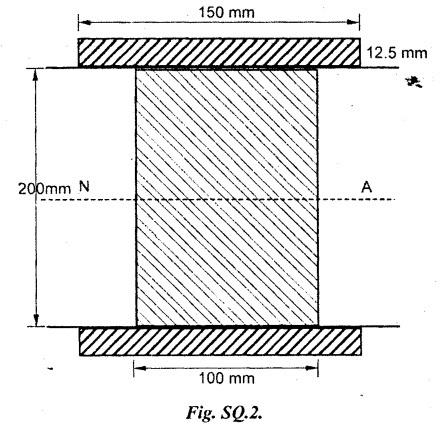
B.E./B.Tech. DEGREE EXAMINATIONS, APRIL/MAY 2019 Third/Fourth Semester Mechanical Engineering STRENGTH OF MATERIALS FOR MECHANICAL ENGINEERS (Common to Aeronautical Engineering/Automobile Engineering / Industrial Engineering / Industrial Engineering and Management / Manufacturing Engineering / Marine Engineering / Material Science and Engineering / Mechanical Engineering(Sandwich/Mechanical and Automation Engineering / Mechatronics Engineering/Production Engineering / Robotics and Automation Engineering) Time: Three hours PART A - (10 x 2 = 20 marks) 1. What do you meant by thermal stress? Ans: Refer Section No: 1.1.27 in Page No: 1.51 2. Define principal plane and principal stresses. Ans: Refer Question No: 1 in Page No: 1.192 3. What is meant by point of contra-flexure? Ans: Refer Question No: 25 in Page No: 2.122 4. What is ratio of maximum shear stress to the average shear stress in the case of solid circular section? Ans: Refer Question No: 7 in Page No: 2.214 5. Write down the expression for power transmitted by a shaft. Ans: Refer Question No: 4 in Page No: 3.86 6. Define helical springs. A helical spring is a length of wire (or) bar wound into a helix. There are mainly two types of helical springs. (i) Close-coiled helical spring (ii) Open-coiled helical spring 7. A beam 3 m long, simply supported at its ends, is carrying a point load W at the centre. If the slope at the beam should not exceed 1°. Find the deflection at the centre of the beam. Given: Span, L = 3 m Slope, θ = 1° Solution: We know that, 8. State Maxwell's reciprocal theorems. Ans: Refer Section No: 4.1.32 in Page No: 4.96 9. Differentiate between a thin cylinder and a thick cylinder. Ans: Refer Question No: 15 in Page No: 5.36 10. State Lame's theorem. (i) The material of the cylinder is homogeneous and Isotropic. (ii) The plane sections of the cylinder, perpendicular to the longitudinal axis remain plane under the effect of pressure i.e. the longitudinal strain is constant and is Independent of radius. The theory derived after above mentioned assumptions is popularly known as Lame's theory. PART B – (5 × 13 = 65 marks) 11. (a) A steel rod of 3 cm diameter and 5 m long is connected to two grips and the rod is maintained at a temperature of 95 °C. Determine the stress and pull exerted when the temperature falls to 30°°C, if (i) the ends do not yield, and (ii) the ends yield by 0.12 cm. take E = 2 × 106MN/m2 and α = 12 × 10−6/°C. Ans: Refer Question No. 1.33 (model) Page No. 1.55 [OR] (b) An elementel cube is subjected to tensile stresses of 30 N/mm2 and 10 N/mm2 acting on two mutually perpendicular plan and a shear stress of 110 N/mm2 on these planes. Draw the Mohr's circle of stresses and hence or otherwise determine the magnitudes and directions of principal stresses and also the greatest shear stress. Ans: Refer Example 1.71 (model) Page No. 1.167 12. (a) Draw the shear force and bending moment diagrams for the overhanging be a carrying uniformly distributed load of 2 kN/m over the entire length and a point load of 2 kN as shown in Figure below. Ans: Refer Example 2.44 Page No: 2.105 [OR] (b) A timber beam 100 mm wide and 200 mm deep is to be reinforced by bolting on two steel flitches each 150 mm by 12.5 mm in section. Calculate the moment of resistance when flitches are attached symmetrically at the top and bottom. Allowable stress in timber is 6 N/mm2. Take Es = 2 × 105 N/mm2 and Et = 1 × 104 N/mm2. Given: Dimensions as shown in Figure. Allowable stress in timber = 6 N/mm2 young's modulus of steel, Es = 2 × 105 N/mm2 young's modulus of timber, Et = 1 × 104 N/mm2 To Find: Moment of resistance when flitched are attached symmetrically at the top and bottom. Solution: Section Modulus Allowable stress for steel section is Maximum stress in steel would be extreme fibre at a distance from N.A. Distance of extreme fibre of timber from N.A. Distance of extreme fibre of steel from N.A We know that, bending stresses are proportional to extreme fibre distance. Moment of resistance of timber section Moment of resistance of steel section, Result: Moment of resistance, MR = 54.85 × 106 N.mm 13. (a) Two shafts of the same material and of same lengths are subjected to the same torque, if the shaft is of a solid circular section and the second shaft is of hollow circular section, whose internal diameter is 2/3 of the outside diameter and the maximum shear stress developed in each shaft is the same, compare the weights of the shafts. Solution: Two shafts of the same material and of same lengths (one is solid and other is hollow circular section) transmit the same torque and develop the same maximum shear stress. Let, T - Torque τ - Maximum shear stress DS - Outer diameter of the solid shaft DO - Outer diameter of the hollow shaft Di - Inner diameter of the hollow shaft WS - Weight of solid shaft Wh - Weight of hollow shaft L - Length of each shaft ρ - Weight density of the material of each shaft Torque transmitted by the solid shaft is given by equation, Torque transmitted by the hollow shaft, As torque transmitted by two shafts are equal Weight of solid shaft, WS = Weight density × volume of solid WS = ρ × Area × Length Weight of hollow shaft, Wh = ρ × Area × Length [OR] (b) A closely coiled helical spring of mean diameter 20 cm is made up of 3 cm diameter rod and has 16 turns. A weight of 3 kN is dropped on this spring. Find the height by which the weight should be dropped before striking the spring so that the spring may be compressed by 18 cm. Take 8 × 104 N/mm2. Ans: Refer Solved Anna University Question Paper Nov/Dec 2015 Question No. 13. (b) 14. (a) A beam of length 5 m and of uniform rectangular section is simply supported at its ends. It carries a uniformly distributed load of 9 kN/m run over the entire length. Calculate the width and depth of the beam if permissible bending stress is 7 N/mm2 and central deflection is not exceed 1 cm. Take E for beam material = 1 × 104 N/mm2 Given: Length, L = 5m = 5000 mm UDL, w = 9 kN/m = 9 × 103 × 10-3 N/mm = 9 N/mm Permissible bending stress, σb = 7 N/mm2 Central deflection, ymax = 1 cm = 10mm young's modulus, E = 1 × 104 N/mm2. To Find: Width and depth of the beam. Solution: We know that, the maximum deflection if the simply supported beam carrying UDL over entire length is The moment of inertia for the rectangular section is From the theory of simple bending equation Dividing the equation (1) and (2) Result Width, b = 182 cm depth, d = 364 mm [OR] (b) A simply supported beam of length 5 m carries a point load of 5 kN at a distance of 3 m from the left end. If E = 2 × 105N/mm2 and I = 108 mm4, determine the slope at the left support and deflection under the point load using conjugate beam method. Ans: This question is similar to Example 4.7 (iv) Page No. 4.72 15. (a) A cylindrical thin drum 80 cm in diamter and 3 m long has a shell thickness of 1 cm. If the drum is subjected to an internal pressure of 2.5 N/mm2, determine (i) Change in diameter (ii) Change in length and (iii) Change in volume Take E = 2 × 105N/mm2, Poisson's ratio = 0.25. Ans: This question is similar to Example 5.6 Page No. 5.11 [OR] (b) A spherical shell of internal diameter 0.9 m and of thickness 10 mm is subjected to an internal pressure of 1.4 N/mm2. Determine the increase in diameter and increase in volume, take E = 2 × 105N/mm2 and μ = 1/3. Ans: This question is similar to Example 5.15 Page No. 5.22 PART C − (1 × 15 = 15 marks) 16. (a) An I-section beam 350 mm × 150 mm has a web thickness of 10 mm and a flange thickness of 20 mm. If the shear force acting on the section is 10 kN, find the maximum shear stress developed in the I-section. Also sketch the shear stress distribution across the section. Ans: This question is similar to Example 2.81 Page No. 2.197 [OR] (b) Derive an expression for the slope and deflection of a simply supported beam subjected to uniformly distributed load. Ans: Refer Section No. 4.1.13 Page No: 4.23
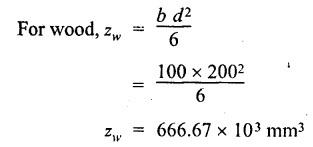
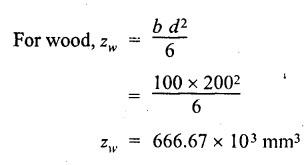
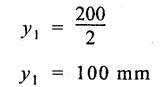
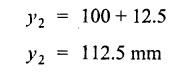
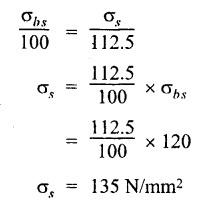
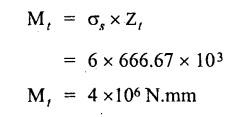
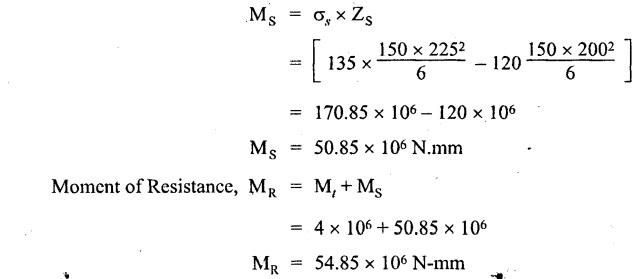
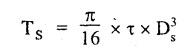
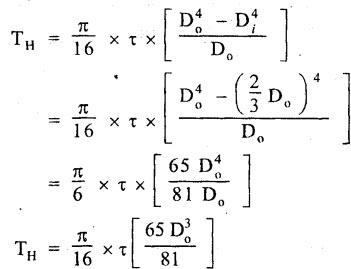
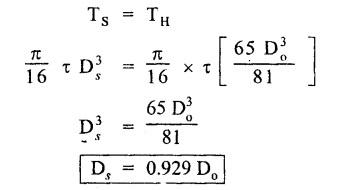


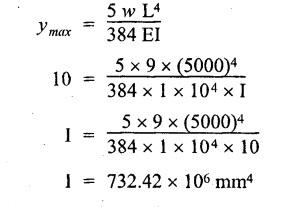
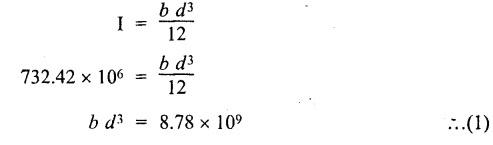


Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E./B.Tech. degree examinations, april/may 2019
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
