Strength of Materials: Model Questions Papers
B.E./B.Tech. degree examination, november/december 2008
Model Questions Papers - Strength of Materials
B.E./B.Tech. degree examination, november/december 2008: Strength of Materials: Model Questions Papers
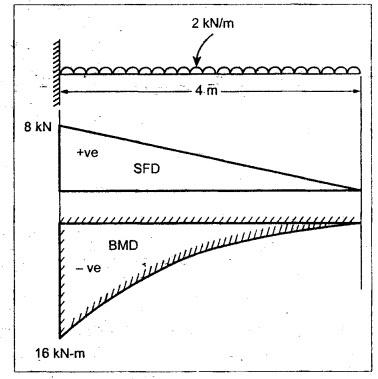
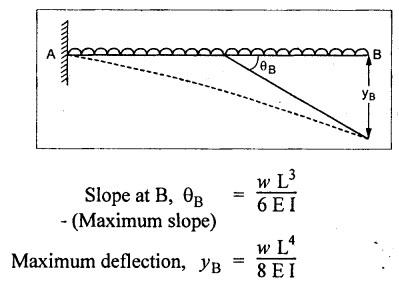
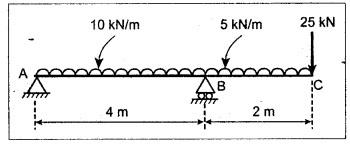
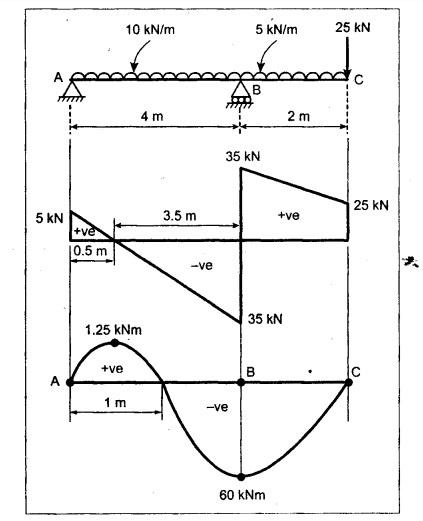
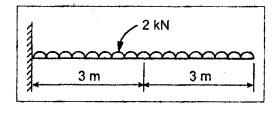
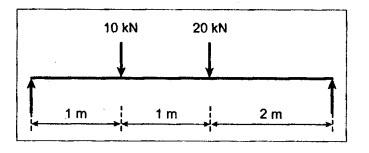
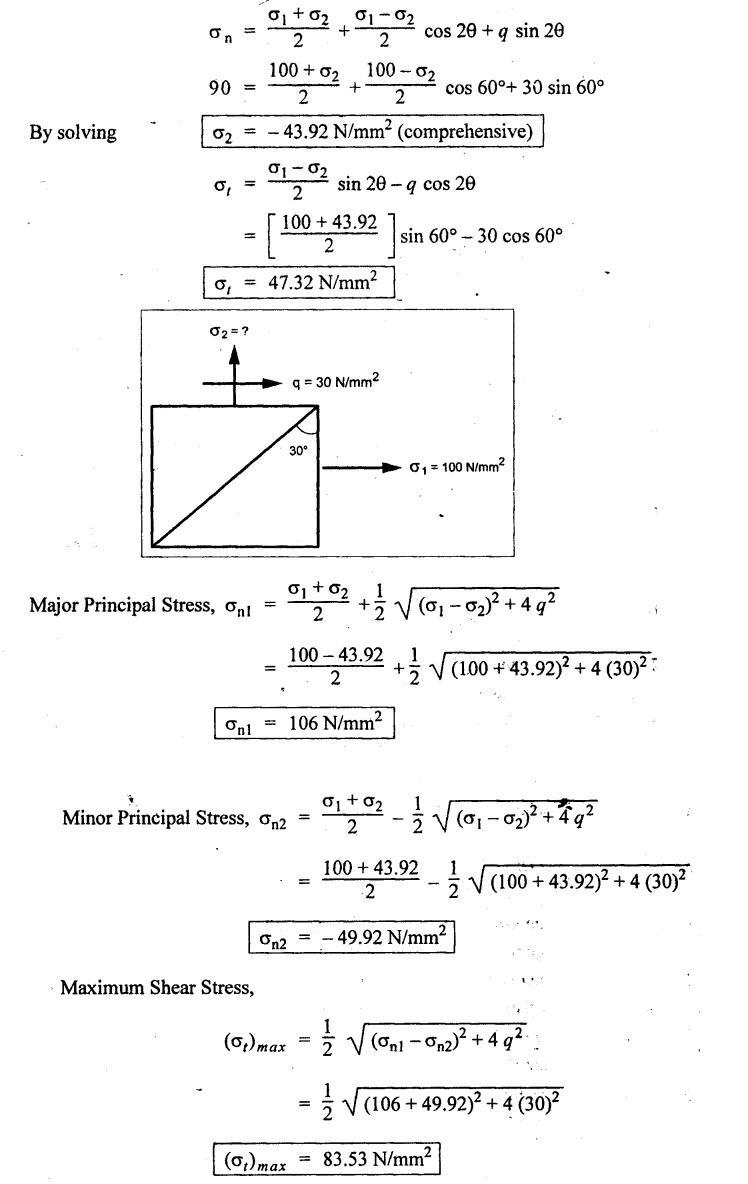
B.E./B.TECH. DEGREE EXAMINATION, NOVEMBER/DECEMBER 2008 Fourth Semester - Automobile Engineering CE1262 STRENGTH OF MATERIALS (Common to Mechanical Engineering/Mechatronics Engineering/Metallurgical Engineering/Production Engineering) (Regulation 2004) Time: Three hours Answer ALL Questions. Maximum: 100 Marks Part A (10 x 2 = 20 marks) 1. The strain induced in an MS bar of rectangular section having width equal to twice the depth is 2.5 × 10-5. The bar is subjected to a tensile load of 4 kN. Find the section dimensions of the bar. Take E = 0.2 × 106 N/mm2. Given: To find: 1. Breadth, b 2. Depth, d Solution: We know that, Result: 1. Breadth, b = 40 mm 2. Depth, d = 20 mm 2. Define Proof Resilience and Modulus of Resilience. Ans. Refer Page no. 4.103 & 4.104, Section 4.2.2 and 4.2.3. 3. Draw the shear force and bending moment diagram for a cantilever of span 4 m carrying a uniformly distributed load of 2 kN/m over the entire span. 4. A rectangular beam 150 mm wide and 200 mm deep is subjected to a shear force of 40 kN. Determine the average shear stress and maximum shear stress. 5. What is the maximum shear stress produced in a bolt of diameter 20 mm when it is tightened by a spanner which exerts a force of 50 N with a radius of action of 150 mm? Solution: 6. A close coiled helical spring of 10 mm in diameter having 10 complete turns, with mean diameter 120 mm is subjected to an axial load of 200 N. Determine the maximum shear stress and stiffness of the spring. Take G = 9 × 104 N/mm2. Given: Solution: State the expression for slope and deflection at the free end of a cantilever beam of length 'L' subjected to a uniformly distributed load of 'w' per unit length. Ans. 8. Define equivalent length of column and slenderness ratio. NOT IN SYLLABUS 9. A storage tank of internal diameter 280 mm is subjected to an internal pressure of 2.5 MPa. Find the thickness of the tank, if the loop and longitudinal stresses are 75 MPa and 45 MPa respectively. Given: Hoop stress, σc = 75 MPa Longitudinal stress, σd = 45 MPa Diameter, d = 280 mm Pressure, p = 2.5 MPa Solution: Hoop stress is greater than longitudinal stress. So we can use, 10. Define principal planes and principal stresses. Ans. Refer Page no. 1.192, Question no. 1. Part B - (5 x 16 = 80 Marks) 11. (a) (i) An aluminium cylinder of diameter 60 mm located inside a steel cylinder of internal diameter 60 mm and wall thickness 15 mm. The assembly is subjected to a compressive force of 200 kN. What are the forces carried and stresses developed in steel and aluminium? Take modulus of elasticity for steel as 200 GPa and aluminium as 50 GPa. Given: To find: Solution: We know that, We know that, Change in length of steel rod = Change in length of aluminium rod Stress in aluminium cylinder, Result: 11. (a) (ii) A rod is 3 m long at temperature of 15°C. Find the expansion of the rod, when the temperature is raised to 95°C. If this expansion is prevented, find the stress in the material of the rod. Take E = 1 × 105 N/mm2 and α = 1.2 × 10-5 per degree C. Ans. Refer Page no. 1.53, Example 1.31. [OR] 11. (b) (i) The modulus of rigidity of a material is 38 kN/mm2. A 10 mm diameter rod of the material is subjected to an axial tensile force of 5 kN and the change in its diameter is observed to be 0.002 mm. Calculate the Poisson's ratio, modulus of elasticity and bulk modulus of the material.. Ans. Refer Page no. 1.85, Example 1.41. 11. (b) (ii) The maximum instantaneous extension produced by an unknown falling weight through a height of 40 mm in a vertical bar of length 3 m and cross-sectional area of 500 mm2 is 2.1 mm. Determine the instantaneous stress induced in the vertical bar and the value of unknown weight. Take E= 2 × 105 N/mm2. Given: Height, h = 40 mm Length, l = 3 m = 3000 mm Area, A = 500 mm2 Change in length, δL = 2.1 mm Young's Modulus, E = 2 × 105 N/mm2 To find: (i) Instantaneous stress, σ (ii) Unknown load, P Solution: We know that, Substitute σ value in equation (1) Result: (i) σ = 140 N/mm2 (ii) P = 1.746 × 103 12. (a) Draw the shear force and bending moment diagram of the beam loaded as shown in Fig. Also determine the point of contraflexure if any. Solution: RA = 5 kN RB = 70 kN Point of contraflexure is Im from point A. [OR] 12. (b) (i) What do you mean by theory of simple bending? State the assumptions made in the theory of simple bending. Ans. Refer Section 2.2.1 and 2.2.2. (Page no. 2.129) (ii) A beam of rectangular cross-section 50 mm wide and 150 mm deep is used as cantilever 6 m long and subjected to a uniformly distributed load of 2 kN/m over the entire length. Determine the bending stress at 50 mm from the top fibre, at the mid-span of the beam. Also, calculate the maximum bending stress. Solution: 13. (a) (i) What do you mean by the strength of the shaft? Compare the strength (4) of solid and hollow circular shafts. Strength of the shaft: Maximum power the shaft can transmit is known as strength of the shaft. Hollow shaft is more economical than solid shaft in transmitting the same power. 13. (a) (ii) Find the diameter of a solid shaft to transit 90 kW at 160 rpm, such that the shear stress is limited to 60 N/mm2. The maximum torque is likely to exceed the mean torque by 20%. Also find the permissible length of the shaft, if the twist is not to exceed 1 degree over the entire length. Take rigidity modulus as 0.8 × 105 N/mm2. Ans. Refer Page no. 3.28, Example 3.20. [OR] 13. (b) A close-coiled helical spring is to have a stiffness of 1 kN/m of compression under a maximum load of 45 N and maximum shearing stress of 126 MPa. The solid length of the spring (i.e., when the coils are touching) is to be 45 mm. Find the diameter of the wire and mean diameter of the coil required. Take G = 42 × 103 N/mm2. Given: Stiffness, K = 1 kN/m = 1 × 103 N/m K = 1 N/mm Load, W = 45 N Maximum Shearing Stress, τ = 126 MPa = 126 N/mm2 Solid length, nd = 45 mm Modulus of rigidity, C = 42 × 103 N/mm2 Solution: nd = 45 Result: 1. Diameter of the wire, d = 3.06 mm 2. Mean diameter of the coil, D = 15.77mm 14. (a) A simply supported beam is loaded as shown in Fig. is 200 mm wide and 400 mm deep. Find the slopes at the supports, deflections under loads and location and magnitude of the maximum deflection. Take E = 2 × 104 N/mm2. Solution: Reactions at supports: RA = 17.5 kN RB = 12.5 kN Applying the boundary conditions Substituting C1 value in sloping equation. Substituting C1, C2 value in deflection equation, Slope at supports: At A, x = 0 Substitute x = 0 in equation (3) [OR] 14. (b) (i) Write the expressions for Euler's critical load of long columns for different end conditions. NOT IN SYLLABUS 14. (b) (ii) A hollow cylindrical column of 150 mm external diameter and 15 mm thick, 3 m long is hinged at one end and fixed at the other end. Find the ratio of Euler and Rankine's critical load. Take E = 8 × 104 N/mm2, fc = 550 N/mm2 and Rankine's constant as 1/1600. NOT IN SYLLABUS 15. (a) A cylindrical shell, 3 m long, which is closed at the ends, has an internal diameter of 1 m and a wall thickness of 15 mm. Calculate the circumferential and longitudinal stresses. And find the changes in dimensions of the shell, if it is subjected to an internal pressure of 1.5 MPa. Take E = 200 GPa and 1/m = 0.3. Ans. Refer Page no. 5.13, Example 5.8. [OR] 15. (b) At a point in a strained material, there is a horizontal tensile stress of 100 N/mm2 and an unknown vertical stress. There is also a shear stress of 30 N/mm2 on these planes. On a plane inclined at 30° to the vertical, the normal stress is found to be 90 N/mm2 tensile. Find the unknown vertical stress and also the principle stresses and maximum shear stress. Solution: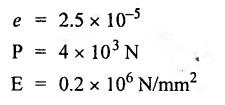

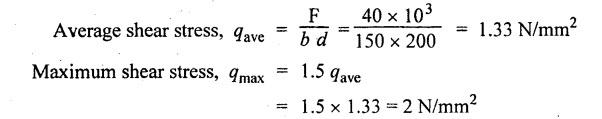
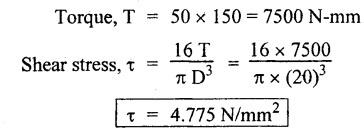


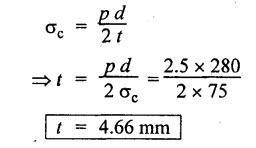

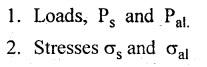
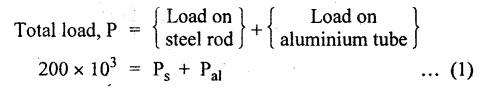

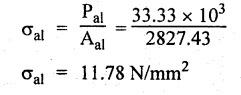
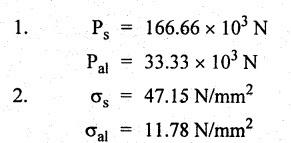
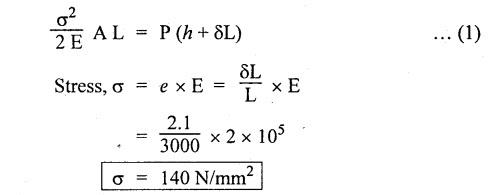
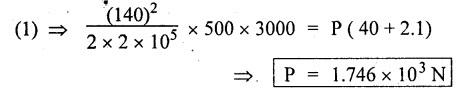


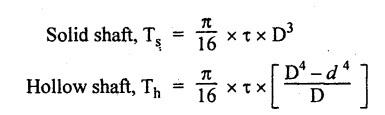


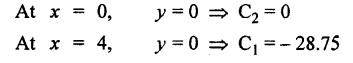
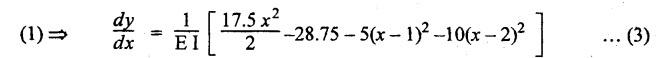
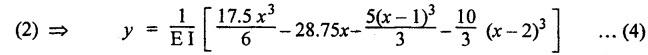

Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E./B.Tech. degree examination, november/december 2008
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
