Strength of Materials: Model Questions Papers
B.E / B.Tech. degree examinations, april / may 2022
Model Questions Papers - Strength of Materials
B.E / B.Tech. degree examinations, april / may 2022: Strength of Materials: Model Questions Papers
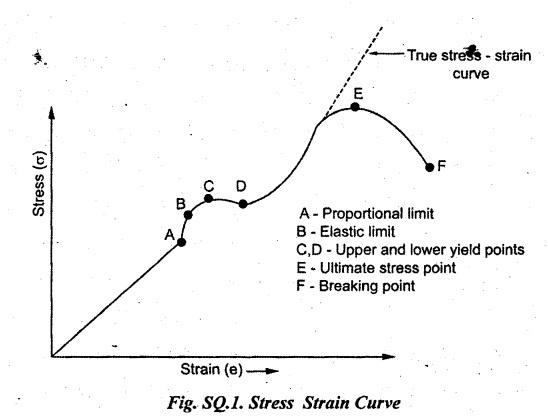
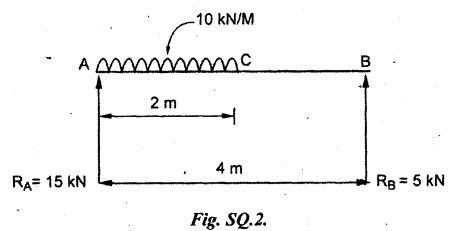
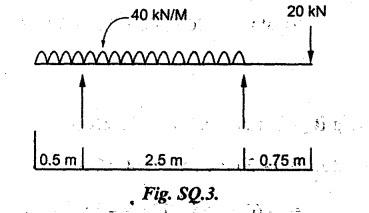
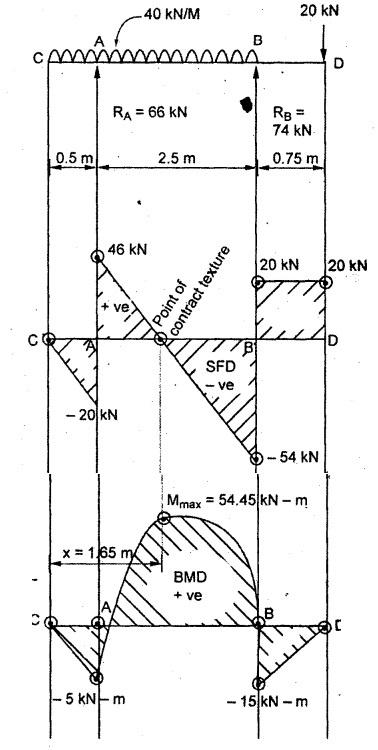
B.E / B.Tech. DEGREE EXAMINATIONS, APRIL / MAY 2022 Third Fourth Semester, Aeronautical Engineering Strength of Materials for Mechanical Engineers (Common to Aerospace Engineering / Automobile Engineering / Industrial Engineering/Industrial Engineering and Management / Manufacturing Engineering / Marine Engineering / Material Science and Engineering / Mechanical Engineering (Sandwish) / Mechanical and Automation Engineering / Mechatronics Engineering/Production Engineering / Robotics and Automation / Safety and Fire Engineering) Time: Three Hours (Regulations 2017) Answer ALL Questions Part A-(10 x 2 = 20 Marks) Maximum: 100 Marks 1. A circular steel wire is subjected to a pull of 5 kN. if the ultimate tensile stress is 250 mPa, find the minimum diameter of the wire Adopt a factor of safety of 2.5. Given: To Find: Minimum diameter d = ? Solution: d = 7.97 mm Minimum diameter d = 7.97 mm 2. A point in a stressed material is subjected to pure shear stress of 40 MPa. Find the major and minor principal stresses. Pure shear of an element means there are normal forces acting on any faces of that element. Hence the principal stresses on that element are zero. This can be visualized using Mohr's cycle where pure shear indicates the point to lie on shear axis (Y=40) where normal force (on X-axis) is zero. 3. A cantilever of length 'l' is subjected to a point load of 'W' at its free end. Draw the bending moment diagram. Ans: Refer Fig 2.6 (Bending moment diagram) Page No. 2.9 4. A mild steel strap 60 mm wide and 10 mm thick is bend into a circular arc of radius 20 m. Find the maximum bending stress induced if young's Modulus is 200 GPa. Ans: Refer Example 2.51 Page No. 2.137 5. Draw the diagram showing the shear stress distribution. Ans: Refer Section No. 3.1.5 Page No. 3.4 6. Why is a hollow shaft preferred over a solid shaft for transmitting power? Ans: Question No. 8 Page No. 3.87. 7. What is the advantage of Macaulay's method over double integration method. • In double integration method for finding slope and deflection for a simply supported beam loaded with many point loads and UDL is very tedious and laborious • In Macaulay's method integrating the continuous expression for bending moment in such a way that the constants of integration are valid for all sections of the beam. 8. Find by moment-area method the maximum slope and deflection in a prismatic cantilever of length 'l' subjected to a point load 'W' at the free end. Take flexural rigidity as EI. Ans: Refer Section No. 4.1.16 Page No. 4.32 9. Find the shear stress in a thin cylinder in terms of hoop stress and longitudinal stress. Maximum shear stress in a thin cylinder in terms of hoop stress and longitudinal stress. σ - Hoop Stress σ2 -Longitudinal stress 10. A seamless pipe of diameter Im is to carry a fluid under a pressure of 2.5 MPa. Calculate the minimum thickness of the metal if the maximum stress is not to exceed 80 MPa. Ans: Refer Page No. SQ.17 Solved Anna University Question Paper Nov/Dec 2006. PART B-(5 x 13 = 65 Marks) 11. (a) A metallic rod of diameter 10mm, when tested under an axial pull of 10kN was found to reduce its diameter by 0.003 mm. The modulus of rigidity for the material of the rod is 51 GPa. Find the Poisson's ratio, modulus of elasticity and bulk modulus. Ans: Refer Question No. 1.51 Page No. 1.101 Solved Anna University Problems [OR] (b) (i) Draw typical stress strain curve for a mild steel bar subjected to tension test marking the salient points. (ii) A reinforced concrete column is 300 mm × 300 mm in section. It carries a load of 100kN and is reinforced with steel bars of total area 2500 mm2. Calculate the stresses in concrete and steel. If the stress in concrete is not to exceed 4 MPa, find the area of steel required so that the column may support a load of 500 kN. Take modular ratio as 18. Given: To Find: (i) Stress in concrete and steel σc, σs = ? (ii) Area of steel required so that the column may support a load of 500 kN. Solutions The maximum stress in the concrete less than 4 MPa (ii) Area of steel required, so that the column may carry a load of 500 KN Result (i) Stress in concrete σc = 0.75 N/mm2 (or) 0.75 MPa Stress in steel σs = 13.58 N/mm2 (ii) Area of steel as a column may support a load of 500 kN = 2058.8 mm2 12. (a) A simply supported beam of span 5 m carries a uniformly distributed load of 10 kN/m over the entire span and also a point load of 10 kN at 2 m from the left support. If the permissible bending stress is 8 MPa, design a suitable rectangular section taking the depth twice the width. Ans: Refer Question No. 2.67 Page No. 2.162 [OR] (b) (i) State the assumptions made in theory of simple bending. Ans: Refer Section 2.2.2 Page No. 2.129 (ii) Derive bending formula. Ans: Refer Section 2.2.3 Page No. 2.130 13. (a) A hollow shaft of diameter ratio 3/5 is required to transmit 400 kW at 120 rpm the maximum torque being 30% greater than the mean. The shear stress is not to exceed 50 MPa and the twist in a length of 4 m is not to exceed 1.6°. Calculate the maximum external diameter satisfying these conditions. Take shear modulus as 80 GPa. Ans: Refer Question No. 3.27 Page No. 3.37 [OR] (b) A carriage spring 1m long is made up with steel plates width equal to six times, the thickness. Design the spring for a load of 15 kN such that the bending stress does not exceed 160 MPa and the deflection does not exceed 16 mm. Take modulus of elasticity as 200 GPa. Given: Carriage Spring Length l = 1m = 1 × 103 mm Width b = 6 t Load W = 15 kN = 15 × 103 N Bending stress. σb = 160 MPa = 160 × 103 N/mm2 Deflection δ = 16 mm Modulus of elasticity E = 200 GPa To Find: Design the spring Solution: We know that bending stress equation for semi elliptical spring. By dividing equation (2) and (1) we get Substitute t value in equation (1) we get Result: (a) Thickness of the plate t = 12.50 mm (b) Width of the plate b = 75 mm (c) No. of plates n = 12 nos 14. (a) A simply supported beam of span 4 m supported at A and B has C as the middle point. It is subjected to uniformly distributed load of 10 kN/m on the portion AC. Find the maximum deflection in terms of EI. Given: To Find: Maximum deflection in terms of EI Solution: Taking moment about A Integrating the above equation.twice Applying the following boundary conditions (i) When x = 0 y = 0 (ii) When x = 4 y = 0 Applying first boundary conditions x = 0, y = 0 in EI y equation We get C2 = 6.66 Applying second boundary conditions x = 4, y = 0 in EI y equation We choose x = 1.53 m lies between A and C maximum BM we, get maximum deflection in terms of EI Result: [OR] (b) A simply supported reinforced concrete beam of length 3.5 m is carrying a uniformly distributed load of 10 kN/m over the entire span. If the bending stress is limited to 7 MPa and deflection is not to be more than 10 mm. Find the required width and depth of the beam. Assume the depth to be twice the width. Given: Length l = 3.5 m Udl W = 10 kN/m bending stress σb = 7 MPa = 7 N/mm2 Maximum deflection δ = 10 mm d = 2b To Find: (i) Width of the beam (b) = ? (ii) Depth of the beam (ɗ) = ? Solution: Beam is simply supported (SSB) The maximum bending moment is given by By using relation For simply supported beam Deflection due to load at the centre of the beam is given by Result (i) Depth of the beam d = 297.17 mm (ii) Width of the beam b = 148.5 mm 15. (a) A cylindrical shell 3.25 m long 1m in diameter is subjected to an internal pressure of 1 MPa. if the thickness of the shell is 10 mm, find the circumferential and longitudinal stresses. Also find the maximum shear stress and change in the dimensions of the shell. Take modulus of elasticity and Poisson's ratio as 200 and 0.3 respectively. Ans: Refer Question No. 5.10 Page No. 5.16 [OR] (b) Compare the maximum tensile stress and volumetric strain of a thin cylinder and a thin spherical shell having the same internal pressure and the diameter/thickness ratio. Take Poisson's ratio as 0.3. Given: Poisson's ratio 1/m = 0.3. Solution: Volumetric strain Spherical Shell PART C (1 × 15 = 15 Marks) 16. (a) At a point in a stresssed material in a particular direction, there is a tensile stress of 20 MPa and a shear stress of 5 MPa. In the perpendicular direction. There is a normal tensile stress of 12 MPa Locate the principal planes and find the principal stresses. Also find the maximum shear stress and the resultant stress on a plane inclined at 15° to the major principal plane. Ans: Refer Page No. SQ 67 Anna university solved Question Paper Nov/Dec 2008 Question No. 15 (b) [OR] (b) Draw the shear force and bending moment diagram for the beam shown in figure given Fig.SQ.3 indicating the values of salient points: Also locate the [points of contraflexture. Given: As shown in figure SQ.3. To Find: SFD and BMD and locate the point of contraflexure. Solution: Taking Moment about A SF Calculation BM Calculation Maximum bending moment Point of Contraflexture Point of contraflexure occur where ever the bending moment is zero consider y distance from left support. [OR] 74 - 20y = 0 20 y = 74 y = 74/20 y = 2.916 m
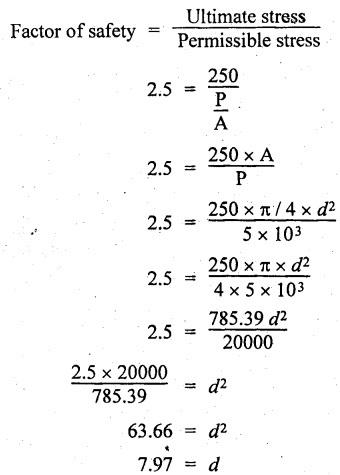
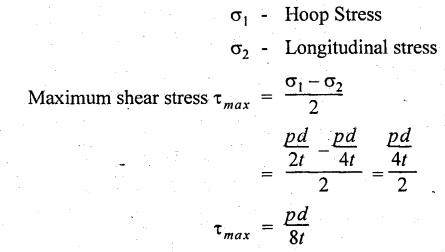


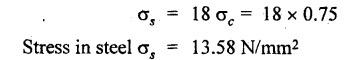

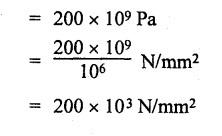

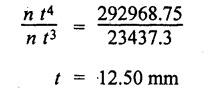
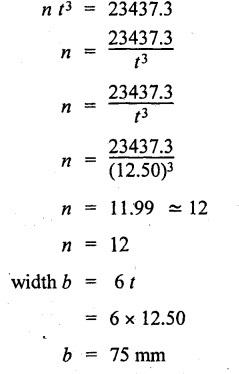

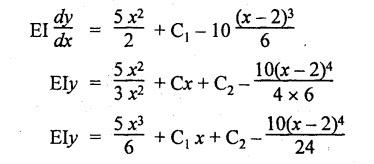
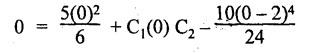


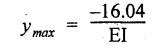

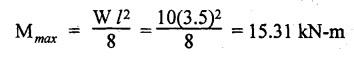




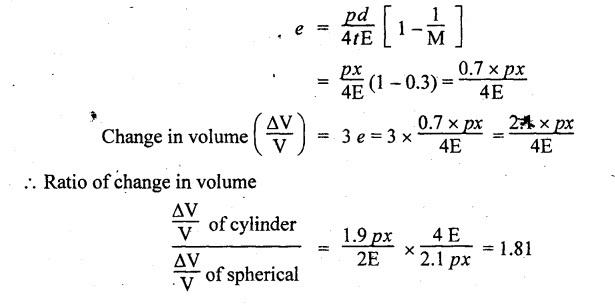
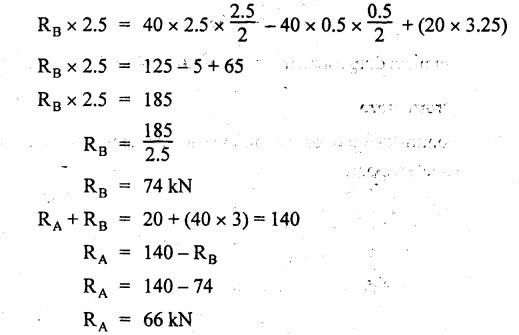
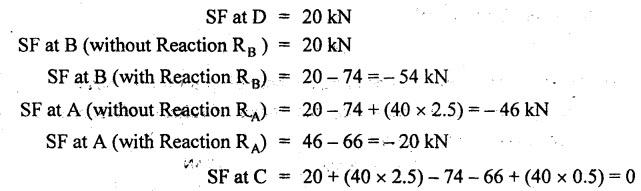
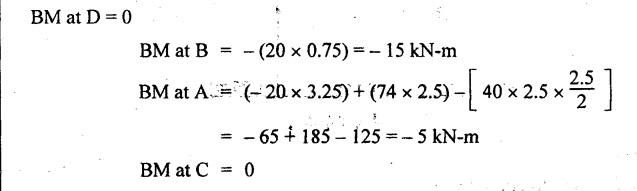
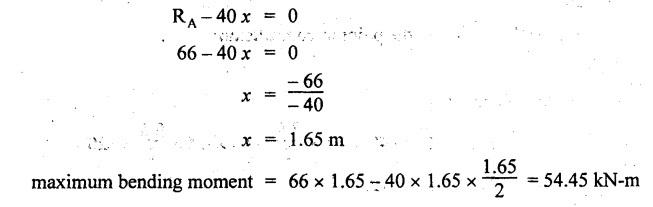
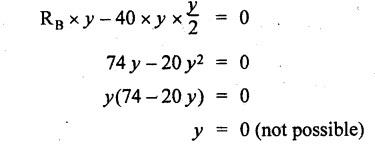
Strength of Materials: Model Questions Papers : Tag: : Model Questions Papers - Strength of Materials - B.E / B.Tech. degree examinations, april / may 2022
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
