Aronhold kennedy's theorem of three centres

ARONHOLD KENNEDY'S THEOREM OF THREE CENTRES

• Kennedy's theorem: "If three bodies have relative motion with each other, then their relative instantaneous centres must lie on a straight line.”

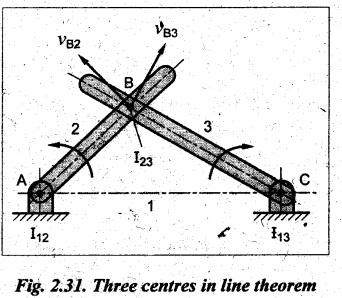
• Illustration: Fig.2.31 shows any three kinematic links having motion in one plane. The number of instantaneous centres for three links,

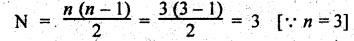
Two instantaneous centres I₁₂ and I₁₃ are permanent instantaneous centres at the pin joints A and C respectively. According to Kennedy's theorem, the third instantaneous centres I₂₃ must lie on the line joining I₁₂ and I₁₃ (not at the point A).

• Proof: Let the third instantaneous centres I₂₃ be at B, as shown in Fig.2.31. If the point I₂₃ is considered on the link 2, its velocity v_B2 has to be perpendicular to link AB. If the point I₂₃ is considered on the link 3, its velocity v_B3 has to be perpendicular to link BC. That means, the velocity y_B of instantaneous centre I₂₃ are in different directions which is impossible. Therefore the instantaneous centre of the links 2 and 3 cannot be at the assumed position of I₂₃. The velocities v_B2 and v_B3 of the instantaneous centre will be same only if this centre I₂₃ lies on the line joining I₁₂ and I₁₃.