Engineering Thermodynamics: Unit III: Availability and Applications of II Law
Applications of Second Law of Thermodynamics or Applications of Entropy Principle
Entropy principle is the quantitative approach of the second law of thermodynamics. It is due to irreversibility of the process.
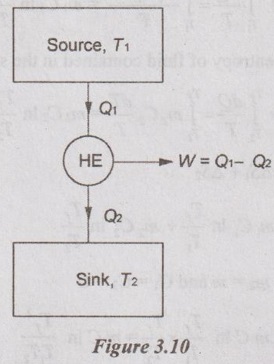
APPLICATIONS OF SECOND LAW OF THERMODYNAMICS OR APPLICATIONS OF ENTROPY PRINCIPLE Entropy principle is the quantitative approach of the second law of thermodynamics. It is due to irreversibility of the process. Entropy increases with increase in irreversibility. The following are applications of second law of thermodynamics: 1. Transfer of heat through a finite temperature difference. 2. Mixing of two fluids. 3. Maximum work obtainable from two finite bodies of temperature T1 and T2. 4. Maximum work obtainable from a finite body and thermal energy reservoir. Consider two small reservoirs of reservoir 1 at T1 and reservoir 2 at T2. It exchanges the heat (Q) from reservoir 1 to reservoir 2. For reservoir 1, the change in entropy ΔS1 = -Q /T1 [Since negative sign indicates that the heat is rejected from reservoir.] For reservoir 2, the change in entropy, ΔS2 = Q /T2 Heat transfer from reservoir 1 and reservoir 2 to the surrounding is considered as negligible. Therefore, the total entropy (or) entropy of universe is calculated by Consider a system having two subsystems as shown in Figure 3.9. Subsystem 1 contains fluid of mass m1, specific heat at constant pressure of C1 and temperature of T1 and subsystem 2 of mass m2, specific heat at constant pressure of C2 and temperature of T2. These two subsystems are separated by a partition with an adiabatic enclosure. When the partition is removed, then the two fluids will mix with each other. After the mixing is over, it will attain the thermal equilibrium of temperature Tf. Tf should always be less than T1 but it is greater than T2. By energy balance, The change in entropy of fluid contained in the subsystem 1, Similarly, the change in entropy of fluid contained in the subsystem 2, Consider two identical finite bodies containing third constant heat capacity with the same mass at the temperatures T1 and T2 respectively. Then, the final temperature is given by Tf = T1 + T2 / 2 When the heat engine is operated between these two temperatures of T1 and T2, the portion of heat (Q1) from the body 1 is supplied to the heat engine to convert into work (W). The remaining heat is rejected to the body 2. So, the temperature of body 1 decreases and simultaneously the temperature of body 2 will increase. After some time, both bodies will reach thermal equilibrium at a temperature of Tf. At thermal equilibrium temperature, the heat engine stops working. Heat supplied to heat engine, Q1 = Cp (T1 – Tf) Heat rejected to body 2, Q2 = Cp (Tf – T2) ⸫ Work delivered, W = Q1 - Q2 W = Cp (T1 - Tf - Tf + T2) = Cp (T1 + T2 - 2Tf). We know that change in entropy of body 1, Similarly, change in entropy of body 2, By entropy principle, entropy of universe, ΔSUniv1. Transfer of Heat through a Finite Temperature Difference


2. Mixing of Two Fluids




3. Maximum Work obtainable from Two Finite Bodies at Temperatures T1 and T2


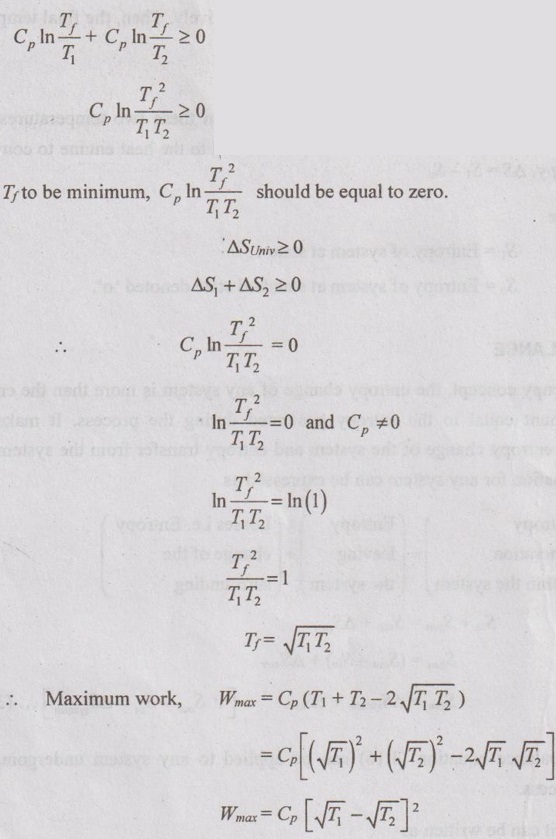
Engineering Thermodynamics: Unit III: Availability and Applications of II Law : Tag: : - Applications of Second Law of Thermodynamics or Applications of Entropy Principle
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
