Matrices and Calculus: Unit IV: Integral Calculus
Applications of Integral
Definition, Worked Examples, Exercise with Answers, Hydrostatic Force and Pressure, Moments and Centre of Mass | Integral Calculus
We can use definite integral to compute force exerted by a liquid on a surface, such as the force of water on a dam.
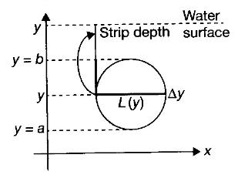
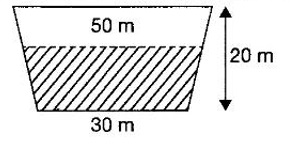
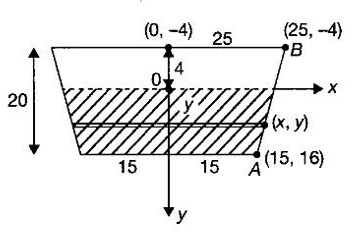
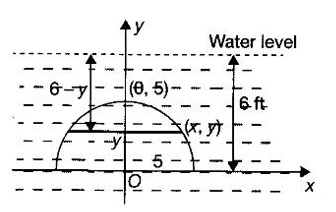
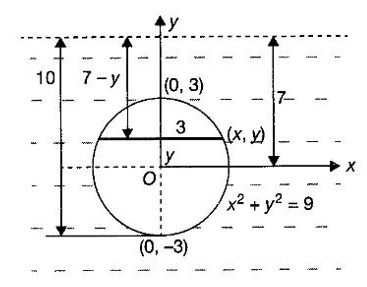
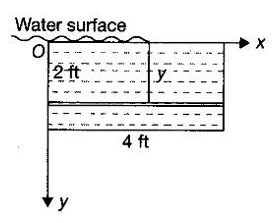
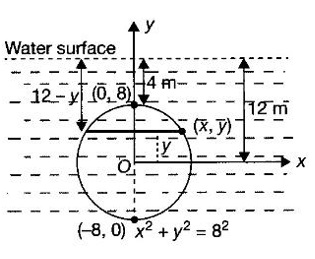
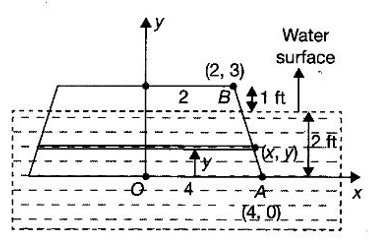
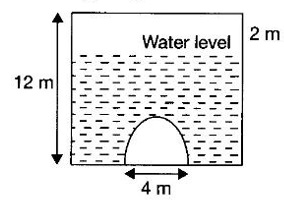
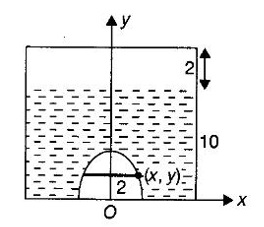
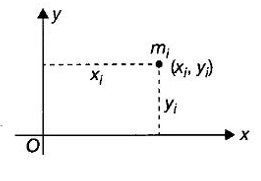
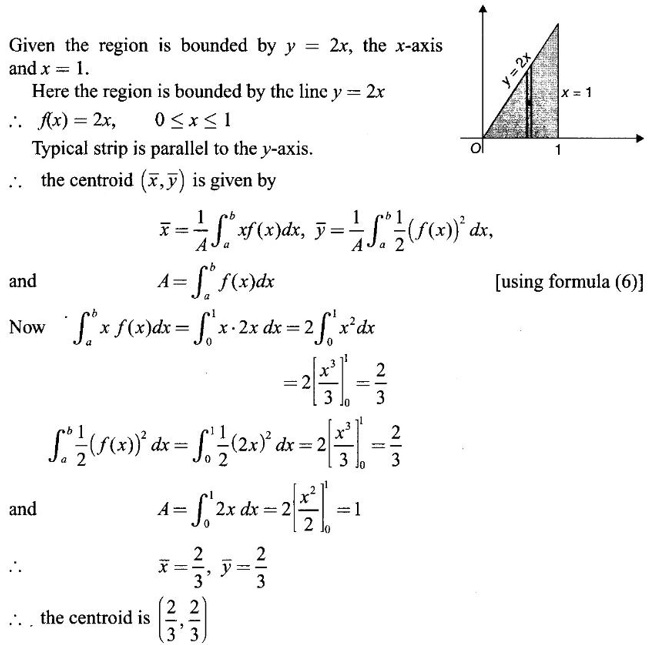
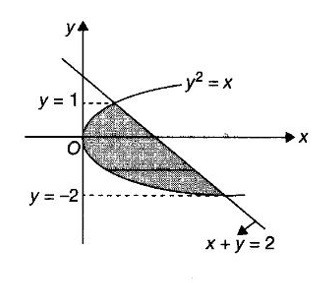
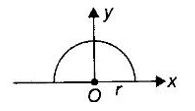
APPLICATIONS OF INTEGRAL We can use definite integral to compute force exerted by a liquid on a surface, such as the force of water on a dam. Dams are built thicker at the bottom than at the top because the pressure against them increases with depth. We need to find the force from the pressure. The pressure in a liquid is defined as the force per unit area exerted on a small piece of area in the liquid. There are two important facts about pressure (i) At any point in a liquid the pressure is same in all directions (i.e. up, down, side ways). So, a diver feels the same pressure on nose and both cars. (ii) Pressure increases with depth. This is one of the reasons why deep sea divers take extra precautions. In general, pressure P is proportional to depth d. ⸫ P = kd Definition 4.5.1 If a force of magnitude F is applied to a surface of area A, then the pressure P exerted by the force on the surface is Weight density of fresh water is δ = 62.4 lb/ft3. i.e., pounds per cubic foot in B.E system. But δ = 9810 N/m3, i.e., newtons per cubic meter in SI system. Suppose a thin horizontal plate with area A and density ρ is submerged in a fluid at a depth d below the surface. Then the fluid above the plate has volume V = Ad and its mass m = ρV = ρAd. The force exerted on the plate is F = mg =ρ gAd where g is the acceleration due to gravity This formula gives the hydrostatic force (i.e., the force exerted by a fluid at rest) against a vertical plate or wall or dam. Example Find the fluid force or hydrostatic force at the bottom of a rectangular swimming pool of size 10 ft x 20 ft containing water to a depth of 3 feet. Solution Force is given by F = δ dA Here δ = 62.4 lb/ft3, d = 3ft, A = 10 × 20 = 200 ft2 ⸫ F = (62.4 lb/ft3) × 3 ft × 200 ft2 ⇒ F = 37,440 lb 1. Integral formula for hydrostatic force against a vertical flat plate Suppose a flat plate is submerged vertically in a fluid. Pressure in the plate varies with depth. So we divide the plate into horizontal strips which may be approximately rectangles of small width so that the pressure is constant on each one. By formula (2) we find the Riemann sum for total force. Taking limit of Riemann sum we get the integral for F. Assume that the flat plate is the region in the vertical xy-plane extending from y = a to y = b. Consider a typical strip of length L(y), width Δy. Thus the element force of the strip is Forming Riemann sum and taking limit we get, Example 1 The face of a dam is a vertical rectangle of height 100 ft and width 200 ft. Find the fluid force or hydrostatic force on the face when the water surface is in level with the top of the dam. Solution Introduce the coordinate system with the left top corner as the origin and axes as shown in figure. Take a strip at a depth y depth of the strip = y L(y) = 200, δ = 62.4 = 62,400,000 lb Example 2 A flat isosceles right triangular plate with base 6 ft and height 3 ft is submerged vertically with base up and 2 ft below the surface of a swimming pool. Find the force exerted by water against one side of the plate. Solution Given an isosceles right triangle is immersed vertically in a swimming pool as in figure. Introduce the coordinate system with vertex O as the origin and the axes as in figure. Example 3 A dam had the shape of the trapezoid as in fig. the height is 20 m and width is 50 m at the top and 30 m at the bottom. Find the force on the dam due to hydrostatic pressure if the water level 4 m from the top of the dam. Solution Given the shape of a dam is a trapezoid as in figure. Introduce a coordinate system. Choose the mid point of the surface of water as the origin and water level at the x-axis and the y-axis down ward as in figure. Choose a strip parallel to the x-axis at a depth y. Here the unit of measure is meter. To find Equation of AB: Example 4 Calculate the fluid force on one side of a semicircular plate of radius 5 ft that rests vertically on its diameter at the bottom of a pool filled with water to a depth of 6 ft. Solution Given a semi circular plate of radius 5 ft is immersed in a pool with the diameter at the bottom of the pool. Choose a coordinate system with the centre as origin and the bounding diameter as the x-axis and the perpendicular radius as the y-axis as in figure. Take a strip at a height y so that the depth of the strip is 6 - y. Equation of circle is x2 + y2 = 25 Example 5 Find the hydrostatic force on one end of a cylindrical drum with radius 3 ft. If the drum is submerged in water 10 ft deep. [Given δ = 62.5 lb/ft3] Solution Given cylindrical drum with radius 3 ft is immersed in water 10 ft deep. Choose the centre of the circular face as the origin and the x-axis horizontal, y-axis vertical as in figure. Equation of the circle is x2 + y2 = 9. ⸫ Take a strip parallel to the x-axis at a distance y from O. ⸫ The depth of the strip = 7 - y Example 6 A flat rectangular plate of size 4 × 2 ft is just immersed in water with the long side horizontal. Find the fluid force against the surface of the plate. Solution Given a rectangular plate is just immersed in water with the long side horizontal. Introduce the coordinate system with left top corner of the plate as origin O and the edges as axes as in figure. Take a typical strip parallel to the x-axis at a depth y ft. Length of the strip L(y) = 4. Density δ = 62.4 lb/ft3 Example 7 A circular plate of radius 8 m is immersed in water at a depth of 4 m from the surface of water. Find the hydrostatic force on the surface of the plate [Take δ = 9800 N/m3] Solution Given a circular plate is immersed in water. Introduce a coordinate system choosing the centre of the circle as the origin O and the horizontal radius as the x-axis and y-axis perpendicular to it. The equation of the circle is Take the typical horizontal strip at a distance y from the x-axis. Then the depth of the strip = (12 - y) m Example 8 A trapezoidal plate 3 ft in height is immersed vertically in water partially with 2 ft inside water. The top of the trapezoid is 4 ft and bottom 8 ft. Find the hydrostatic force on the surface of the plate. [Take δ = 62.5 lb/ft3 ] Solution Given a trapezoidal plate is immersed partially as in figure. Introduce the coordinate system the with mid point of the bottom edge as the origin O and the bottom edge as the x-axis and perpendicular bisector of the edge as the y-axis. The corner A is (4, 0) and B is (2, 3), because the height of the trapezium is 3 ft. The depth of the strip = 2 - y, Example 9 A vertical dam has a semicircular gate as shown in figure. Find the hydrostatic force against the gate [Take δ = 9800 N/m3] Solution Given a vertical dam of height 12 m having a semicircle gate of diameter 4 m. Introduce a coordinate system with centre of the semicircle as the origin O and the bounding diameter as the x-axis and the vertical radius as the y-axis as in figure. ⸫ the equation of the circle is x2 + y2 = 22 Take the typical strip parallel to the x-axis at a distance y from x-axis. Then ⸫ the length of the strip L(y) = 2x The depth of the strip = 10 - y and δ = 9800 N/m3 ⸫ the hydrostatic force on the gate is As a physical application of integrals we consider centre of mass. Many structures and mechanical systems behave as if their masses were concentrated at a single point, called centre of mass. Here we consider masses distributed along a line or region in the plane and locating this point mathematically. Consider the simple situation of two masses m1 and m2 attached to a rod of negligible mass on opposite sides of a fulcrum at distances d1 and d2 from it. The resulting system may or may not balance. The rod will balance if 1. Masses distributed over a line 2. Masses distributed over a plane region Suppose we have n particles with masses m1, m2,… mn located at the points (x1, y1), (x2, y2),..........( xn, yn) in the xy-plane. Mx measures the tendency of the system to rotate about the x-axis. My measures the tendency of the system to rotate about the y-axis. As in one-dimension, if Example 1 If masses m1 = 12, m2 = 15, m3 = 20 are located at the points – 3, 2, 8 on the x-axis find (i) the moment of the system about the origin (ii) the centre of mass Solution Given m1 = 12, m2 = 15, m3 = 20 x1 = −3.8, x2 = 2, x3 = 8 (i) Moment of the system about the origin is = m1x1 + m2x2 + m3x3 = 12(-3) + 15 × 2 + 20 × 8 = 154 Given m1 = 12, m2 = 15, m3 = 20 and x1 = −3, x2 = 2, m3 = 8 Example 2 Find the moments and centre of mass of the system of objects that have masses 4, 2, 6 at the points (2,-3) (-3, 1), (3, 6) respectively. Solution 3. Centre of mass of a thin flat plate When the distribution of masses is continuous as in the case of a thin flat plate or disk, we use Riemann sum idea leading to an integral. Such a flat object is called a lamina. Consider a lamina with uniform density ρ we can regard the lamina as a region R in the xy-plane. Divide the region into thin strips parallel to one of the axes, say the y-axis. Let We can assume the mass Δm is concentrated at with suitable limits for the integrals. When the density ρ is a constant, the centre of a mass of the lamina is also called the centroid of the lamina. 4. Region of the plate bounded by two curves (ii) In case the strip is parallel to the x-axis, the curves are x = f(y), x = g(y) with limits y = c, y = d and f(y) ≥ g(y). Note: 1. Suppose the region is bounded by y = f(x) and the x-axis a ≤ x ≤ b. Then g(x) = 0, If the typical strip is parallel to the y-axis. 2. If the region is bounded by x = f(y) and y-axis, then g(y) = 0. If the typical strip is parallel to the x-axis with limits y = c, y = d, Example 1 Find the centroid of the region bounded by y = 2x, y = 0, x = 1 Solution Example 2 Find the centroid of the region bounded by the curves y = cos x, y = 0, x = 0 and x = π/2. Solution Example 3 Find the centre of mass of the region bounded by the parabola y = 4 - x2 and the x-axis. Solution ⸫ the centroid is (0, 1.6) Example 4 Find the centroid of the region bounded by the curves y = x2 and x = y2 Solution Given the region is bounded by Example 5 Find the centroid of the region bounded by y = 2 − x2 and y = x. Solution Given the region is bounded by y = 2 − x2 and y = x. y = 2 – x2 ⇒ x2 = 2 – y = - (y - 2), which is a parabola with vertex (0; 2) and down ward. To find the limits solve Example 6 Find the centroid of the region bounded by x = y2 and x + y = 2. Solution Given the region is bounded by two curves x = y2 and x + y = 2. Here it is convenient to take strip parallel to the x-axis. So, we find the limits for y, solve x = y2 and x + y = 2. Solving we get 2 – y = y2 ⇒ y2 + y − 2 = 0 Example 7 Find the centroid of the region bounded by the parabola y2 = 4ax, the x-axis and its latus rectum. Solution Example 8 Find the centroid of the elliptic quadrant Solution The limits are x = 0, x = a So, the typical strip is parallel to the y-axis Example 9 Find the centroid of the region bounded by the parabolas y = 2x2 - 4x and y = 2x - x2 Solution The region is bounded by the parabolas y = 2x2 - 4x and y = 2x - x2 The Equation (2) is a parabola with vertex (1, 1), the axis is x = 1 and downward So, the typical strip is parallel to the y-axis. Since both the curves are symmetric about the line x = 1, the centre of gravity will line on x = 1 1. A 3 × 4 ft rectangular plate is immersed in a pool filled with water to a depth of 10 ft. Find the fluid force (hydrostatic force) on the plate if the plate rests vertically at the bottom of the pool (i) on its 4 ft edge (ii) on its 3 ft edge. 2. A rectangular plate 8 × 2 ft is submerged in water vertically at a depth of 3 ft with the 2 ft edge a the bottom and 8 ft edge vertical. Explain how to find the hydrostatic force against one side of the plate by a Riemann sterin. Then express the force as an integral and evaluate it, (Taking δ = 62.5 lb/ft3) 3. A flat isosceles right triangular plate with base 6 ft and height 3 ft is vertically submerged with base up and 2 ft below the surface of the swimming pool. Find the force exerted by the water against one side of the plate using the coordinate system shown here in figure. 4. A trough is filled with liquid of density 840 kg/m3. The ends of the trough are equilateral triangles with sides 8 m and vertex at the bottom. Find the hydrostatic force on one end of the trough. 5. Find the moments end centre of mass of the system of objects that have masses 3, 4, 8 at the points (1, 1), (2, −1) and (2, 2) respectively. 6. Find the centre of mass or centroid of a semi-circular plate of radius r If the coordinate system is as in figure. 7. Find the centre of mass of the region bounded by y = x2 and y = 4. 8. Find the centre mass of the region bound by y = √x, y = 0, x = 4. 9. Find the centroid of the region bounded by the y-axis and the curve x = y - y3, 0 ≤ y ≤ 1. 10. Find the centroid of the region bounded by the line y = x and the parabola y = x2. 11. Find the centroid of the region bounded by the curves y = x2 and the line y = x + 6. 12. Find the centroid the region bounded by y sin x, y = cos x, x = 0, x = π/4 13. Find the centroid of the region bounded by the curves y = x - x2 and the line y = -x. 14. Find the centroid of the region bounded by the curves y = x3- x and y = x2 - 1. 1. (i) 6364.8 lb (ii) 5990.4 lb 2. 7000 lb 3. 1684.8 lb 4. 5.27 × 105 N1. Hydrostatic Force and Pressure
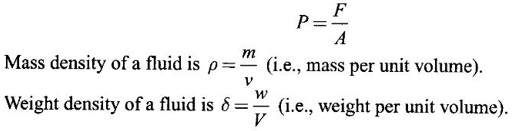
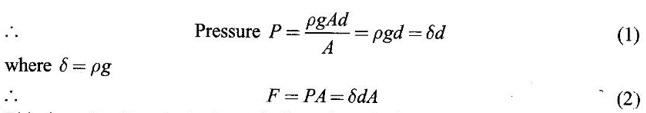
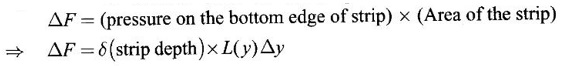
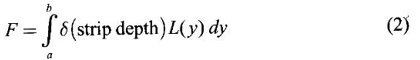
WORKED EXAMPLES






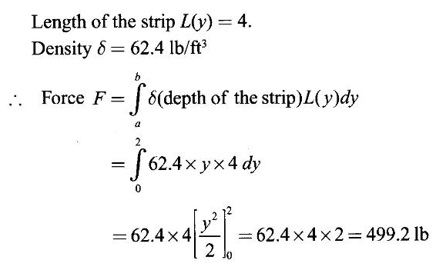
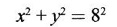

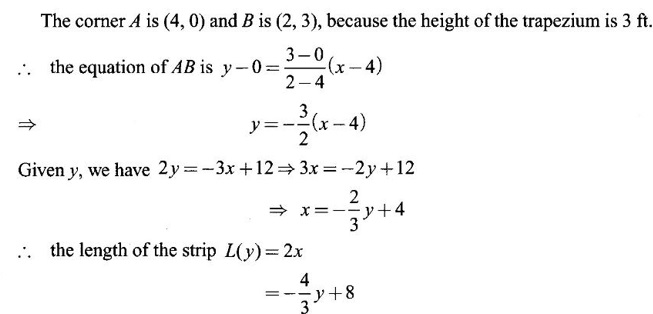
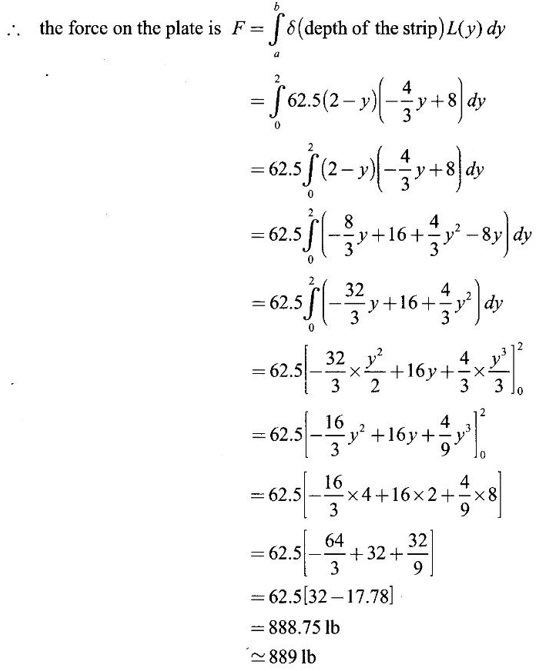
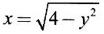
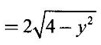

2. Moments and Centre of Mass
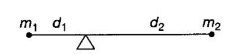
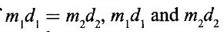 are called moments about the fulcrum of the masses m1 and m2.
are called moments about the fulcrum of the masses m1 and m2.

![]() is the centre of mass of the system, then
is the centre of mass of the system, then
WORKED EXAMPLES

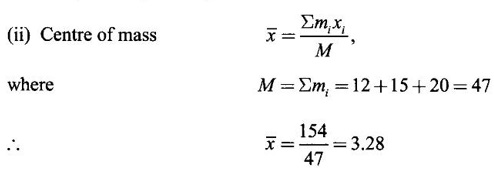

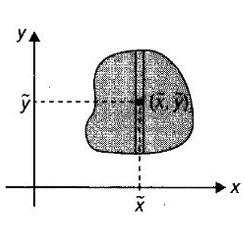
![]() be the centre of mass of a typical strip and let Δm the element mass of the strip.
be the centre of mass of a typical strip and let Δm the element mass of the strip.![]()



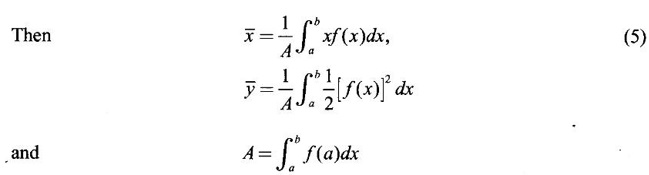
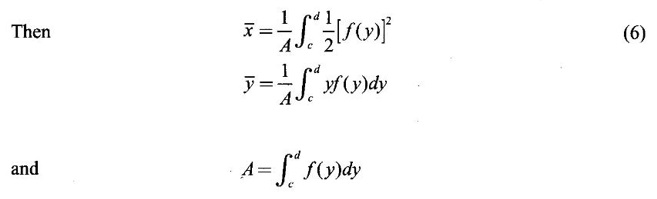
WORKED EXAMPLES


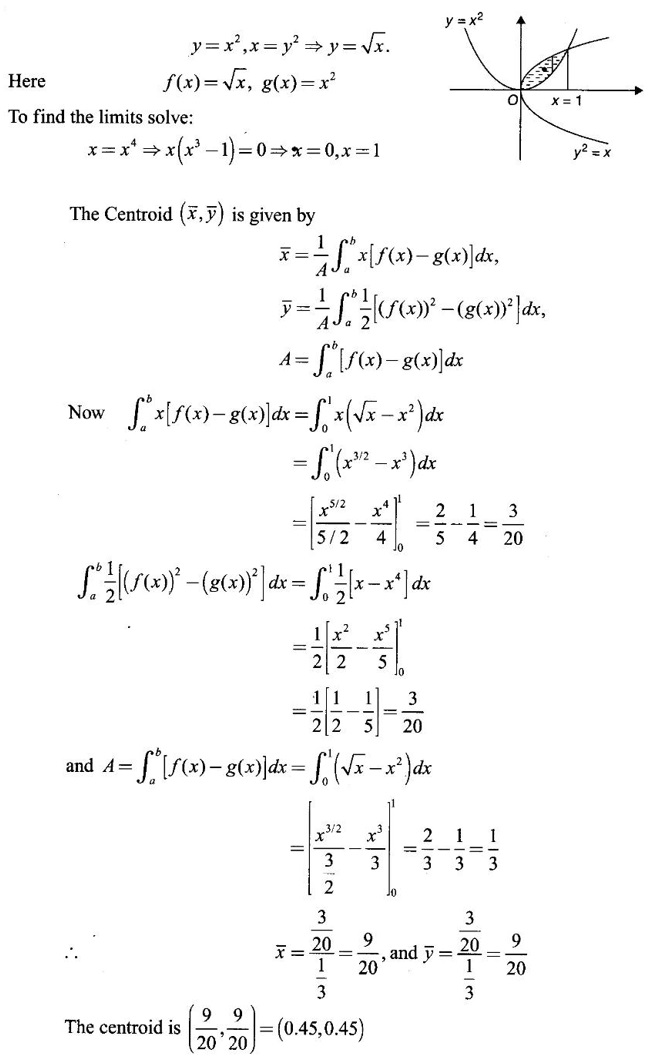
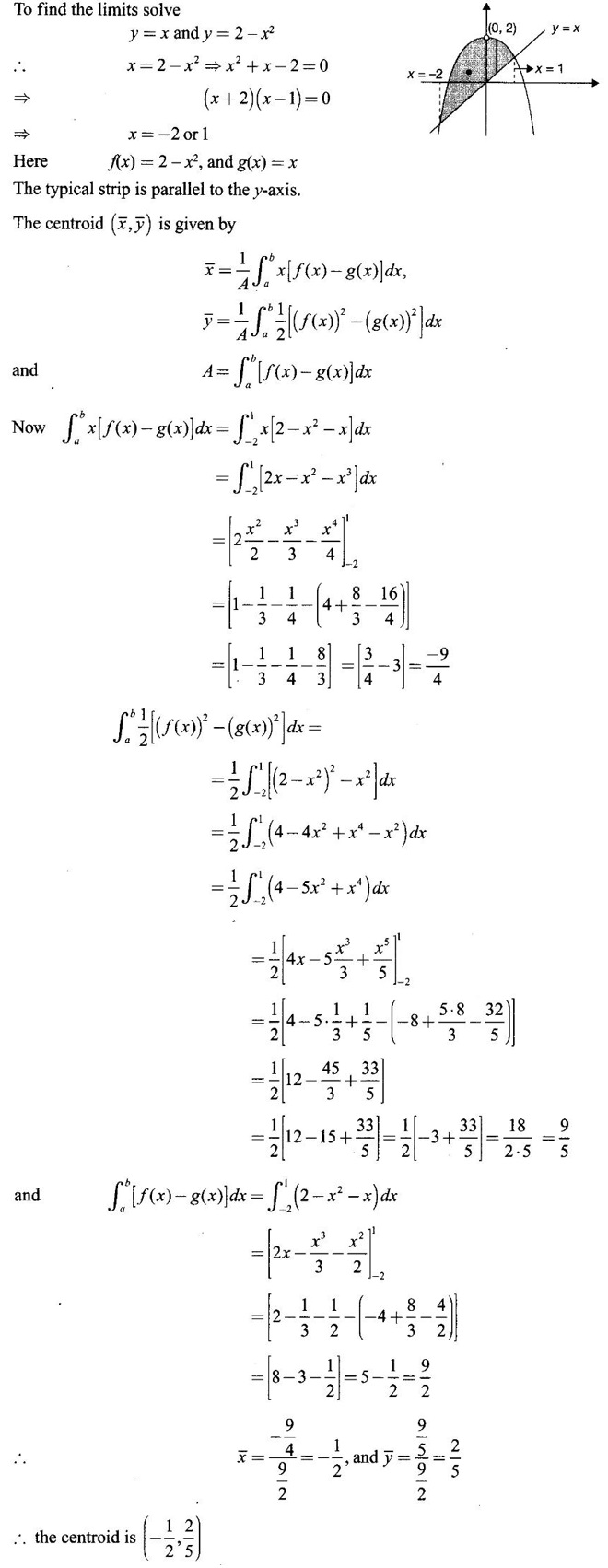
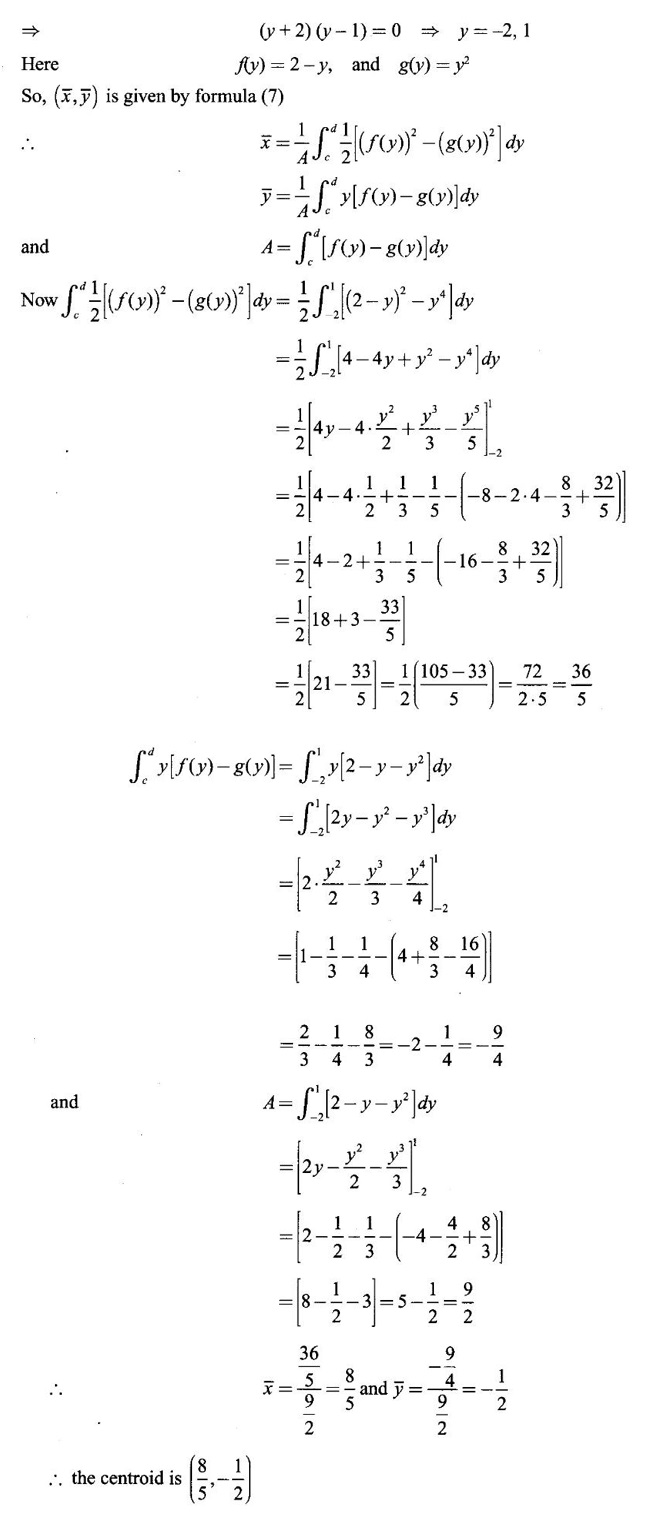

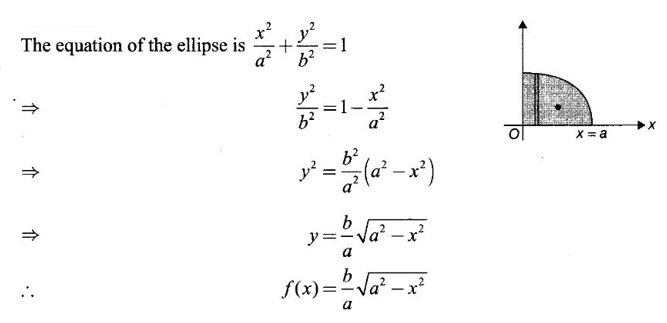
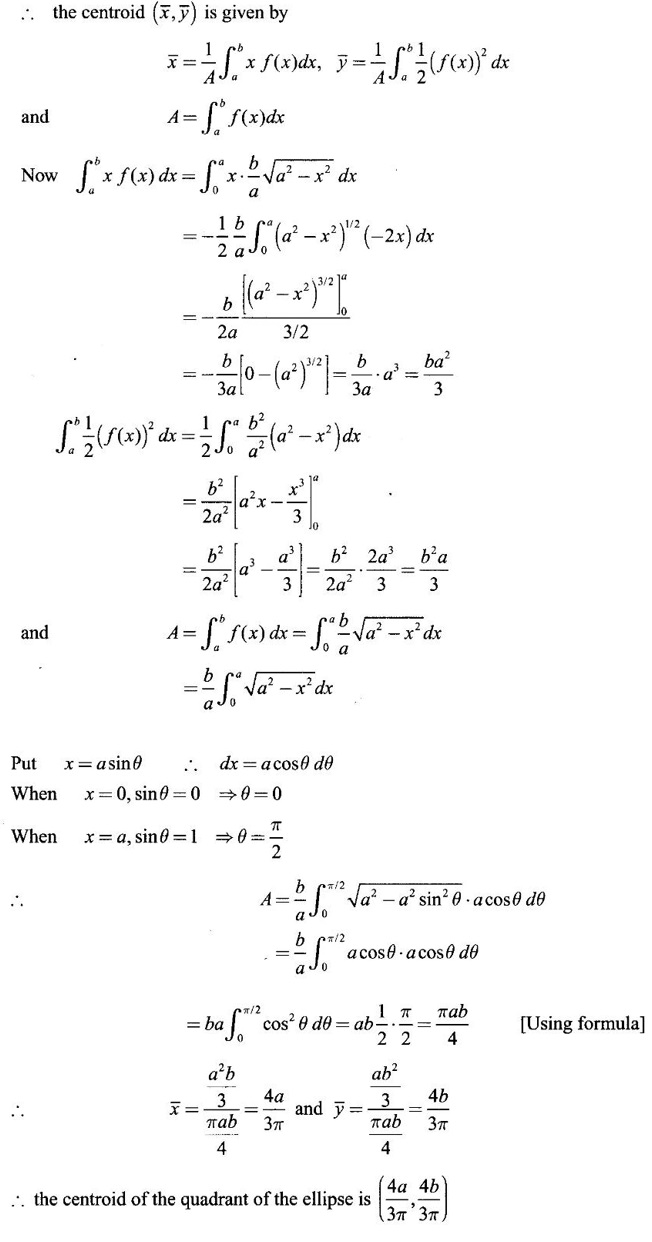
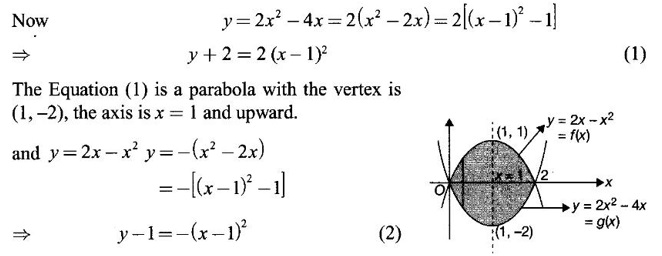
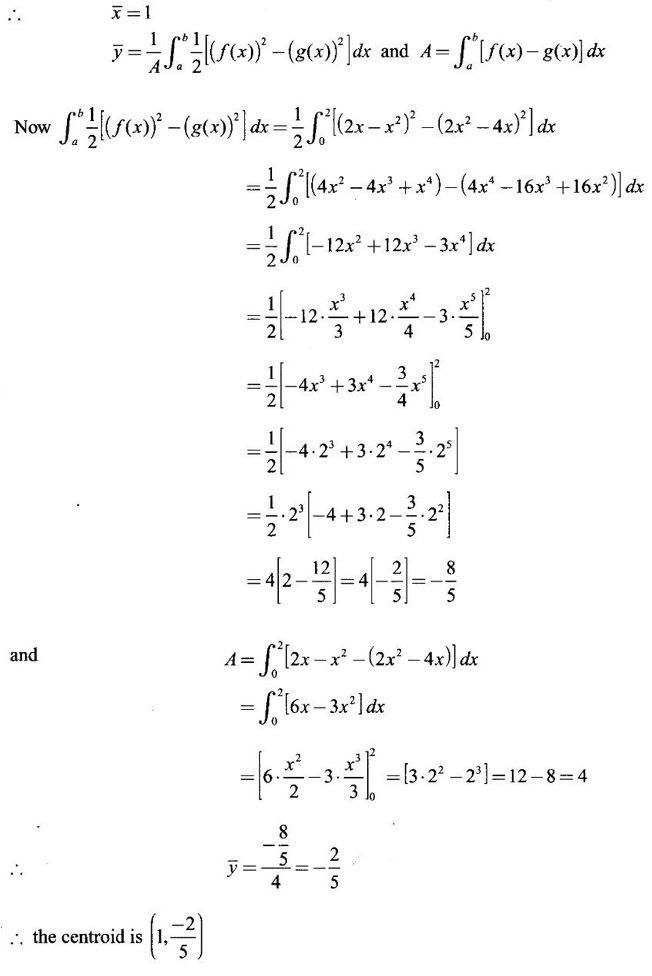
EXERCISE
ANSWERS TO EXERCISE

Matrices and Calculus: Unit IV: Integral Calculus : Tag: : Definition, Worked Examples, Exercise with Answers, Hydrostatic Force and Pressure, Moments and Centre of Mass | Integral Calculus - Applications of Integral
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
