Matrices and Calculus: Unit II: Differential Calculus
Applications: Maxima and Minima of Function of One Variable
Definition, Theorem, Worked Examples | Differential Calculus
Increasing and decreasing functions (or monotonic functions) form an important class of functions in mathematics. These functions occur in various fields
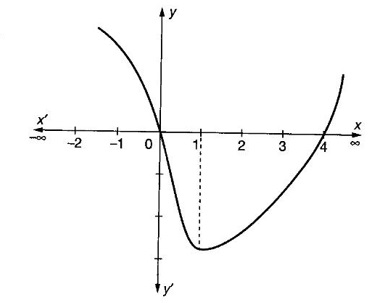
APPLICATIONS: MAXIMA AND MINIMA OF FUNCTION OF ONE VARIABLE Increasing and decreasing functions (or monotonic functions) form an important class of functions in mathematics. These functions occur in various fields Let f be a function defined in an interval I and let x1, x2 be any two points in I (i) f is increasing on I if f(x1) < ƒ(x2) whenever x1 < x2 (ii) f is decreasing on I if f(x1) > ƒ(x2) whenever x1 < x2 Note 1. It should be noted that the definitions of increasing and decreasing functions must be satisfied for every pair of points x1, x2 with x1 < x2. 2. To compare the function values, we have used strict in equality < (or >). So, it is sometimes referred to as ƒ is strictly increasing or strictly decreasing. 3. A function that is increasing or decreasing is said to be monotonic on the interval. The interval may be finite (i.e., bounded) or infinite (i.e., unbounded). Let f be a function which is continuous on the closed interval [a, b] and differentiable in the open interval (a, b) (i) If f'(x) > 0 ∀ x ∈ (a, b), then ƒ is increasing on [a, b] (ii) If ƒ'(x) < 0 ∀ x ∈ (a, b), then ƒ is decreasing on [a, b] (iii) If ƒ'(x) = 0 ∀ x ∈ (a, b), then ƒ is constant on [a, b] Example 1 Find the intervals in which f is increasing or decreasing, where f(x) = 2x3 - 9x2 - 24x + 7 Solution The critical points divide the domain (-∞, ∞) into three non-overlapping open intervals (-∞, -1), (−1, 4), (4, ∞) on which f'(x) is either positive or negative. Let us draw the graph of ƒ given by y = 2x3 - 9x2 - 24x + 7 When x = -1, f(−1) = −2 – 9 + 24 + 7 = 20 Example 2 If f(x) = x3 (x − 4), then identify the intervals on which ƒ is increasing or decreasing. Solution The critical points divide the domain (-∞, ∞) into three non-overlapping open intervals (−∞, 0), (0, 1), (1, ∞). The sign of f'(x) is either +ve or -ve in these intervals Let us draw the graph of ƒ given by y = x2/3 (x - 4) When x → 0, ƒ'(0) = -∞ ⸫ y-axis is tangent at origin Example 3 Solution Example 4 Solution 1. Increasing and Decreasing Functions
Definition 2.20

Theorem 2.10
WORKED EXAMPLES





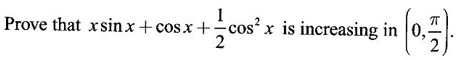

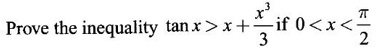

Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Theorem, Worked Examples | Differential Calculus - Applications: Maxima and Minima of Function of One Variable
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
