Matrices and Calculus: Unit III: Functions of Several Variables
Applications: Maxima and Minima for Functions of Two Variables
Definition, Worked Examples, Exercise with Answers
A common name for relative maximum or relative minimum is extreme value.
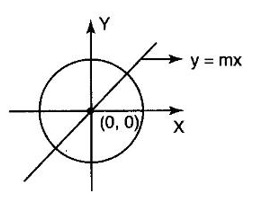
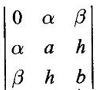
APPLICATIONS: MAXIMA AND MINIMA FOR FUNCTIONS OF TWO VARIABLES You have learned maxima and minima of a function f(x) of a single variable in x. We shall extend these ideas to a function f(x, y) of two variables in x and y. We shall derive the conditions of maxima and minima as an application of quadratic form. Definition 3.5.1 Let f(x, y) be a continuous function defined in a closed and bounded domain D of the xy-plane and let (a, b) be an interior point of D. (i) f(a, b) is said to be a local maximum or relative maximum value of f(x, y) at the point (a, b), if there exists a neighbourhood N of (a, b) such that f(x, y) < f(a, b) for all points (x, y) in N, other than the point (a, b). And, (ii) f(a, b) is said to be a local minimum or relative minimum if f(x, y) > f(a, b) for all points (x, y) in N, other than the point (a, b) Note (1) A common name for relative maximum or relative minimum is extreme value. A relative maximum or relative minimum is simply referred to as maximum or minimum. (2) In contrast, the greatest value of f(x, y) over the entire domain including the boundary is called the global maximum or the absolute maximum value of f(x, y) on D and smallest value of f(x, y) over the entire domain D is called the global minimum or absolute minimum. Definition 3.5.2 Stationary point of f(x, y) A point (a, b) satisfying ƒx = 0 and ƒy = 0 is called a stationary point of f(x, y). If f(a, b) is an extreme value of f(x, y) at (a, b), then (a, b) is a stationary point of f(x, y) if fx and fy exist at (a, b) and fx(a, b) = 0, fy (a, b) = 0 Note (1) But the converse is not true i.e., if (a, b) is a stationary point of f(x, y), then (a, b) need not be an extreme point. For example, consider the function f(x, y) defined by f(x, y) = 0 if x = 0 or y = 0 = 1 otherwise then fx(0, 0) = 0, ƒy(0, 0) = 0. But f(0, 0) is not an extreme value, i.e. (0, 0) is not an extreme point. Some more conditions are needed to ensure the extreme value. They are the sufficient conditions. (2) The graph of the function f(x, y) is the surface z = f(x, y). Corresponding to the point (a, b) in D, P (a, b, z1) where z1 = f(a, b) is a point on the surface. If (a, b) is stationary point of the function f(x, y), then P (a, b, z1) is a stationary point on the surface. If the tangent plane exists at a stationary point on the surface then it will be parallel to the xy-plane z = 0, f(a, b) is called a stationary value of f(x, y). (3) Stationary points on a surface are usually classified into three categories: maxima, minima and saddle points. If the surface is regarded as a mountain landscape we can visualise these categories as mountain tops, bottoms of valleys and mountain passe (saddle is the seat for a rider on horse back). Let (a, b) be a stationary point of the differentiable function f(x, y). i.e., ƒx (a, b) = 0, ƒy (a, b) = 0. Let ƒxx (a, b) = r, ƒxy (a, b) = s, ƒyy (a, b) = t. (i) If rt - s2 > 0 and r < 0, then f(a, b) is a maximum value. (ii) If rt - s2 > 0 and r > 0, then f(a, b) is a minimum value. (iii) If rt - s2 < 0, then f(a, b) is not an extreme value, but (a, b) is a saddle point of f(x, y). (iv) If rt - s2 = 0 then no conclusion is possible and further investigation is required. Step 1: fy = 0 as simultaneous equations in x and y. Let (a, b), (a1, b1),... be the solutions, which are stationary points of f(x, y). Step 2: Step 3: Evaluate r, s, t at each stationary point. At the stationary point (a, b) (i) If rt - s2 > 0 and r < 0, then f(a, b) is a maximum value of f(x, y). (ii) If rt - s2 > 0 and r > 0, then f(a, b) is a minimum value of f(x, y). (iii) If rt - s2 < 0, then (a, b) is a saddle point. (iv) If rt - s2 = 0, no conclusion can be made; further investigation is required. Note (i) Instead of r, s, t we can also use the symbols A, B, C respectively. (ii) The expression rt - s2 enables us to discriminate the stationary points and so it is called the discriminant of the function f(x, y). Definition 3.5.3 Critical Point A point (a, b) is a critical point of f(x, y) if ƒx = 0 and fy = 0 at (a, b) or ƒx and fy do not exist at (a, b). Maxima or minima occur at critical point. Note Generally, in this book we deal with differentiable functions f(x, y). So critical points are all stationary points. Example 1 Examine f(x, y) = x3 + y3 - 3axy for maximum and minimum values. Solution Given f(x, y) = x3 + y3 – 3axy To find stationary points, solve fx= 0 and ƒy = 0 ⸫ the stationary points are (0, 0) and (a, a) At the pont (0, 0): r = 0, s = -3a, t = 0 ⸫ rt – s2 = 0 - 9a2 < 0 ⸫ No maximum or minimum at this point. ⸫ (0, 0) is a saddle point. At the point (a, a): r = 6a, s = -3a, t = 6a If a > 0 then r > 0 and if a < 0 then r < 0 ⸫ (a, a) is a maximum point if a > 0 and is a minimum point if a > 0 Maximum value = a3 + a3 - 3a3 = -a3 if a < 0 Minimum value = -a3 if a > 0 Example 2 Examine f(x, y) = x3 + y3 - 12x − 3y + 20 for its extreme values. Solution Given f(x, y) = x3 + y3 - 12x − 3y + 20 ⸫ fx = 3x2 - 12 fy = 3y2 - 3 r = fxx = 6x s = fxy = 0 t = fyy = 6y To find the stationary points, solve fx = 0 and fy = 0 The points are (2, 1) (2, −1), (−2, 1), (−2, −1) At the point (2, 1) r = 6⸱2 = 12 > 0 s = 0 t = 6⸱1 = 6 ⸫ rt - s2 = 12 × 6 = 72 > 0 and r > 0 ⸫ (2, 1) is a minimum point. Minimum value = f(2, 1) = 23 + 1 − 12 × 2 − 3 · 1 + 20 = 8 + 1 - 24 – 3 + 20 = 2 At the point (-2, 1) r = 6 × (-2) = −12 < 0 s = 0 t = 6⸱1 = 6 ⸫ rt - s2 = 12 × 6 - 0 = −72 < 0 ⸫ (−2, 1) is a saddle point. At the point (2, −1) r = 6 ⸱ 2 = 12 > 0 s = 0 t = 6(-1) = −6 ⸫ rt - s2 = 12(−6) - 0 = −72 < 0 ⸫ (2, −1) is a saddle point. At the point (-2, -1) r = 6(-2) = -12 < 0 s = 0, t = 6(-1) = −6 ⸫ rt - s2 = (-12)(-6) - 0 = 72 > 0 and r < 0 ⸫ (-2, -1) is a maximum point. Maximum value = f(-2, -1) = (−2)3 + (−1)3 — 12(−2) — 3(-1) + 20 = -8 – 1 + 24 + 3 + 20 = 38 Example 3 Discuss the maxima and minima of f(x, y) = x3y2(1 – x – y). Solution Given We find that (0, 0) satisfies the equations (1) and (2) ⸫ we cannot say maximum or minimum. Further investigation is required. Example 4 Find the extreme values, if any, of the function f(x, y) = x4 + y2 + x2y Solution Given f(x, y) = x2 + y2 + x2y ⸫ fx = 4x3 + 2xy ƒy = 2y + x2 r = fxx = 12x2 + 2y s = fxy = 2x t = fyy = 2 To find the stationary points, solve fx = 0 and fy = 0 ⸫ 4x3 + 2xy = 0 (1) and 2y + x2 = 0 (2) ⸫ the only stationary point is (0, 0) At the point (0, 0) r = 0, s = 0, t = 2 ⸫ rt - s2 = 0 We have to investigate further. We shall study the values of the function in a neighbourhood of (0, 0). We have f(0, 0) = 0 In the neighbourhood of (0, 0) on x-axis, take the point (h, 0), ⸫ f(h, 0) = h4 > 0 On y-axis take the point (0, k), ⸫ f(0, k) = k2 > 0 On y = mx, for any m, take the point (h, mh) ⸫ f(h, mh) = m2 h2 + h2mh + h4 = h2 [m2 + mh + h2] For the quadratic in m, m2 + mh + h2 discriminant D = h2 - 4h2 = -3h2 < 0, if h ≠ 0 ⸫ m2 + mh + h2 > 0 ⸫ f(h, mh) > 0 ∀ h ≠ 0 So in the neighbourhood (0, 0) for all points (x, y) f(x, y) > ƒ(0, 0) ⸫ f(0, 0) is a relative minimum and the minimum value = 0 Example 5 Aflat circular plate is heated so that the temperature at any point (x, y) is u(x, y) = x2 + 2y2 − x. Find the coldest point on the plate. Solution Given u(x, y) = x2 + 2y2 – x ⸫ ux = 2x - 1 uy = 4y r = uxx = 2 s = uxy = 0 t = uyy = 4 To find the stationary points, solve the ƒx = 0 and ƒy = 0 ⸫ 2x – 1 = 0 and 4y = 0 r = 2, s = 0, t = 4 ⸫ rt - s2 = 2 × 4 – 0 = 8 > 0 ⸫ rt - s2 > 0 and r > 0 ⸫ So, heat is minimum at this point. So, Example 6 Find the maximum and minimum values of sin x sin y sin (x+y), 0 < x, y < π. Solution Given f(x, y) = sin x sin y sin (x + y) ⸫ fx = sin y[sin x cos(x + y) + sin(x + y)cos x] = sin ysin(x + x + y) = sin y sin(2x + y) To find the stationary points, solve ƒx = 0 and ƒy = 0 ⸫ sin y sin(2x + y) = 0 (1) and sin x sin(x + y) = 0 (2) since x, y ≠ 0 and π, sin x ≠ 0, sin y ≠ 0 ⸫ (1) ⇒ sin (2x + y) = 0 and (2) ⇒ sin (x + 2y) = 0 Since 0 < x, y < π, 0 < 2x < 2π and 0 < y < π Adding 0 < 2x + y < 3π Similarly 0 < x + 2y <3π Similarly 2x + y = 2π and x + 2y =π is also not admissible. Now take 2x + y = 2π and x + 2y = 2π Subtracting x - y = 0 ⇒ x = y ⸫ 3x - 2π ⸫ it is a minimum point. Example 7 In a plane triangle, find the maximum value of cos A cos B cos C. Solution Here A, B, C are angles of a triangle. ⸫ 0 < A, B, C < π and A + B + C = π ⸫ C = π - (A + B) ⸫ cos A cos B cos C = - cos A cos B cos (A + B) Let f(A, B) = - cos A cos B cos (A + B), 0 < A, B < π ⸫ fA = -cos B [cos A (-sin (A+B)) + cos (A+B) (−sin A)] = cos B [cos A sin (A+B) + sin A cos (A + B)] = cos B sin (2A + B) Similarly fB = cos A sin (A +2B) r = fAA = 2 cos B cos (2A + B) s = fAB = cos B cos (2A + B) + sin (2A + B)(-sin B) = cos B cos (2A + B) - sin B sin (2A + B) = cos (2A + 2B) t = fAB = 2cos A cos (A + 2B) To find the stationary points, solve fA = 0 and fB = 0 ⸫ cos B sin (2A + B) = 0 and cos A sin (A + 2B) = 0 ⸫ cos B = 0 or sin (2A+B) = 0 and cos A = 0 or sin (A + 2B) = 0 Cases In many practical problems on maxima and minima we have to find the extreme values of a function of two or more variables which are not independent but are connected by some relation. For example, suppose we want to find the maximum value of x2 + y2 + z2 (1) subject to the condition 2x + 3y + 5z = 7 (2) One method is to find z from (2) and substitute in (1), then it reduces to a function u (x, y) of two independent variables x and y. As above, we can find the maximum or minimum value of u (x, y). Suppose the relation between the variables is complicated, then finding z interms of x and y will be difficult or impossible. In such cases we use the versatile Lagrange's multiplier method, in which the introduction of a multiplier enables us to solve the constrained extreme problems without solving the constrained equation for one variable in terms of others. Lagrange's method of (undetermined) multiplier Let f(x, y, z) be the function whose extreme values are to be found subject to the restriction ø (x, y, z) = 0 (1) between the variables x, y, z. Construct the auxiliary function F(x, y, z) = f(x, y, z) + λ ø (x, y, z) where λ is an undetermined parameter independent of x, y, z. λ is called Lagrange's multiplier. Any relative extremum of f(x, y, z) subject to (1) must occur at a stationary point of F(x, y, z). The stationary points of F are given by Solving these equations, we find the values of x, y, z, which are the stationary points of F, giving the maximum and minimum values of f(x, y, z). Note This method does not specify the extreme value obtained is a maximum or minimum. It is usually decided from the physical and geometrical considerations of the problem. A method on the basis of quadratic form is given below to decide maxima or minima at the stationary point for constrained maxima and minima. We shall see sufficient conditions given by quadratic form of the differentials. 1. For unconstrained functions. Let u = f(x, y) be a function of two variables. ⸫ the total differential du = ƒx dx + ƒy dy Necessary conditions for maxima or minima of u = f(x, y) is du = 0 ⇒ ƒx dx + ƒy dy = 0 ⇒ ƒx = 0, ƒy = 0, since dx, dy may take any value. The sufficient condition for minimum is d2u > 0 and maximum is d2u < 0. Thus du = 0 and d2u > 0 are the necessary and sufficient conditions for minimum. Similarly, du = 0 and d2u < 0 are the necessary and sufficient conditions for maximum. Now, d2u = d(fx) dx + d(fy) dy Thus d2u is a quadratic form in dx, dy. The matrix of the quadratic form is called the Hessian matrix. Its principal minors are D1 = fxx = r For minimum d2u > 0 i.e., the quadratic form is positive definite. ⸫ D1 > 0, D2 > 0 ⇒ r > 0 and rt - s2 > 0 For maximum, d2u < 0 ⇒ D1 < 0, D2 > 0 ⇒ r < 0 and rt - s2 > 0 This can be extended to three or more variables. The necessary and sufficient conditions are (i) for maximum du = 0 and d2u < 0 and (ii) for minimum du = 0 and d2u > 0. 2. If u = f(x, y, z) then du = ƒx dx + fy dy + fz dz and which gives the stationary points. The matrix of the quadratic form in dx, dy, dz is the At a stationary point (a, b, c), if D1 > 0, D2 > 0, and D3 > 0, then u is minimum. If D1 < 0, D2 > 0, and D3 < 0 then u is maximum. In the same way we can extend to function of n variables f(x1, x2, ..., xn) 3. We shall now see how the Hessian changes in the discussion of constrained maxima and minima. For example, consider the quadratic form in two variables. Q = ax2 + 2hxy + by2 with linear constraint αx + βy = 0 The determinant quadratic form Q which is bordered by coefficients of the linear constraint. So, this is called a bordered determinant. Thus the corresponding matrix is called the bordered Hessian matrix. Since D1 = - α2 is always negative, Q > 0, if D2 < 0 Q < 0, if D2 > 0 4. We shall now consider quadratic form in three variables. Since D1 = b2 is always negative, Q > 0 if D2 < 0 and D3 < 0 and Q < 0 if D2 > 0 and D3 < 0. Similarly, we can discuss conditions for more than three variables. 5. Extremum with general constraints Extreme values of u = f(x, y) subject to φ (x, y) = 0 Stationary points are given by du = 0, φ = 0 At a stationary point, maximum if d2u < 0 and φ = 0 and u is minimum if d2u > 0 and dφ = 0 where d2u = fxx(dx)2 + fyy (dy)2 + 2fxy dx dy is a quadratic form in dx, dy and dφ = 0 ⇒ φx dx + φy dy = 0, which is linear in dx, dy. So, the corresponding bordered Hessian matrix 6. Extreme values of u = f(x, y, z) subject to φ (x, y, z) = 0. The bordered Hessian matrix is 7. Sufficient conditions for Lagrange's method Extreme values of f(x, y, z) subject to φ (x, y, z) = 0 Form the auxiliary function F(x, y, z) = f(x, y, z) + λ φ (x, y, z), where λ is the Lagrange's multiplier. Stationary points are given by Fx = 0, Fy = 1, Fz = 0, φ = 0 At the stationary point we have maximum if d2F < 0, dφ = 0 ⇒ φx dx + φy dy + φz dz = 0 and minimum if d2F > 0, dφ = 0 The corresponding bordered Hessian is ⸫ At a stationary point f(x, y, z) is minimum if D2 < 0 and D3 < 0 and maximum if D2 > 0 and D3 < 0 Example 1 A rectangular box, open at the top, is to have a volume of 32 cc. Find dimensions of box which requires least amount of material for its construction. Solution Let x, y, z be the length, breadth and height of the box. Given volume of the box is 32 cc. ⇒ xyz = 32, x, y, z > 0 (1); We want to minimize the amount of material for its construction. i.e.. surface area of the box is to be minimized. Surface area S = xy + 2xz + 2yz [⸪ top is open] (2) We shall solve by two methods. Method 1: xyz = 32 ⸫ x2y = xy2 Method 2: Lagrange's method We have to minimise S = xy + 2xz + 2yz (1) Subject to xyz = 32 ⇒ xyz – 32 = 0 (2) Form the auxiliary function F(x, y, z) = xy + 2xz + 2yz + λ(xyz - 32) where λ is the Lagrange's multiplier. To find stationary points, solve From (3), (4) and (5) Substituting in (2) we get ⸫ the stationary point is (4, 4, 2) So the dimensions are 4 cm, 4 cm, 2 cm. Remark We have not justified S is minimum at (4, 4, 2). We shall use the bordered Hessian to decide. Since D1 < 0, D2 < 0, D3 < 0 d2F is positive definite hence minimum. ⸫ the function S is minimum when x = 4, y = 4 and z = 2. Example 2 Find the shortest distance from the origin to the curve x2 + 8xy + 7y2 = 225. Solution Let O be the origin. Let P(x, y) be a point on the curve x2 + 8xy + 7y2 = 225. OP is minimum, if f(x, y) is minimum. ⸫ we have to minimize f(x, y) subject to where λ is the Lagrange's multiplier. To find stationary points solve ⸫ From (2) and (3) Putting 2x = y in (1), we get Thus the shortest distance - 5 Remark To decide the point giving maximum or minimum, we shall form the Since D1 < 0 and D2 < 0, f(x, y) is minimum at (+√5, +2√5) Similarly f(x, y) is minimum at (−√5,-2√5) Example 3 Find the shortest and longest distance from the point (1, 2, -1) to the sphere x2 + y2 + z2 = 24, using Lagrange's method of constrained maxima and minima. Solution Let P(x, y, z) be a point on the sphere x2 + y2 + z2 = 24 and A be (1, 2, −1). AP is minimum or maximum if f(x, y, z) is minimum or maximum. So we minimize or maximize f(x, y, z) subject to x2 + y2 + z2 = 24 Form the auxillary function where λ is the Lagrange's multiplier. To find the stationary points solve Fx = 0, Fy = 0, Fz = 0, φ = 0 We have x2 + y2 + z2 = 24 Example 4 The temperature T at any point (x, y, z) in space is T = 400 xyz2. Find the highest temperature on the surface of the unit sphere x2 + y2 + z2 = 1. Solution We want to maximize T = 400 xyz2 subject to where λ is the Lagrange's multiplier. ⸫ Fx = 400 yz2 + 2λx Fy = 400xz2 + 2λy Fz = 800xyz + 2λz To find stationary points, solve Fx = 0, Fy = 0, Fz = 0, φ = 0 From (2), (3) and (4), we get Substituting in (1) we get y2 + y2 + 2 y2 = 1 ⇒ 4 y2 = 1 These give 8 stationary points. We want the maximum value of T = 400 xyz2, and so we must have xy positive. This will occur at 4 of the points. = 50°C Example 5 Find the volume of the largest rectangular parallelopiped that can be inscribed in the ellipsoid Solution Given the ellipsoid By the symmetry of the ellipsoid, for the largest parallelopiped, the edges must be parallel to the coordinate axes and the centre coincides with the centre (0, 0, 0) of the ellipsoid. Let P(x, y, z) be the coordinates of a vertex on the ellipsiod, then the dimensions of the rectangular parallelopiped (or cuboid) are 2x, 2y, 2z respectively. ⸫ volume V = 2x · 2y · 2z = 8xyz Let We want to maximize V subject to φ (x, y, z) = 0 Form the auxiliary equation F(x, y, z) = V + λ φ (x, y, z) where λ is the Lagrange's multiplier. To find stationary points solve Fx = 0, Fy = 0, Fz = 0, φ = 0 ⸫ there are 8 stationary points. Since we want maximum value of V, choose the points with xyz positive. This will occur at 4 of the points. They are Example 6 Divide the number 24 into three parts such that the continued product of the first, square of the second and the cube of the third may be maximum. Solution Let 24 be divided into 3 parts x, y, z so that x + y + z = 24 where x, y, z > 0 ⸫ x + y + z – 24 = 0 (1) and the product is xy2 z3 We have to maximize this product subject to (1) Form the auxiliary function where λ is the Lagrange's multiplier. Substitute in (1) x + 2x + 3x = 24 ⇒ 6x = 24 ⸫ x = 4 y = 8 and z = 12 ⸫ the product is maximum if the parts are 4, 8, 12. Note We shall test it is indeed maximum. Now Fx = y2z3 + λ When x = 4, y = 8, z =12 − (− 1)27 125[1 · 12 - 4(-1 - 2)] [expanding by R3] = (− 1)27 · 125 [12 + 12] = (-1)27.125.24 = -1210.125.3 < 0 Since D1 < 0, D2 < 0 and D3 < 0, f(x, y, z) is maximum at (4, 8, 12). Example 7 Find the maximum value of xm yn zp subject to x + y + z = a Solution Let f(x, y, z) = xm yn zp (1) Maximize (1) subject to φ (x, y, z) = x + y + z – a = 0 (2) Form the auxiliary function F(x, y, z) = f(x, y, z) + λ φ (x, y, z) where λ is the Lagrange's multiplier. To find stationary points, solve Fx = 0, Fy = 0, Fz = 0, φ = 0 ⸫ From (2), (3) and (4), we get Example 8 Using Lagrange's method of multipliers, show that the stationary value of a3x2 + b3y2+ c3z2, where Solution Given f(x, y, z) = a3x2 + b3y2+ c3z2 and the constraint is Form the auxiliary function F(x, y, z) = f(x, y, z) + λø(x, y, z) where λ is the Lagrange's multiplier. To find the stationary points, solve ⸫ the stationary value occurs at the point, Example 9 If u = x2 + y2 + z2 where ax + by + cz − p = 0, then find the stationary value of u. Solution Given u = f(x, y, z) = x2 + y2 + z2 Form the auxiliary function where λ is the Lagrange's multiplier. To find stationary points, solve Substituting in (1), we get Note In this problem by geometrical consideration we can prove the stationary value is the minimum value of u. The constraint equation ax + by + cz = p is the equation of a plane. x2 + y2 + z2 is the square of the distance of any point (x, y, z) on the plane from O. The perpendicular distance from O to the plane is and it is the least value of the square of the distance of O from the plane. ⸫ the minimum value of u = Example 10 Find the minimum value of x2yz3 subject to 2x + y + 3z = a. Solution Given f(x, y, z) = x2yz3 Form the auxiliary function F(x, y, z) = f(x, y, z) + λ ø (x, y, z) where λ is the Lagrange's multiplier. F(x, y, z) = x2yz3 + λ(2x + y + 3z - a) To find stationary points, solve Fx = 0, Fy = 0, Fz = 0, ø = 0 Substituting in (1), 2x + y + 3z = a Example 11 If xyz = 8, find the values of x, y, z for which u = Solution Given u = u is maximum if x +2y + 4z is minimum. So, we minimize f(x, y, z) = x +2y + 4z Subject to ø (x, y, z) = xyz – 8 = 0 (1) Form the auxiliary function where λ is Lagrange's multiplier. To find stationary points, solve Note We shall justify by bordered Hessian. We see λ = -1/2 At the point (4, 2, 1) Fxx = 0, Fyy = 0, Fzz = 0 Bordered Hessian matrix is = 8[0(0 − 4) + 1(0 − 2) - 3(2 − 0)] = 8[−2 −6] = −64 Since D1 < 0, D2 < 0, D3 < 0, f(x, y, z) is minimum at (4, 2, 1). 1. Find the extreme values of the function f(x, y) = x3 + y3 − 3x − 12y + 20. 2. Find the maximum and minimum values of x2 - xy + y2 -2x + y. 3. Find the maximum and minimum values of x3 + 3xy2 – 15y2 + 72x 4. Find the maxima and minima of the function x3y2(12 − x − y). 5. Find the extreme values of the function 6. Find the extreme values of the function y4- x4 + 2(x2 - y2). 7. If the perimeter of a triangle is a given constant, show that the area is maximum when the triangle is equilateral. 8. Locate the stationary points of x2 + y4 − 2x2 + 4xy - 2y2 and determine their nature. 9. Examine maximum and minimum values of sinx + siny + sin (x + y), 0 < x <π, 0 < y <π. 10. Find the dimensions of the rectangular box open at the top, of maximum capacity whose surface is 432 sq.cm. 11. Find the minimum value of x2 + y2 + z2, given that xyz = a3. 12. Find the maximum and minimum distances of the point (3, 4, 12) from the sphere x2 + y2 + z2 = 1. 13. Find the maximum and minimum distances from the origin to the curve 5x2 + 6xy + 5y2 – 8 = 0. 14. Find the minimum values of the function x2 + y2 + z2 subject to the condition ax + by + cz = a + b + c 15. Find the minimum values of the function x2 + y2 + z2 subject to the condition xy + yz + zx = 3a2. 16. A thin closed rectangular box is to have one edge equal to twice the other and a constant volume 72 m3. Find the least surface area of the box. 17. Show that the area of the greatest rectangle that can be inscribed in an ellipse 4x2 + 9y2 = 36, having its sides parallel to the axes is 12 sq. units. 1. (i) Minimum at (1, 2); Minimum value = 2 (ii) Maximum at (-1, -2); Maximum value = 38 2. Minimum at (1, 0); Minimum value = −1 3. (i) Maximum at (4, 0); Maximum value = 112 (ii) Minimum at (6, 0); Minimum value = 108 4. Maximum at (6, 4); Maximum value = 6912 5. Minimum at Minimum value = 34/3 6. (i) Minimum at (0, ±1); Minimum value = -1 (ii) Maximum at (±1, 0); Maximum value = 1 8. (i) Minimum at (√2, −√2) and (−√2, √2) 9. Maximum at 10. Dimensions 12, 12, 6 cms. 11. Minimum value = 3a2 12. Maximum distance = 14, minimum 12 13. Maximum distance = 4, minimum distance = 1 14. Minimum value 15. Minimum value = 3a2 16. 108 m2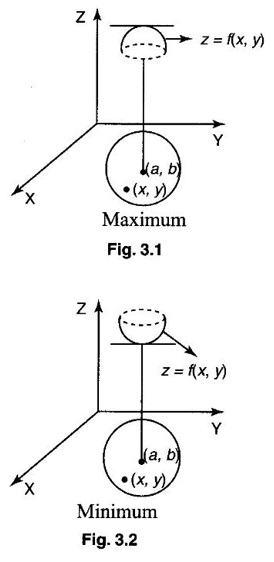
1. Necessary conditions for maximum or minimum
2. Sufficient conditions for extreme values of f(x, y).
3. Working rule to find maxima and minima of f(x, y)
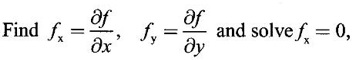
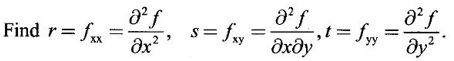
WORKED EXAMPLES
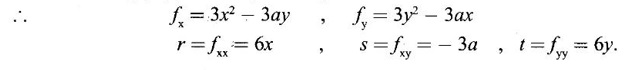

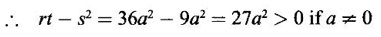
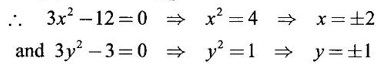




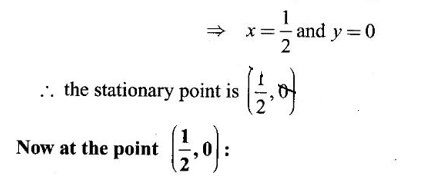
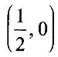 is a minimum point.
is a minimum point.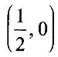 is the coldest point on the plate as it is the only critical point.
is the coldest point on the plate as it is the only critical point.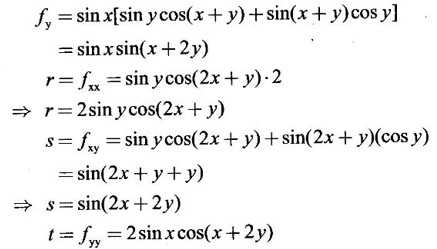


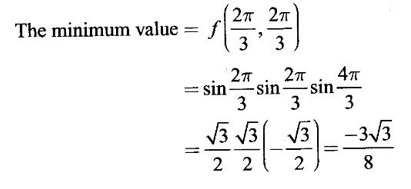


4. Constrained Maxima and Minima

5. Method to decide maxima or minima
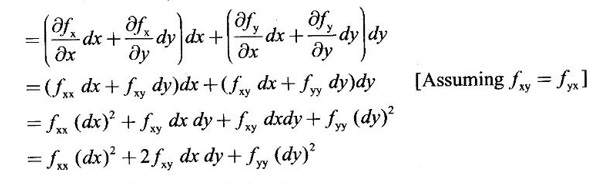
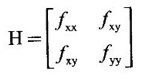
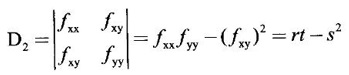
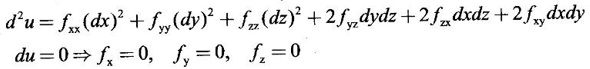
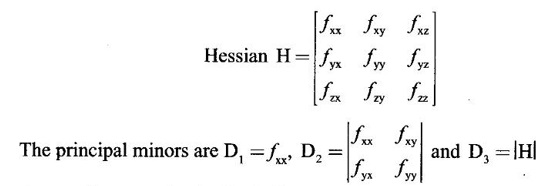
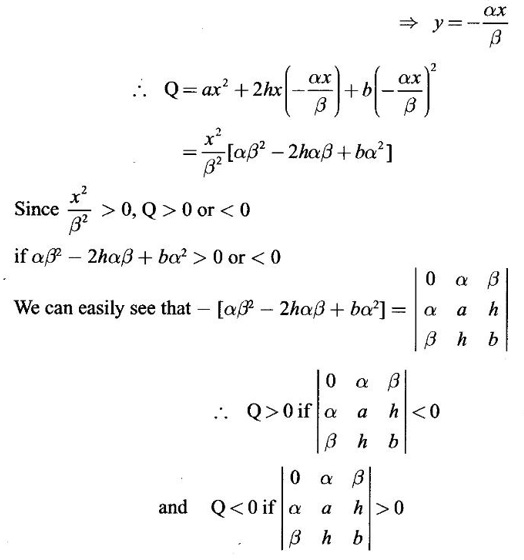
 is made up of the matrix of coefficients of the
is made up of the matrix of coefficients of the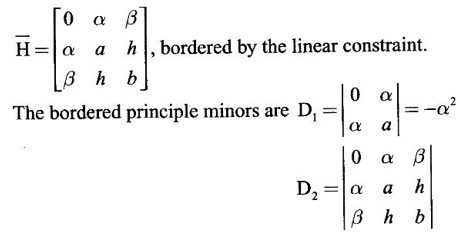



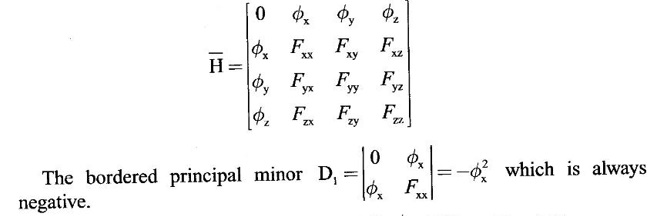
WORKED EXAMPLES


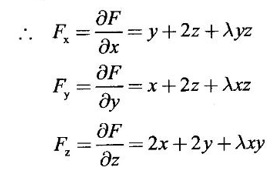

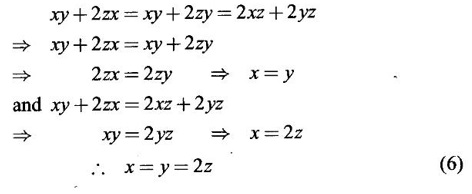
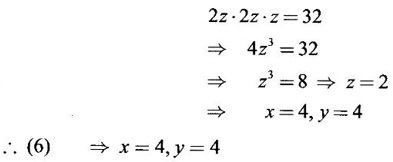

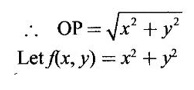
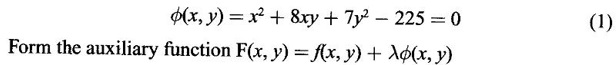
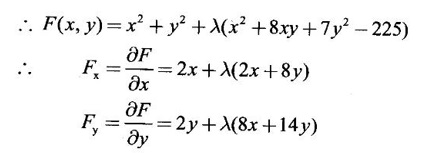

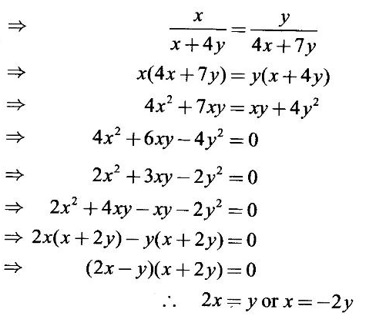
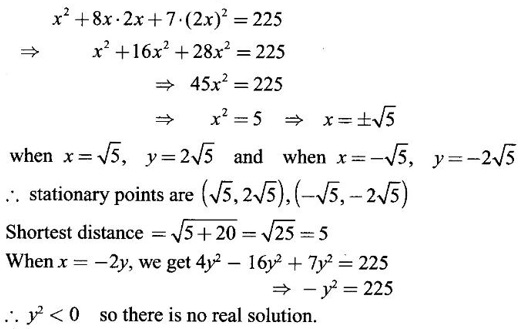

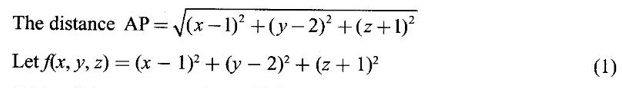
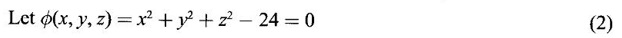
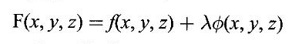
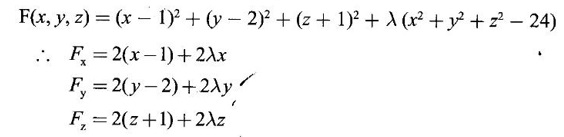


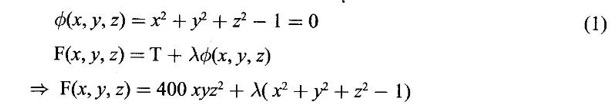
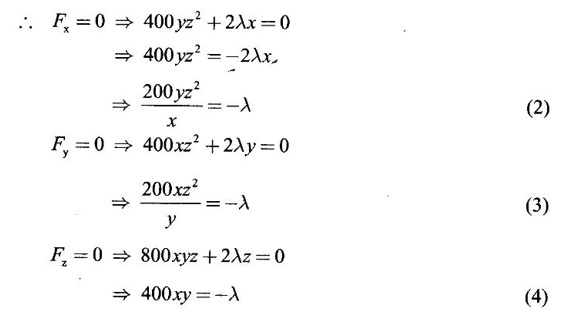


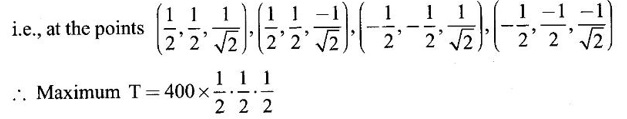
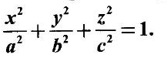
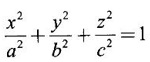
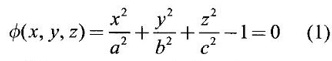
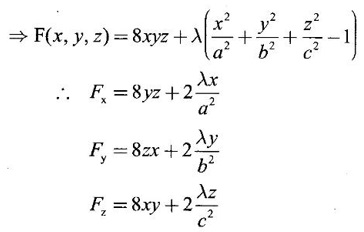

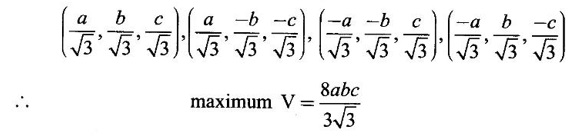
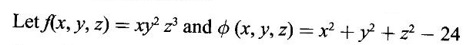
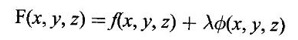
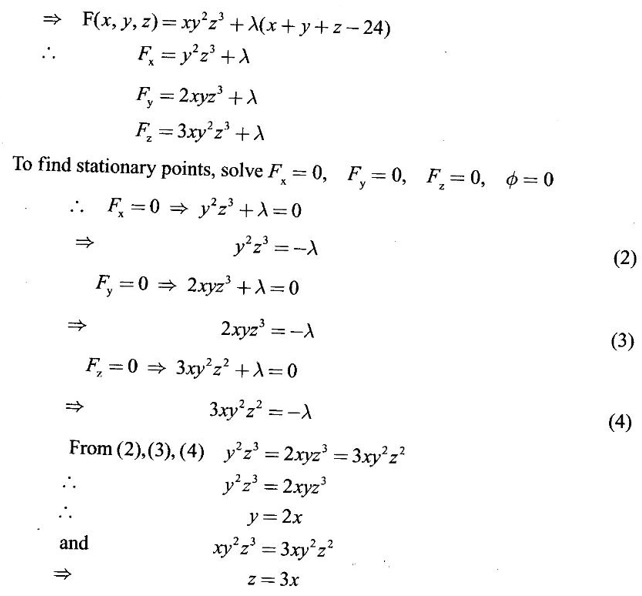
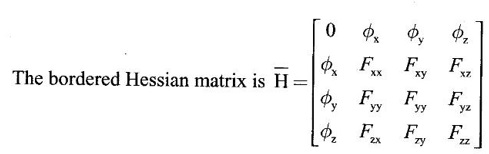
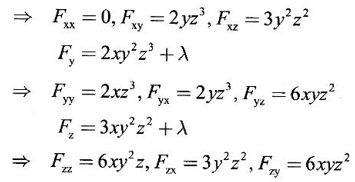

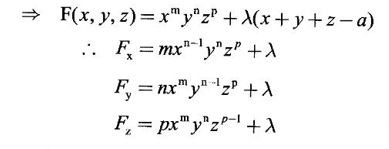
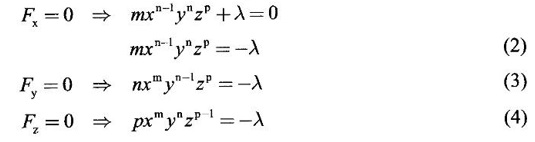

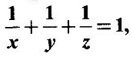 occurs at
occurs at 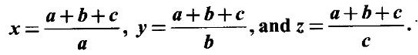

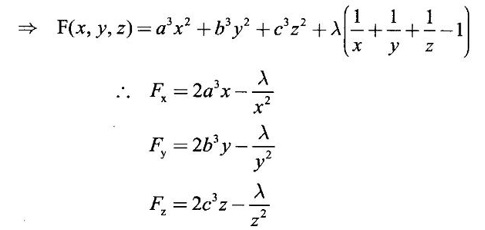

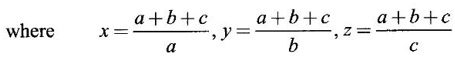
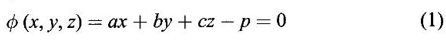
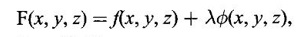
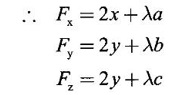


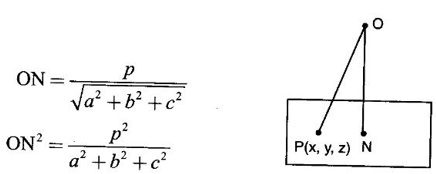
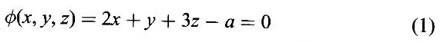
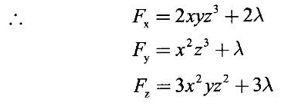
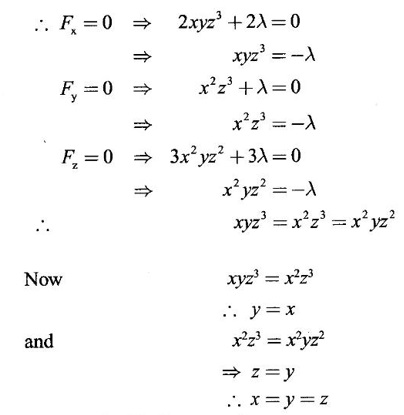

 is a maximum.
is a maximum. Required maximum value of u subject to xyz = 8.
Required maximum value of u subject to xyz = 8.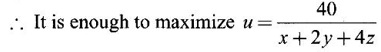
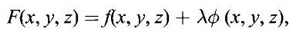
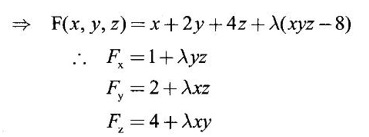
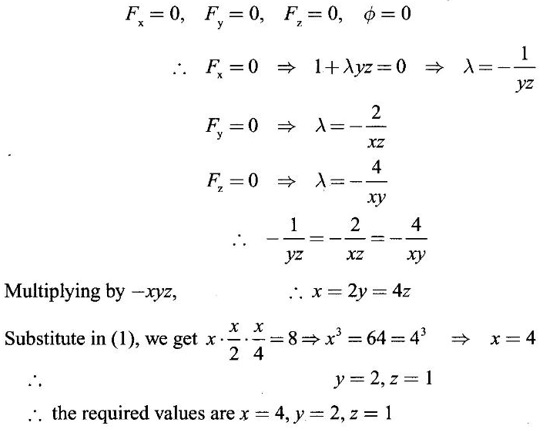
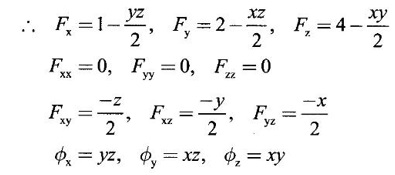
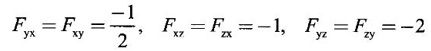

EXERCISE 3.5
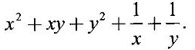
ANSWERS TO EXERCISE 3.5
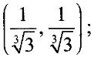
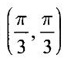 ; Maximum value
; Maximum value ![]()
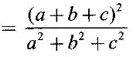
Matrices and Calculus: Unit III: Functions of Several Variables : Tag: : Definition, Worked Examples, Exercise with Answers - Applications: Maxima and Minima for Functions of Two Variables
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
