Matrices and Calculus: Unit I: Matrices
Application of Eigen Value Problem: Stretching of an Elastic Membrane
If the directions of X and Y are the same or opposite, then these directions are called Principal directions.
APPLICATION OF EIGEN VALUE PROBLEM: STRETCHING OF AN ELASTIC MEMBRANE If If m = 0, then Geometrically, If 3 Example 1 Thus Y = AX, which is a linear transformation. We can regard X as the position vector of the point P(x1, x2) and Y as the position vector of the point Q(y1, y2) in the xy-plane. The transformation Y = AX carries the point P into the point Q and For example, (i) If X = (x1, x2) = (1,1) then y1 = 5 × 1 + 3 × 1 = 8 and y2 = 3 × 1 + 5 × 1 = 8 ⸫ Y = (y1, y2) = (8,8) = 8(1,1) = 8X Hence X is stretched to Y in the same direction (ii) If X= (1, −1), then y1 = 5 × 1 + 3 × (-1) = 2 and y2 = 3 × 1 + 5 × (−1) = −2 ⸫ Y = (y1, y2) = (2, -2) = 2(1, -1) = 2X Hence X is stretched to Y in the same direction. (iii) If X = (2, 1), then y1 = 5.2 + 3.1 = 13 y2 = 3.2 + 5.1 = 11 ⸫ Y = (y1, y2) = (13, 11) So, Y ≠ m X for any real m Hence directions of X and Y are different. Note Suppose X = (1, 1) is stretched to Y = (-2, −2) by some transformation, then Y = -2 (1, 1) = -2X ⸫ X is stretched to Y in the opposite direction of X. Example 2 Consider an elastic membrane in the xy-plane. If a point P(x1, x2) lying on the boundary circle x2 + y2 = 1 is stretched to the point Q(y1, y2) by the transformation Y = AX, where A = Solution Solving (1) and (2) for x1 and x2, we get which represents an ellipse Note The general second degree equation ax2 + 2hxy + by2 + 2gx +2fy + c = 0 will represent an ellipse if h2 – ab < 0, a hyperbola if h2 – ab > 0, a parabola if h2 – ab = 0, and a circle if a = b and h = 0. In the equation (4) a = 34, h = -30, b = 34 ⸫ h2 – ab = (−30)2 – 34.34 = − 256 < 0 If the center of the ellipse is chosen as the origin and the major and the minor axis of the ellipse are chosen as the coordinate axes, then the ellipse reduces to canonical form or standard form Let P be a point in an elastic membarane in the xy plane with position vector X. Let P be pushed to a point Q in the plane with position vector Y by a linear transformation Y = AX, where A is 2 × 2 matrix. If the directions of X and Y are the same or opposite, then these directions are called Principal directions. In example 1, (i) Y= 8X and (ii) Y = 2X give principal directions, since the vector Y has the same direction as that of X. Since Y = AX, we have AX= 8X and AX = 2X. This means 8 and 2 are eigen values of A. Hence principal directions are related to eigen values of A.![]() is a vector and m is real number, then
is a vector and m is real number, then ![]() is a vector having the same direction as
is a vector having the same direction as ![]() if m> 0 and the opposite direction if m < 0.
if m> 0 and the opposite direction if m < 0.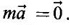
![]() stretches
stretches ![]() if m > 1, contacts if 0 < m < 1 and reverses if m < 0.
if m > 1, contacts if 0 < m < 1 and reverses if m < 0. then we write
then we write ![]() (x1, x2) which is the position vector of the point P(x1, x2).
(x1, x2) which is the position vector of the point P(x1, x2).![]() = (3x1, 3x2) is the position vector of the point Q(3x1, 3x2). Here 3
= (3x1, 3x2) is the position vector of the point Q(3x1, 3x2). Here 3![]() stretches
stretches ![]() in the same direction.
in the same direction.


 then find the curve on which Q lies.
then find the curve on which Q lies.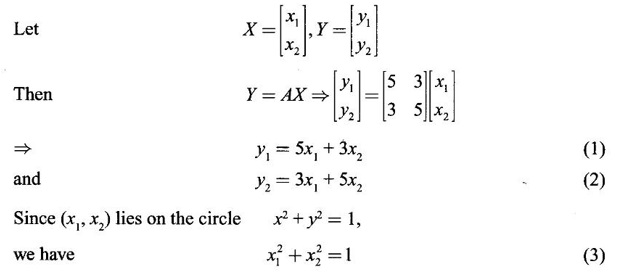

1. Principal Directions
Matrices and Calculus: Unit I: Matrices : Tag: : - Application of Eigen Value Problem: Stretching of an Elastic Membrane
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
