Strength of Materials: Unit III: Torsion
Anna University Solved Problems
Torsion - Strength of Materials
Anna University Solved Problems: Torsion - Strength of Materials
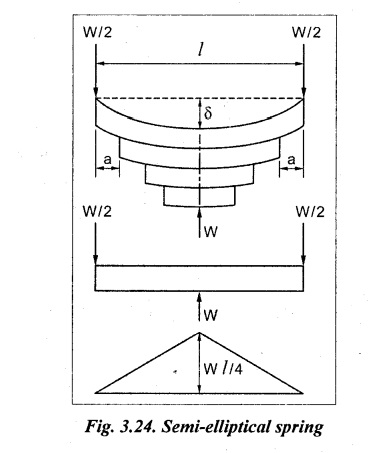
ANNA UNIVERSITY SOLVED PROBLEMS A close coiled helical spring of 5 mm diameter wire with has 16 coils of 100 mm inner diameter. If the maximum shear stress is limited to 150 Mpa. Find the stiffness of the spring. Take G = 85 Gpa. Given data: To find: Stiffness, K Solution: Result: Stiffness of the spring, K = 0.358 N/mm A close coil helical spring of round steel wire 10 mm in diameter has a mean radius of 120 mm. The spring has 10 complete turns and is subjected to an axial load of 200N. Determine (i) deflection of the spring (ii) maximum shear stress in the wire and (iii) stiffness of the spring. G = 80 kN/mm2. Given data: To find: (i) Deflection of the spring, ( δ ) (ii) Maximum shear stress in the wire, (τ) (iii) Stiffness of the spring, (K) Solution: Result: A closely coiled helical spring of round steel wire 5 mm in diameter having 12 complete coils of 50 mm mean diameter is subjected to an axial load of 100N. Find the deflection of the spring and maximum shearing stress in the material. Modulus of rigidity C = 80 kN/mm2. Given data: To find: δ and τ Solution: Result: (i) Deflection of spring, δ = 24 mm (ii) Maximum shear stress, τ = 101.86 N/mm2 A close.coiled helical spring made of steel wire is required to carry a load of 800N. Determine the wire diameter if the stiffness of the spring is 10 N/mm and the diameter of the helix is 80mm. Calculate the number of turns required in the spring. Given value for G for the steel is 80 Gpa and allowable stress is 200 N/mm2. Given data: To find: (i) Wire diameter (d) (ii) Number of turns required (n) Solution: We know that, Result: (i) Wire diameter, d = 9.34 mm (ii) Number of turns required, n = 15 A helical spring is equired to carry a total axial force of 50 N and to have a stiffness 0.4 N/mm. Design the spring using 6mm mild steel bar assuming its shear strength and rigidity modulus as 96 N/mm2 and 80 kN/mm2 respectively. Given data: To find: Design the spring Solution: We know that, Result: The mean diameter of the spring, D = 162.86 mm Number of turns required, n = 7.5 Deflection of the spring, δ = 125 mm Length of the spring, l = 3837.29 m A helical spring in which the mean diameter of the coil is 8 times the wire diameter is to be designed to absorb 0.2 kNm of energy with an extension of 100 mm. The maximum shear stress is not to exceed 125 N/mm2. Determine the mean diameter of the spring, diameter of the wire and the number of turns. Also find the load with which an extension of 40 mm could be produced in the spring. Assume G = 84 kN/mm2 Given data: To find: Solution: We know that, Result: An open coiled helical spring made of 5mm diameter wire has 16 coils 100 mm inner diameter with helix angle of 16° Calculate the deflection, maximum direct and shear stresses induced due to an axial load of 300 N. Take G = 90 Gpa and E – 200 Gpa. Given data: To find: Deflection, (δ) Maximum direct and shear stresses Solution: For open coiled helical spring, Result: This type of spring consists of number of leafs of steel plates of equal width and thickness but the length will be varying one below another held together at the centre by clamps. The leaf or carriage or laminated springs are used in cars, trains and wagons or lorries. These springs are supported at the centre and loaded at the ends. In this type of spring the friction between the plates are negligible. Example 3.71 A leaf spring is made of 12 steel plates of 50 mm wide and 5 mm thick. It carries a load of 4 kN at the centre. If the bending stress is limited to 140 N/mm2, determine the following: (a) Length of the spring (b) Deflection at the centre of the spring Take E = 2 × 105 N/mm2. Given: To find: Solution: We know that bending equation for semi-elliptical spring Result: (a) Length of the spring (l) = 350 mm (b) Deflection at the centre (δ) = 4.287 mm A leaf spring of semi-elliptical types has 10 plates, each 60 mm wide and 5 mm thick. The longest plate is 700 mm long. Find the greatest central load on the spring so that the bending stress shall not exceed 150 N/mm2 and the central deflection shall not exceed 10 mm. Take E = 2 × 105 N/mm2. Given: To find: Central load (W) Solution: (a) Bending stress consideration, (b) Deflection consideration, From the above consideration, for safe condition take lesser value. ⸫ Safe central load, W = 1.16 Kn Result: Central load (W) = 1.16 kN A carriage steel spring of semi-elliptical type has 1000 mm long and 50 mm width. It carries a central load of 5 kN. If the maximum deflection of the spring not exceed 50 mm and maximum stress should not exceed 150 N/mm2. Calculate the following; (a) The thickness of the plate (b) Number of plates Take E = 200 × 103 N/mm2. Given: To find: (a) Thickness of the plate (t) (b) Number of plates (n) Solution: We know that bending stress equation for semi-elliptical spring, Result: A quarter elliptical spring has a length of 1000 mm and consists of plates of each 40 mm wide and 10 mm thick. Find the least number of plates which can be used if deflection under gradually applied load of 4 kN is not to exceed 100 mm. Take E = 2 × 105 N/mm2. Given: To find: Number of plates (n) Solution: We know that the deflection equation for the quarter elliptical spring, Result: Number of plates (n) = 30 A laminated spring 1200 mm long has leaves of 100 mm wide and 10 mm thickness. The maximum bending stress 150 N/mm2 and the spring must absorb 100 Nm of energy when straightened. Calculate the number of leave and their initial radius of curvature. Take E = 2 × 105 N/mm2. Given: To find: Number of plates (n) Solution: We know that strain energy of the leaf spring, Result: Number of leaves (n) = 9Example 3.64


Example 3.65



Example 3.66

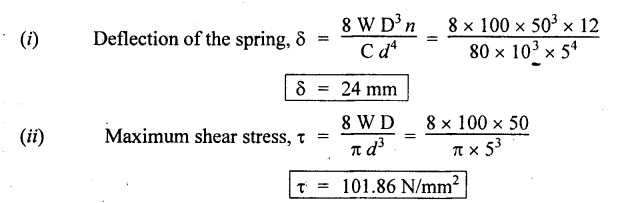
Example 3.67


Example 3.68


Example 3.69




Example 3.70


LEAF SPRING OR CARRIAGE SPRING OR LAMINATED SPRING
SEMI - ELLIPTICAL SPRING


QUARTER ELLIPTICAL SPRING OR CANTILEVER LEAF SPRING

SOLVED PROBLEMS ON LEAF SPRING


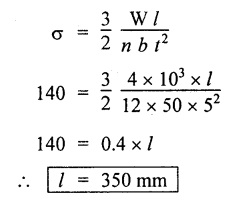
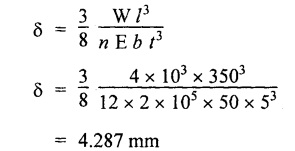
Example 3.72

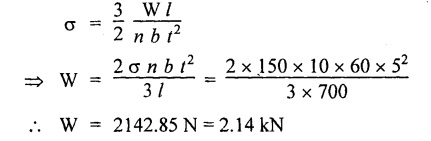
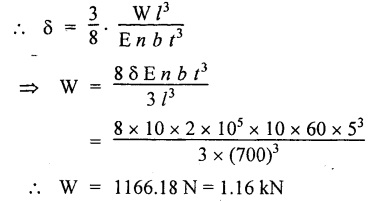
Example 3.73



Example 3.74

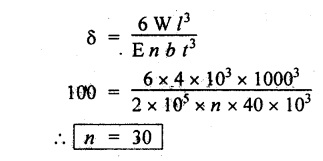
Example 3.75


Strength of Materials: Unit III: Torsion : Tag: : Torsion - Strength of Materials - Anna University Solved Problems
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
