Angular velocity ratio Theorem

ANGULAR VELOCITY RATIO THEOREM

• Theorem: The angular velocity ratio theorem states that the angular velocity ratio of two links relative to a third link is inversely proportional to the distances of their common instantaneous centre from their respective centres of rotation.

• Consider a four-bar mechanism and locate all the instantaneous centres, as shown in with angular velocity ω₂ in clockwise direction, then line velocity of the link 2 is given by

• Instead of ω₂, when ω₃ is given, then the velocity of link 2 is given by

• From equations (i) and (ii), it can be stated that the velocity of a link in a mechanism is equal to the product of the angular velocity and radius of instantaneous centre at that instant.

• The generalised equation to find the velocity of any link x is given by

• The angular velocity ratio for links 2 and 3 can be written from equation (i) and (ii) as

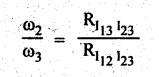
Now the generalized equation for angular velocity ratio is given by

Note

1. Centrode: The locus of all instantaneous centres is known as centrode.

2. Space centrode: The locus of the instantaneous centre in space during a definite motion of the body is called the space centrode.

3. Body centrode: The locus of instantaneous centre relative to the body itself is called the body centrode.

4. Instantaneous axis: A line drawn through an instantaneous centre and perpendicular to the plane of motion is called instantaneous axis.

5. Axode: The locus of instantaneous axis is known as axode.