Theory of Machines: Unit I: Kinematics of Mechanisms
analytical method for velocity and acceleration of slider- crank mechanism
Kinematics of Mechanisms - Theory of Machines
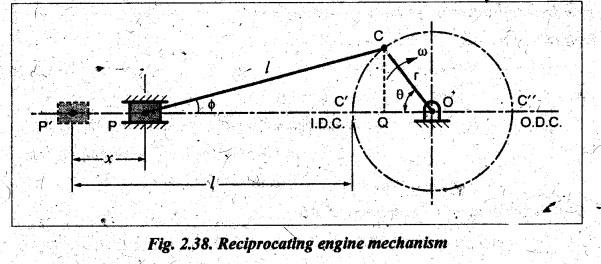
Consider a reciprocating steam engine mechanism OCP as shown in Fig.2.38.
ANALYTICAL METHOD FOR VELOCITY AND ACCELERATION OF SLIDER- CRANK
MECHANISM
Consider
a reciprocating steam engine mechanism OCP as shown in Fig.2.38. Let crank OC
rotates with angular velocity o rad/s and the connecting rod PC makes angle
with the line of stroke PO. Let x be the displacement of piston from
initial point P' to P, when the crank turns through an angle θ from I.D.C.
Let
r
= Crank radius,
l
= Length of the connecting rod,
θ
= Angle made crank with I.D.C.,
ϕ
= Inclination of connecting rod to the line of stroke PO, and
n
= l/r = Ratio of length of connecting rod to the radius of crank,
also known as obliquity ratio.
1. Velocity of the Piston (VP)
From
the geometry of Fig.2.38, displacement of the piston is given by
x
= P'P = OP' - OP= (P'C' +C'O) – (PQ +
QO)
From
∆CPQ, PQ = l cos ϕ and from ∆COQ, QO = r cos θ
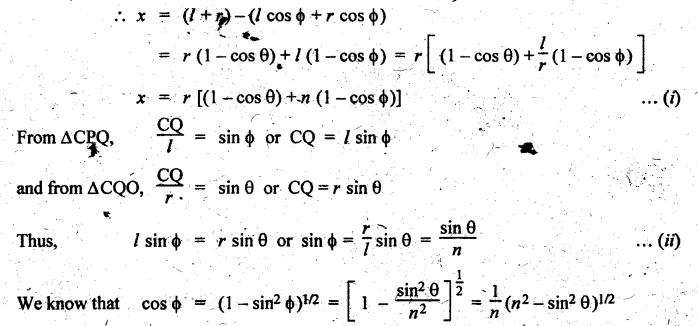
By
expanding the above expression by binomial theorem, we get
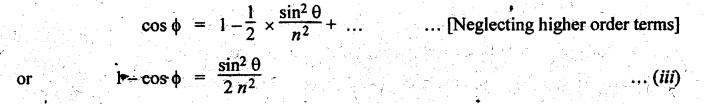
Substituting
equation (iii) in equation (1), we get

Differentiating
equation (2.20) with respect to θ, we get
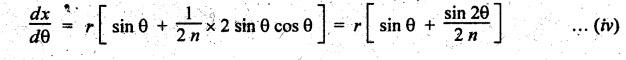
Therefore,
velocity of the piston or velocity of P with respect to O,
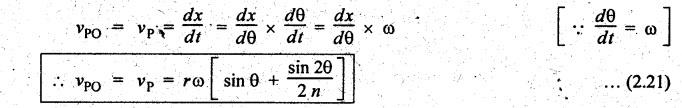
2 Acceleration of the Piston (aP)
We
know that acceleration is the rate of change of velocity. So, acceleration of
the piston P is given by
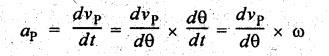
Differentiating
equation (2.21) with respect to θ, we get
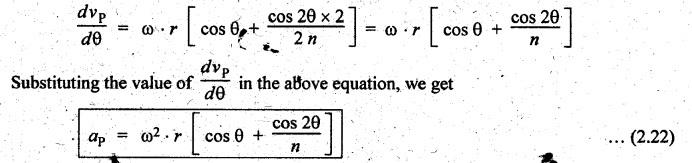
Note
1.
If the value of n is very large, then aP = ω2r
cos θ, as in case of SHM.

As
the direction of motion is reversed at the outer dead centre (ODC) position, therefore,
changing the sign of the above expression, we get
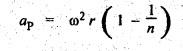
3. Angular Velocity of the Connecting Rod (ωPC)
From
the geometry of the Fig.2.38, we find that

Differentiating
both sides with respect to time t, we get
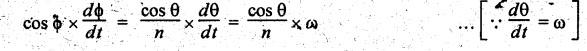
Since
the angular velocity of the connecting rod PC is same as the angular velocity
of point P with respect to C and is equal to dϕ/dt, therefore
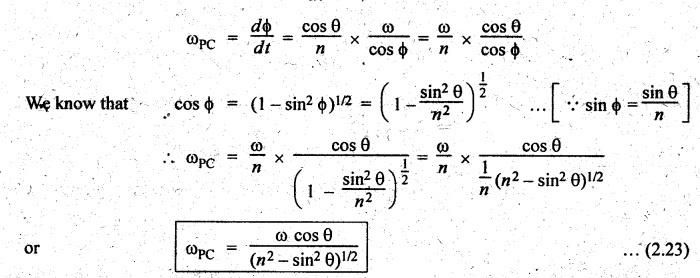
4. Angular Acceleration of the Connecting Rod (αPC)
We
know that the angular acceleration of P with respect to C,
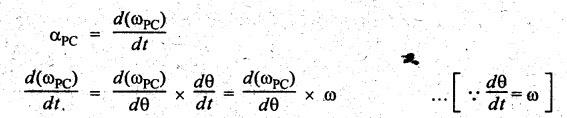
Differentiating
equation (2.23) with respect to θ, we get
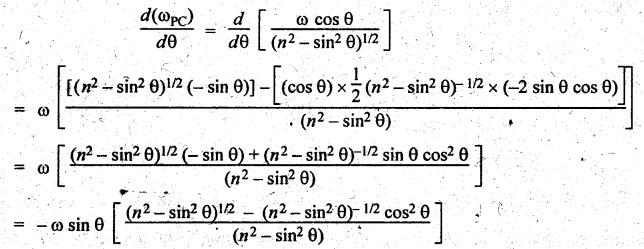
Dividing
and multiplying by (n2 - sin2 θ)1/2, we
get
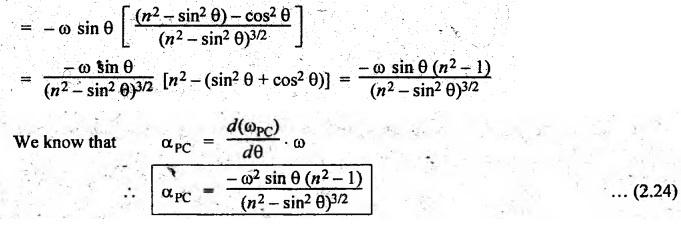
The
negative sign indicates that the sense of angular acceleration of the rod is
such that it tends to reduce the angle ϕ.
Note
1.
Since sin2 θ is small as compared to n2, therefore
it may be neglected. Thus equations (2.23) and (2.24) are reduced to
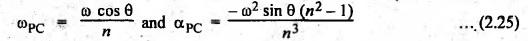
2.
Also in equation (2.25), unity is small as compared to n2,
hence the term unity can be neglected.

Example 2.14
The lengths of crank and connecting rod of a horizontal
reciprocating engine are 125 mm and 500 mm respectively. The crank is rotating
at 600. rpm. When the crank has turned 45°from inner dead centre, find
analytically,
(i) the velocity and acceleration of the slider,
(ii) the angular velocity, and angular acceleration of the
connecting rod.
Given data.
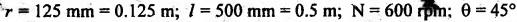
Solution:
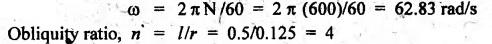
(i)
Velocity and acceleration of the slider (vP and aP):
Velocity
of the slider is given by
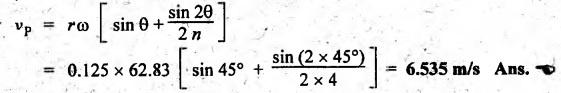
Acceleration
of the slider is given by
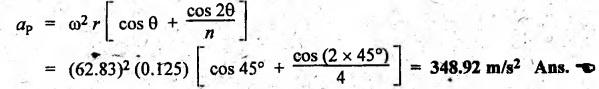
(ii)
Angular velocity and angular acceleration of the connecting rod (ωPC
and αPC):
Angular
velocity of the connecting rod is given by
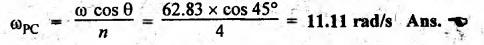
Angular
acceleration of the connecting rod is given by
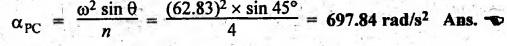
Example 2.15
In a reciprocating engine mechanism, the lengths of the crank
and connecting rod are 150 mm and 600 mm respectively. The crank position is
45°from inner dead centre. The crank-shaft speed is 300 rpm (clockwise). Using
analytical method, determine:
(i) the velocity of the piston;
(ii) the acceleration of the piston; and
(iii) the crank angle for maximum velocity of the piston and the
corresponding velocity.
[A.U.,
Nov/Dec 2012]
Given data:
r
= 150 mm 0.15 m; l = 600 mm = 0.6 m; N = 300 rpm; θ = 45°
Solution:
ω =
2πN/60 = 2 π (300)/60 = 31.41 rad/s
Obliquity
ratio, = l/r = 0.6/0.15 = 4
(i)
Velocity of the piston (vP):
Velocity
of the piston is given by
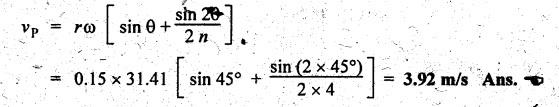
(ii)
Acceleration of the piston (aP):
Acceleration
of the slider is given by
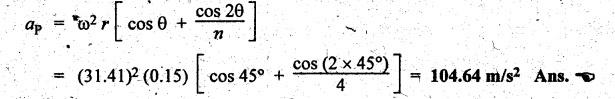
(iii)
Crank angle for maximum velocity of the piston the corresponding velocity:
Let
θ
= Crank angle from IDC at which the
maximum velocity occurs
We
know that the velocity of the piston,
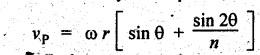
For
maximum velocity of the piston,
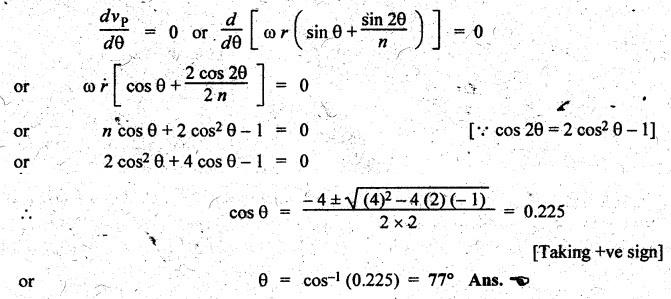
Substituting
the value θ = 77° in the vP equation, we get
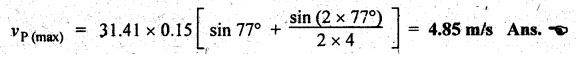
Example 2.16
In a simple steam engine, the lengths of the crank and the
connecting rod are 100 mm and 400 mm respectively. The weight of the connecting
rod is 50 kg and its centre of mass is 220 mm, from the cross-head centre. The
radius of gyration about the centre of mass is 120 mm. If the engine speed is
300 rpm and the crank has turned 45° from IDC, determine:
(i) the angular velocity and angular acceleration of the
connecting rod; and
(ii) the kinetic energy of the connecting rod.
Given data:
r
= 100 mm = 0.1 m; l = 400 mm = 0.4 m; m = 50 kg; k = 120
mm = 0.12 m; N = 300 rpm; θ = 45°
Solution:
ω
= 2πN/60 = 2 π (300)/60 = 31.4
rad/s
Obliquity
ratio, n = l/r = 0.4/0.1 = 4
(i)
Angular velocity and angular acceleration of the connecting rod (ωPC
and αPC):
Angular
velocity of the connecting rod is given by
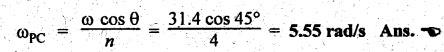
Angular
acceleration of the connecting rod is given by
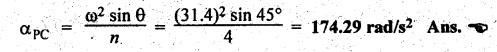
(ii)
Kinetic energy of the connecting rod:
We
know that the kinetic energy of the connecting rod,
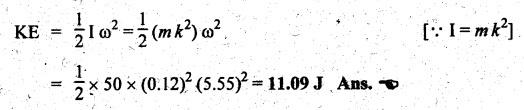
Theory of Machines: Unit I: Kinematics of Mechanisms : Tag: : Kinematics of Mechanisms - Theory of Machines - analytical method for velocity and acceleration of slider- crank mechanism
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
