Acceleration of a rigid link

II. ACCELERATION ANALYSIS BY RELATIVE ACCELERATION METHOD

ACCELERATION OF A RIGID LINK

• We know that acceleration is the rate of change with respect to time.

• Like velocity, acceleration is also a vector quantity as it has both magnitude and direction.

• Consider a link AB rotating about point A in clockwise direction, as shown in Fig.2.12(a). Let ω be the angular velocity and a be the angular acceleration of point B with respect to A.

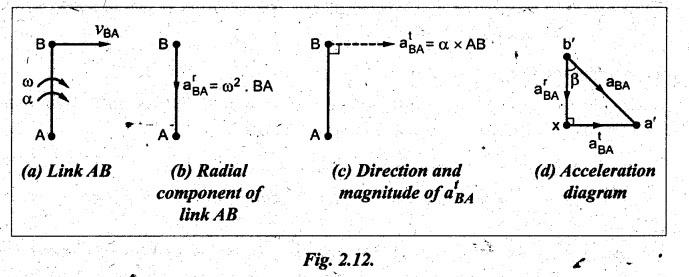
• As discussed already, the velocity of point B with respect to A (v_BA) is always perpendicular to the link AB, as shown in Fig.2.12(a).

1. Components of Acceleration

Since the velocity of a particle changes in both magnitude and direction, therefore it has two components of acceleration.

1. Radial (or centripetal) component, and

2. Tangential component.

1. Radial (or Centripetal) Component (a^r_BA):

• The radial or centripetal component of acceleration acts in the direction parallel to the link and its direction is towards the centre of rotation, as shown in Fig.2.12(b).

• Magnitude: The magnitude of the radial component of acceleration of link AB is given by

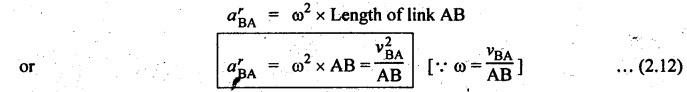
• Direction: The direction of a^r_BA is towards the centre of rotation A, as shown in Fig.2.12(b). In other words, it acts perpendicular to the velocity of link AB.

2. Tangential Component (a^t_BA):

• The tangential component of acceleration acts in the direction perpendicular to the link, as shown in Fig.2.12(c).

• Magnitude: The magnitude of the tangential component of acceleration of link AB is given by

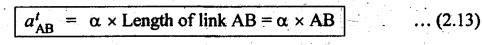
• Direction: The direction of a^t_AB is perpendicular to link AB, as shown in Fig.2.12(c). In other words, it acts parallel to the velocity of link AB, v_BA.

Total Acceleration, a_BA:

• The total acceleration of point B with respect to A is the vector sum of its radial component and tangential component, as shown in Fig.2.12(d).

Note

1. If a link rotates at a constant angular velocity, then the tangential component of acceleration a' becomes zero.

2. If a link (like slider/piston) moves in a straight line, then the radial component of acceleration a^r becomes zero. This is because the straight line motion may be assumed as rotational motion having infinite radius; so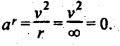 

2. Acceleration Image of a Link

The acceleration diagram of a link AB can be drawn as shown in Fig.2.12(d), using the following procedure.

1. From any arbitrary point b', draw vector b'x such that b'x' = a^r_BA in the direction parallel to BA (from B to A) to represent the radial component of B with respect to A (i.e., a^r_BA).

2. Now from point x₂ draw vector xa' such that a^t_BA in the direction perpendicular to BA to represent the tangential component of B with respect to A (i.e., a^t_BA).

3. Join points a' and b' to obtain vector b'a'. The vector b'a' represents the total acceleration of B with respect to A (i.e., a_BA). The vector b'a' is known as the acceleration image of link AB.